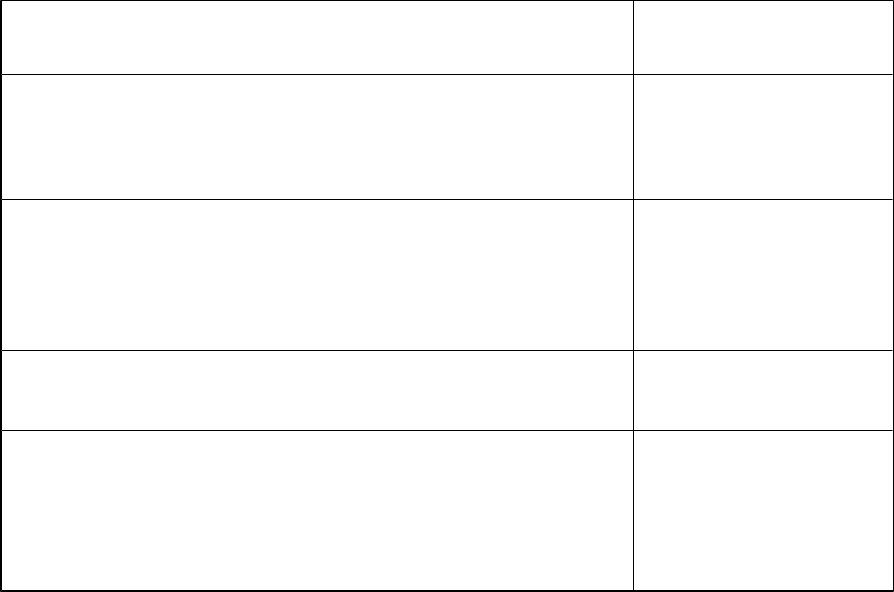
Логическая |
Названия логической |
Обозначение |
связка |
операции |
|
Не |
Отрицание, инверсия |
‾ |
¬ |
|
|
||
И, а, но, хотя |
Конъюнкция = логическое |
|
|
|
умножение |
|
|
|
|
& |
^ |
Или |
Дизъюнкция = логическое |
|
|
|
сложение |
V |
+ |
Если …то |
Импликация = следование |
|
|
Тогда и только |
Эквивалентность(эквиваленция)= |
≡ |
~ |
тогда, когда |
равнозначность |
|
|
Порядок выполнения операций:
1.Операции в скобках
2.Отрицание
3.Конъюнкция
4.Дизъюнкция
5.Импликация
6.Эквивалентность
ПРИМЕР 1: А V (B C) D ↔ ¬ A
1.В С - импликация
2.¬ А - инверсия
3.(В С) D - конъюнкция
4.А V (B C) D - дизъюнкция
5.А V (B C) D ↔ ¬ A - эквивалентность
Запомни!
СВОЙСТВА ЛОГИЧЕСКИХ ФУНКЦИЙ
Инверсия истинна
Дизъюнкция ложна
------------------------------
Конъюнкция истинна
Дизъюнкция истинна
------------------------------
Конъюнкция ложна
Импликация ложна
Эквивалентность истинна
Т
О
Г
Д
А
И
Т
О
Л
Ь
К
О
Т
О
Г
Д
А,
К
О
Г
Д
А
высказывание ложно
ложные
оба высказывания -------------
истинные
Истинно хотя бы одно
высказывание --
ложно
из истинного следует
ложное высказывание
оба высказывания ложны
или оба высказывания истинны
Алгоритм построения таблицы истинности логической формулы:
1.подсчитать количество переменных в формуле;
2.определить число строк в таблице m = 2^n, где n –количество переменных;
3.подсчитать количество логических операций в формуле;
4.установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5.определить количество столбцов в таблице: число переменных + число операций;
6.выписать наборы значений переменных в виде последовательности возрастающих n-разрядных двоичных чисел от 0 до (2^n – 1);
7.провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в п.4 очередностью выполнения
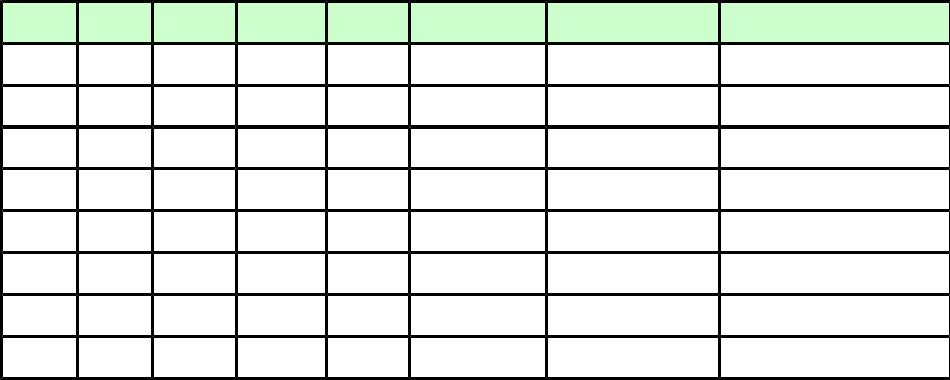
Пример: Для формулы А & (B v ¬ B & ¬ C)
построить таблицу истинности
А |
В |
С |
¬B |
¬С |
¬В&¬C |
Bv(¬B&¬C) |
A& (B v¬B&¬C) |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
Задача: Пусть a, b, c – логические величины, которые имеют следующие значения: a = истина, b = ложь, c = истина. Определите результаты вычисления следующих логических выражений:
1. |
a ^ b |
1 ^ 0 = 0 |
2. |
a v b |
1 v 0 = 1 |
3. |
¬a v b ^ c |
¬1 v 0 ^ 1 = 0 v 0 ^ 1 = 0 v 0 = 0 |
4. |
¬(a v b) ^ (c v b) |
¬(1v0) ^ (1v0) = ¬1 ^ 1 = 0 ^ 1 = 0 |
|
|
|
Задача: Пусть a, b, c – логические величины, которые имеют следующие значения: a = истина, b = ложь, c = истина. Определите результаты вычисления следующих логических выражений:
Вариант 1:
b ^ c ¬a v b
a ^ b v c ¬(a ^ b ^ c) (a ^ b) v (b ^ c)
Вариант 2:
b v c ¬a ^ b
a v b ^ c ¬(a v b v c) (a v b) ^ (b v c)
Пример. Построим таблицу истинности следующей функции:
Порядок действий: F (A, B,C) A (C B) 1. Количество строк в таблице Q=2n, где n - количество
переменных (аргументов), здесь n = 3 (А, В, С) и тогда Q=23=8
2. Количество столбцов = число переменных + число операций
(здесь 3+3=6 столбцов)
3. Выписать наборы входных переменных. Это удобнее сделать так:
a)разделить колонку значений первой переменной пополам и заполнить верхнюю половину 0, нижнюю половину 1.
b)разделить колонку значений второй переменной на 4 части и заполнить каждую четверть чередующимися группами 0 и 1 , начиная опять с группы 0.
c)продолжить деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами из 0
или 1 до тех пор, пока группы 0 и 1 не будут состоять из одного символа. (Можно заполнять все колонки, начиная с группы
единиц.)
4. Провести заполнение таблицы истинности по столбикам, выполняя логические операции.
Построим таблицу истинности для следующей
функции: |
F(A, B,C) A ( |
|
|
|
B) |
|
|
||||
C |
|
|
|||||||||
A B C |
|
|
|
B A ( |
|
B) |
|||||
|
|
|
C |
||||||||
С |
С |
||||||||||
0 |
0 |
0 |
1 |
|
0 |
0 |
|||||
0 |
0 |
1 |
0 |
|
0 |
0 |
|||||
0 |
1 |
0 |
1 |
|
1 |
1 |
|||||
0 |
1 |
1 |
0 |
|
0 |
0 |
|||||
1 |
0 |
0 |
1 |
|
0 |
1 |
|||||
1 |
0 |
1 |
0 |
|
0 |
1 |
|||||
1 |
1 |
0 |
1 |
|
1 |
1 |
|||||
1 |
1 |
1 |
0 |
|
0 |
1 |
|||||
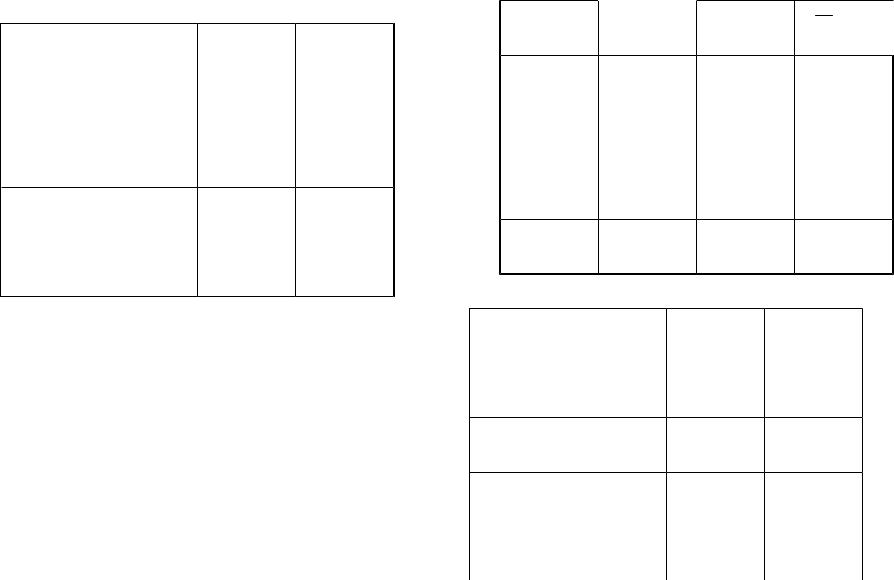
Задание. Построить таблицу истинности для следующих функций:
|
|
|
|
F |
|
B |
||||||
1) |
F A B |
|
2) |
A |
||||||||
А |
B |
|
|
|
|
|
А |
B |
|
|
А |
|
|
А A B |
|||||||||||
|
0 |
0 |
1 |
|||||||||
0 |
0 |
1 |
|
|
1 |
|||||||
|
|
0 |
1 |
1 |
||||||||
0 |
1 |
1 |
|
|
1 |
|||||||
|
|
1 |
0 |
0 |
|
|||||||
1 |
0 |
0 |
|
|
0 |
|
||||||
|
|
1 |
1 |
0 |
||||||||
1 |
1 |
0 |
|
|
1 |
|||||||
|
|
|
|
|
|
|
|
|||||
A B 
0
1
0
0
|
|
|
|
А |
B |
A |
B ( |
A B |
) |
|
3) |
F (A B) |
|||||||||
0 |
0 |
0 |
1 |
|
||||||
|
|
|
|
|
||||||
|
|
|
|
0 |
1 |
1 |
0 |
|
||
|
|
|
|
1 |
0 |
1 |
0 |
|
||
|
|
|
|
1 |
1 |
1 |
0 |
|
||