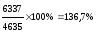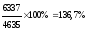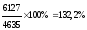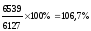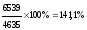1.2.2. Относительный показатель динамики (опд)

Относительный показатель динамики (ОПД) – это отношение уровня исследуемого или явления за определенный период времени (на данный момент времени или в прошлом). Определяется по формуле:

В статистике различают относительные показатели динамики с постоянной и переменной базой сравнения. Если сравнение осуществляется с одним и тем же базисным уровнем, то получают базисные ОПД. При расчете ОПД с переменной базой получают цепные ОПД.

Исходные данные о стоимости земельных участков в N-ом районе, Московской области (пойма реки Протва, 85 км. от МКАД), в 2004 – 2007 гг. представлены в таблице 1.1.

Таблица 1.1

Стоимость земельных участков в N - ом районе Московской области

Год Показатель	2004	2005	2006	2007
Стоимость земельного участка за 1 сот., усл.ед.	4635	6337	6127	6539

Пример расчета относительных показатели динамики с переменной и постоянной базой сравнения представлен в таблице 1.2. Относительные показатели динамики с переменной и постоянной базой сравнения взаимосвязаны между собой: произведение всех относительных показателей с переменной базой равно относительному показателю с постоянной базой сравнения за исследуемый период.

Таблица 1.2

Относительные показатели динамики с переменной и постоянной базой сравнения

Цепные показатели	Базисные показатели

Для рассчитанных показателей, переведенных из процентов в коэффициенты, получим:

1,367 • 0,967 • 1,067 = 1,411 = 141,1% (стоимость земельных участков за 4 года возросла на 41,1%).

1.2.3. Средняя арифметическая взвешенная

На конец 2007 года размеры земельных участков, предоставленных для ведения крестьянского (фермерского) хозяйства (К(Ф)Х) в Российской Федерации, характеризуются данными таблицы 1.3.

Таблица 1.3

Земельные участки крестьянских (фермерских) хозяйств

№ п.п	Размер земельного участка, га	Удельный вес в общем числе хозяйств, %
1	до 3	18,0
2	4 - 6	9,7
3	7 - 11	13,9
4	12 - 18	15,5
5	19 - 49	18,7
6	50 - 70	6,0
7	71 - 101	5,7
8	102 - 200	7,0
9	свыше 200	5,5
10	Итого	100,0

Используя исходные данные (по вариантам) определяем средний размер земельного участка, предоставленный для ведения К(Ф)Х, соблюдая следующую последовательность действий:

1. Записываем исходное логическое соотношение для данной средней:

2. Обозначаем значение усредняемого признака (размер земельного участка) через X, а частоту повторения данного признака (количество К(Ф)Х) через f.

3. Так как значения усредняемого признака заданы в виде интервалов, то найдем их середины, т.е. 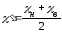. При этом величину первого интервала условно приравняем к величине второго, тогда его нижняя граница будет равна 1 га. Величину последнего интервала условно приравняем к величине предпоследнего, тогда его верхняя граница составит 299 га. В результате получаем следующие середины интервалов ():

2 га, 5 га, 9 га, 15 га, 34 га, 60 га, 86 га, 151 га, 249 га.

4. Роль числа К(Ф)Х в данном случае выполняет их доля в общем итоге, выраженная в процентах. Для расчета воспользуемся формулой средней арифметической взвешенной:

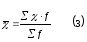
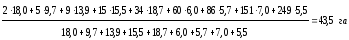
По результатам расчета - средний размер К(Ф)Х в РФ равен 43,5 га. На рисунке 1.1 представлена кольцевая диаграмма распределения земельных участков К(Ф)Х, которая позволяет наглядно отобразить результаты проведенных расчетов. Из данной диаграммы видно, что наибольший удельный вес (18%) занимают земельные участка площадью от 19 до 49 га. Участки площадью 50-70 га, 71-101 га и свыше 200 га занимают наименьший удельный вес (6%).

Рис. 1.1. Кольцевая диаграмма распределения земельных участков К(Ф)Х

После изучения параграфов 1.2.1-1.2.3 студент сможет:

- объяснить сущность и значение абсолютных и относительных величин, а также их применение по видам и формам выражения;

- обосновать выбор формулы средней величины;

- раскрыть содержание и особенности расчета средних величин разных видов;

- объяснить свойства и значение средней арифметической как наиболее распространенной в статистике.