3. Случайные сигналы и шумы
3.1 Математический аппарат случайных сигналов
Раздел
математики - теория вероятности, исследует
случайные процессы. Отличительной
чертой случайного процесса является
то, что его значения (например: напряжение
или ток) нельзя заранее предсказать.
Поэтому, когда говорят о конкретной
величине какого-нибудь случайного
процесса (например: напряжение на зажимах
разогретого до температуры
резистора), то подразумевают его
статистическую характеристику.
В теории вероятностей введены понятия:
-
функции распределения случайной величины
,
т.е. вероятность того, что случайная
величина
из множества
примет значение, равное или меньшее чем
.
Для функции распределения справедливы два предельных равенства:
(3.1)
- производная от функции распределения - есть плотность вероятности:
. (3.2)
Плотность вероятности удовлетворяет условию нормировки,
т.е.
(3.3)
Для
случайных величин
из множества
введены понятия:
-
Математическое ожидание ( m ) - среднее значение, которое может принимать случайная величина
:
(3.4)
-
Дисперсия или среднеквадратичное отклонение
,
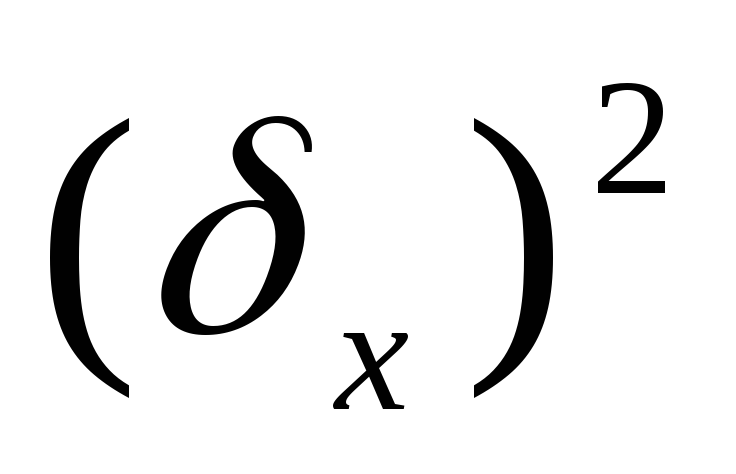которое характеризует меру разброса
результатов испытаний относительно
математического ожидания.
(3.5)
Пример 1 Равномерное распределение.
Пусть
случайная величина
может принимать значения из интервала
,
причем вероятности попадания в любые
внутренние интервалы равны.
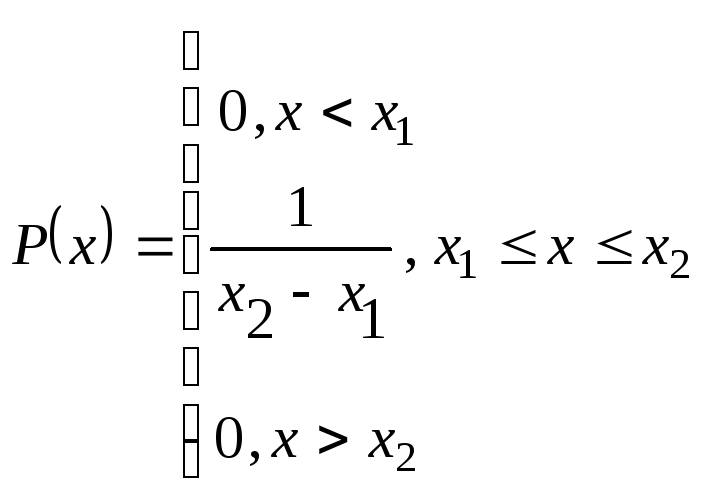
Функцию распределения находят путем интегрирования плотности вероятности.
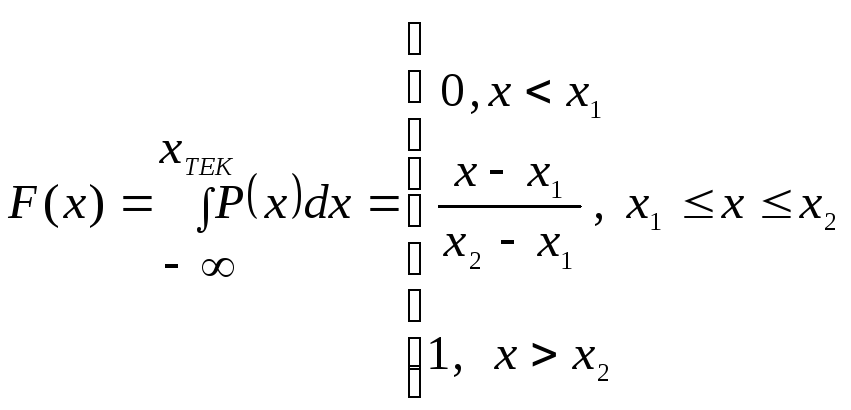
График плотности вероятности и функции распределения показан на рис.3.1.
Математическое ожидание:
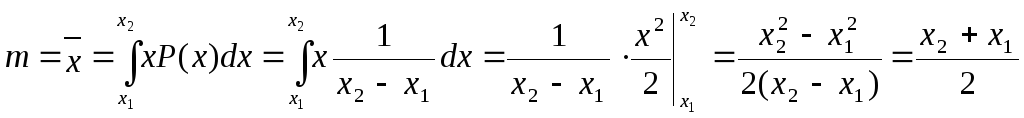
Дисперсия:
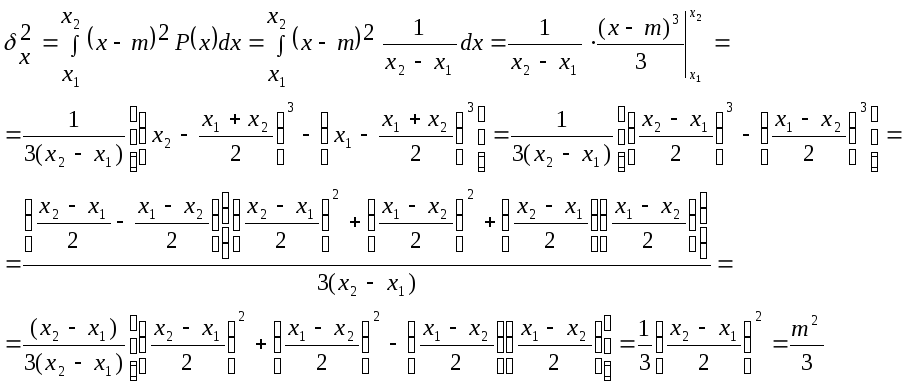
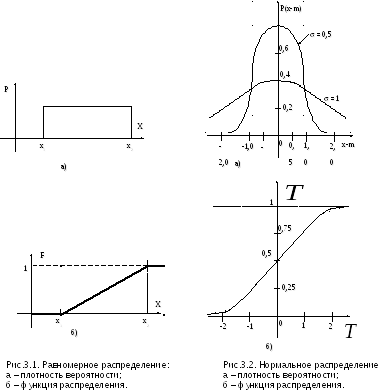
Пример 2: Гауссово (нормальное) распределение.
Плотность
вероятности Гауссового распределения
(рис.3.2),
,
содержит два параметра
.
и
.
График данной функции представляет
собой колоколообразную кривую с
максимумом в точке
.
Непосредственным
вычислениями можно показать, что
есть математическое ожидание, а
есть
среднеквадратичное отклонение
.
Тогда плотность вероятности записывается
в виде:
Функция распределения имеет вид:
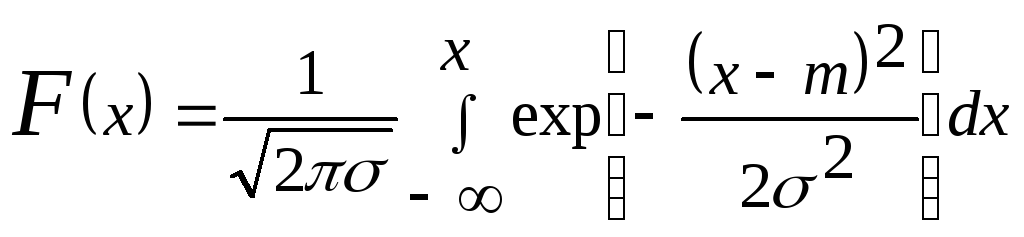
График этого распределения приведен на рис.3.2.
К случайным процессам также относятся флуктуации напряжения и тока, связанные с шумовыми явлениями в полупроводниковых приборах. Шумы определяют нижнюю границу величины электрического сигнала, который необходимо усиливать или преобразовывать с помощью полупроводниковых приборов. Поэтому необходимо знать величину и природу шумовых явлений.
3.2 Тепловой шум в резисторе (шум Джонсона )
Причиной возникновения теплового шума являются флуктуации носителей заряда в проводящих телах под действием температуры. Это могут быть резисторы или проводники в виде металлической (Al, Au, Cr, W, V) пленки, используемой в ИМС, а также пленки или объемы полупроводниковых структур. Спектр шумового напряжения теплового шума очень широк из‑за высокой плотности упаковки и высокой скорости носителей заряда.
Среднеквадратичное отклонение напряжения теплового шума резистора связано с величиной его сопротивления R выражением Джонсона - Найквиста:
, (3.6)
где
- сопротивление
резистора;
Дж/K - постоянная Больцмана,
Дж
при
;
- полоса
пропускания, в которой измеряется шум.
Cпектральная плотность среднеквадратичного отклонения напряжения теплового шума составит:
(3.7)
Пример
1. При
и
спектральная плотность напряжения
теплового шума составит
.
Найти чему равно шумовое напряжение.
Решение:
Формула (3.6) для среднеквадратичного отклонения тока теплового шума резистора имеет вид:
(3.6а)
или для спектральной плотности среднеквадратичного отклонения шумового тока:
(3.7а)
Аналогичный
расчет для
и
показывает, что величина шумового тока
составит:
Эквивалентная схема резисторов соответствующих выражениям (3.6) и (3.6а) имеют вид, показанный на рис.3.3.
Ш
умовые
источники на эквивалентных схемах
обычно заштриховывают.
Источником дробового шума в полупроводниках является упорядоченное (под действием электрического поля) перемещение носителей, имеющих разную энергию. Проявляется он, например, в диодах или транзисторах, при прохождении носителями потенциального барьера.
Рассмотрим простую модель дробового шума. Пусть роль потенциального барьера выполняет p-n переход. Предположим, что концентрация электронов существенно превосходит концентрацию дырок. Тогда ток через p-n переход будет определяться потоком электронов как
,
где
-
полный заряд, перенесенный электронами;
- интервал времени переноса заряда через
p‑n переход.
Для
единичного электрона этот ток
можно приблизительно рассчитать
следующим образом:
,
где
[кулон]
- заряд электрона;
[сек]
- время пролета через p-n переход.
Обычно ток через p-n переход составляет несколько миллиампер. Это означает, что единичные вклады тока от отдельных электронов перекрываются во времени (рис.3.4).
Каждый электрон, движущийся в этом направлении, может иметь разную скорость, следовательно, и разную энергию. Это означает, что не все электроны преодолевают потенциальный барьер p-n перехода, а только те, энергия которых больше величины .
Хаотический шум, возникающий при преодолении потенциального барьера, называется дробовым. Среднеквадратичное отклонение дробового шума определяется выражением Шоттки :
, (3.8)
где
- величина
заряда носителей;
- ток
через соответствующий полупроводниковый
прибор;
- частотная
полоса пропускания, в которой измеряется
шум.
Спектральная плотность шума Шоттки имеет вид
(3.9)
Э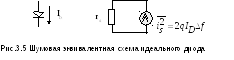
квивалентная
схема идеального диода с p-n
переходом, содержащая дробовой шум,
имеет вид показанный на рис.3.5, где
- дифференциальное сопротивление диода.
Следует отметить, что спектральные плотности теплового и дробового шума не зависят от частоты. Шум такого типа называется белым шумом. Спектр частот белого шума бесконечен.