Занятие 15. Системы линейных однородных дифференциальных уравнений 1-го порядка с постоянными коэффициентами: общее и частное решения.
|
Ауд. |
Л-2, Гл. 10 |
№ 432, 434, 436, 438, 440. |
5 |
☺ ☻ ☺
Общие
сведения. Учитывая, что трудоёмкость
решения систем дифференциальных
уравнений существенно зависит от числа
функций, участвующих в построении
системы, в предлагаемых для самостоятельных
упражнений заданиях мы ограничиваемся
системами, состоящими из двух уравнений.
Поэтому все общие выражения, применяемые
при решении систем уравнений, относим
только к системам двух дифференциальных
уравнений:
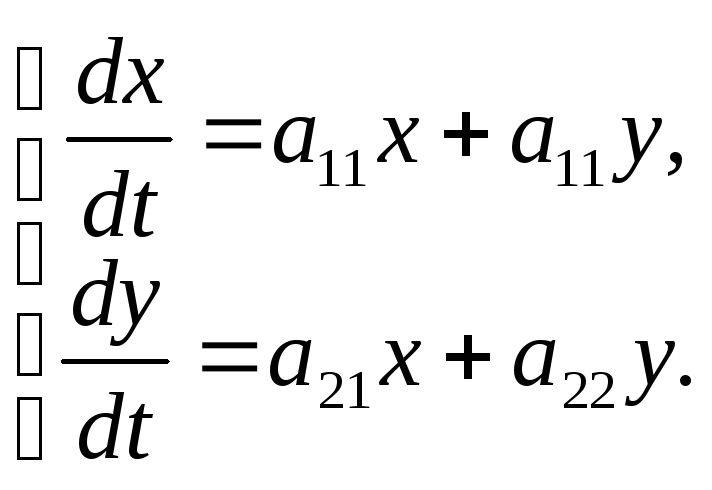(1)
где
–
действительные числа (постоянные);
,
– искомые, дифференцируемые функции.
Замечание: при ссылках на отдельные уравнения системы будем использовать двухпозиционные записи; например: (1.1) – ссылка на 1-е уравнение системы (1).
Решение системы
уравнений подсказывает равносильность
системы (1) линейному дифференциальному
уравнению 2-го порядка с постоянными
коэффициентами для любой из функций
,
,
а также свойство производной функции
:
при дифференцировании вид функции не
меняется. Так как в системе уравнений
участие функций
,
согласовывается
при помощи коэффициентов
,
то, нетрудно догадаться, что решение
системы следует искать в виде:
,
, (2)
причем коэффициенты
,
=1,2
– будут определяться из условия, что
совокупность функций в записи (2) есть
решение системы уравнений (1):
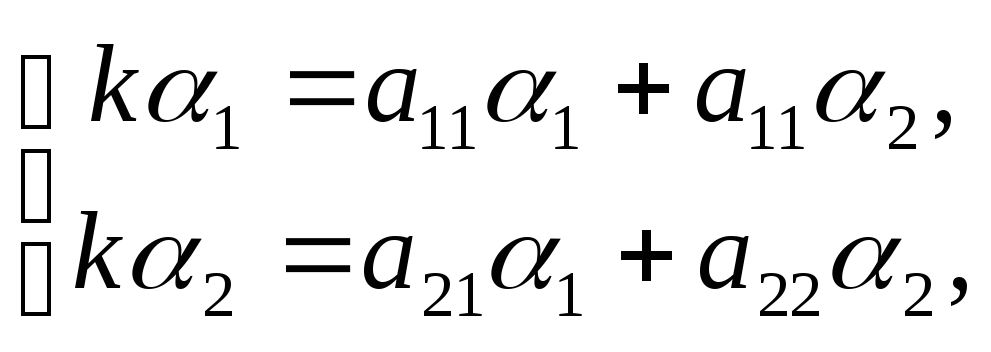или
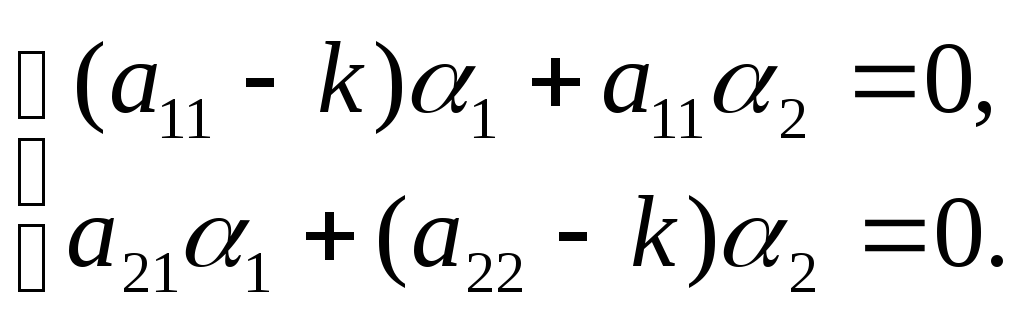(3)
Замечание:
система уравнений (3) записана с учётом
деления каждого из уравнений на общий
множитель:
.
Известно, система линейных однородных (алгебраических) уравнений имеет ненулевые решения только в случае, если её определитель равен нулю:
=
=0. (4)
Уравнение-многочлен
=0
называется характеристическим
для системы (1), его корни – характеристическими
корнями этой системы.
Дальнейшее использование полученных характеристических корней зависит от их вида. Различают случаи:
Случай-1.
Корни уравнения ∆(k)
= 0 действительные и различные:
,
.
Для каждого
из системы (3) определится набор
коэффициентов:
,
,
=1,2,
что определит полный набор решений
системы (1):
=
·
,
=
·
,
(5)
Учитывая теорему: сумма решений однородной системы уравнений – тоже решение, можем записать общее решение системы уравнений (1):
=
·
+
·
=
·
·
+
·
·
, (6)
где
,
- произвольные
постоянные. Запись (6) называют
общим
решением
системы уравнений (1).
Если заданы
начальные условия:
=
,
=
,
можно определить такие значения
,
,
что из множества интегральных кривых
будет выделена та, которая проходит
через точку
.
Случай-2.
Корни уравнения ∆(k)
= 0 комплексные:
=
.
Для пары корней
из системы (3) определятся:
=
i
;
=
i
.
Применим сначала знак
,
запишем решение системы (1):
=
·
=
·
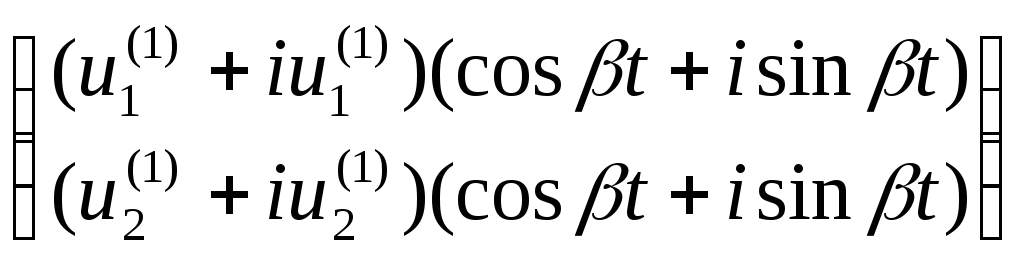, (7)
после выполнения операций умножения комплексных чисел и несложных тождественных преобразований в выражении (7) получим:
=
·
=
·
+
·
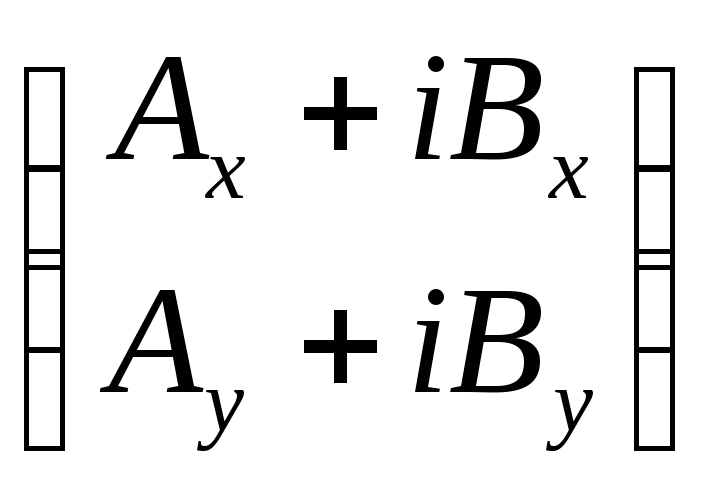. (8)
Аналогично, применяя
знак
,
получаем решение системы (1) с теми же
величинами, но только со знаком
перед мнимой единицей
:
=
·
=
·
–
·
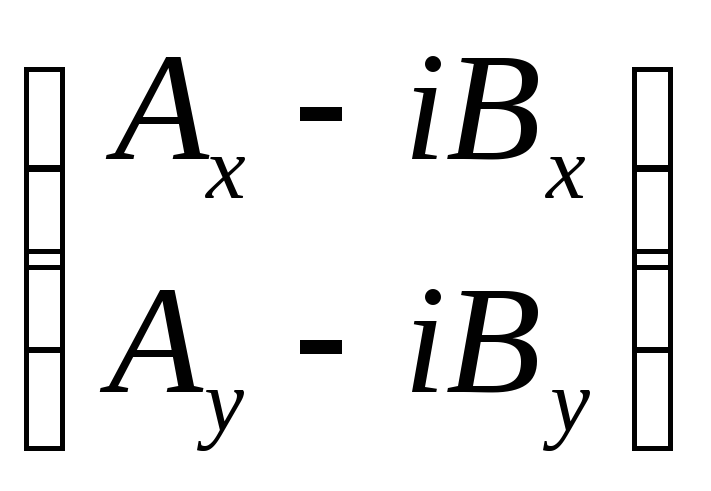. (9)
Известно (была доказана теорема!), что от записей решений системы (1) с использованием выражений (8) и (9) можно перейти к записям:
=
·
и 
=
·
. (10)
Учитывая теорему: сумма решений однородной системы уравнений – тоже решение, можем записать общее решение системы уравнений (1):
=
·
+
·
=
·
·
+
·
·
, (11)
где
,
- произвольные постоянные. Запись (11)
называют общим решением
системы уравнений (1) для пары
характеристических корней
.
Если заданы
начальные условия:
=
,
=
,
можно определить такие значения
,
,
что из множества интегральных кривых
будет выделена та, которая проходит
через точку
.
Случай-3.
Корни уравнения ∆(k)
= 0 действительные и равные:
=
=
.
Для каждого
из системы (3) определится набор
коэффициентов:
=
и
=
.
Это значит, что необходимо как-то учесть
равенство (кратность) характеристических
корней. В отличие от способа учёта
кратных корней при решении уравнений
высшего порядка для одной функции, в
случае системы уравнений ищут сразу
пару решений, используя
конструкцию:
=
·
,
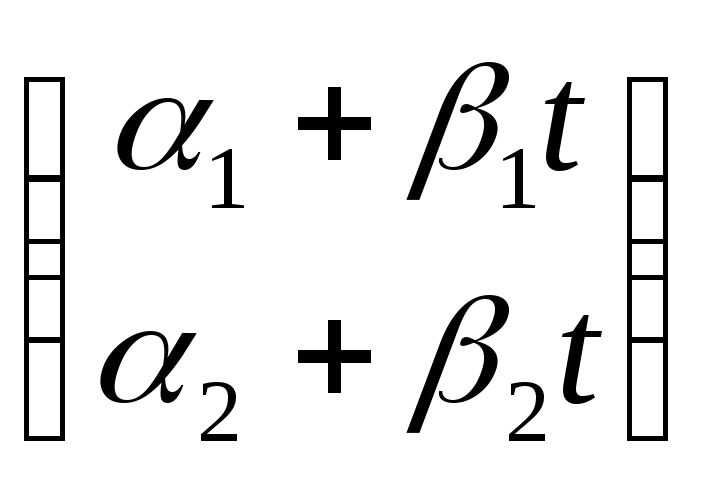(12)
Так как выражение
(12) должно быть решением, то необходимо
участвующие параметры подчинить
заданной системе уравнений (1). Подставим
(12) в систему (1), сократив на число
,
получим систему тождеств:
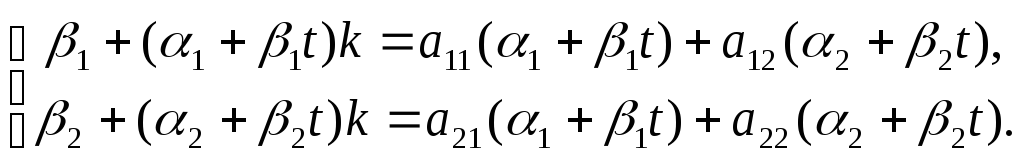(13)
Приравнивая в
тождествах (13) коэффициенты при одинаковых
степенях
,
получаем системы уравнений:
при
: 
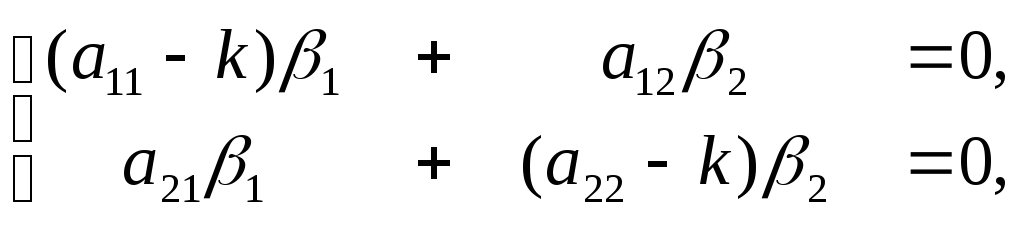(14)
при
: 
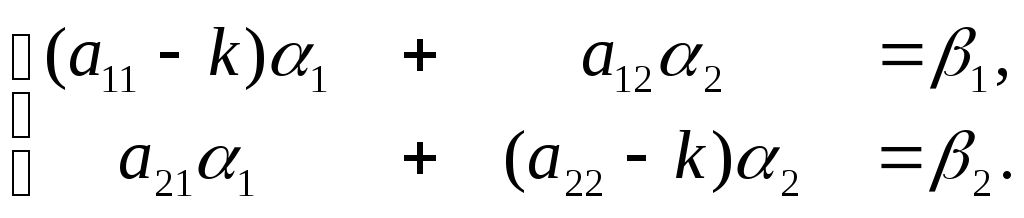(15)
Порядок нахождения
параметров
,
=1,2
из систем уравнений (14) и (15):
1). Из системы (14)
находим параметры
:
так как определитель системы равен 0,
то ненулевые решения у системы найдутся.
Принимая свободную неизвестную
=
,
получим в выражении (12) участие свободной
неизвестной. Параметр
будем использовать как произвольную
постоянную в записи решения системы
(1) – признак общего решения системы!
2). Используя
найденные параметры
,
решаем систему уравнений (15). Это система
также имеет ненулевые решения:
.
Принимая свободную неизвестную
=
,
получим в выражении (12) участие ещё одной
свободной неизвестной. Параметр
будем использовать как произвольную
постоянную в записи решения системы
(1) – признак общего решения системы!
Итак, получено общее решение системы дифференциальных уравнений (1) для случая кратных действительных корней.
Если заданы
начальные условия:
=
,
=
,
можно определить такие значения
,
,
что из множества интегральных кривых
будет выделена та, которая проходит
через точку
.
••• ≡ •••
Пример
1–432:
Решить систему уравнений:
при условии:
.
Решение:
1). Найдем
характеристические корни системы:
=
= 0, откуда получаем:
=2,
=4.
Для каждого
определится набор коэффициентов:
,
,
что определит полный набор решений
системы (1):
=
∙
=
∙
,
=
∙
=
∙
, (1)
2). Для определения
векторов
,
составим систему уравнений:
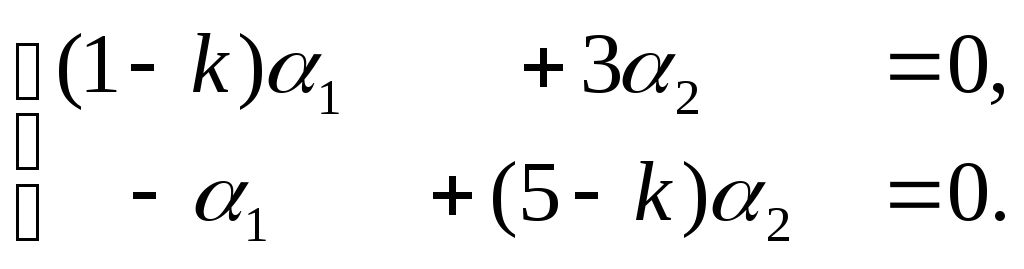(2)
3).
Для
корня
система (2) имеет решение
=
;
для корня
система (2) имеет решение:
=
.
4). С учетом полученных
векторов
,
составим общее решение исходной системы
дифференциальных уравнений:
=
+
=
∙e2t
+
∙e4t.
(3)
5). Учитывая начальные условия и запись общего решения, получим:
=
+
,
откуда
=1,
=0. (4)
6). Используя
результаты (4), запишем частное решение
системы, удовлетворяющее начальным
условиям: 
=
∙e2t. (5)
Ответ:
Общее решение системы:
=
∙
+
∙
,
частное:
=
∙
.
Пример
2–434:
Решить систему уравнений:
Решение:
1). Найдем
характеристические корни системы:
=
= 0, откуда получаем:
.
Для каждого
определится набор коэффициентов:
,
,
что определит полный набор решений
системы (1):
=
∙
=
∙
,
=
∙
=
∙
. (1)
2). Для определения
векторов
,
составим систему уравнений:
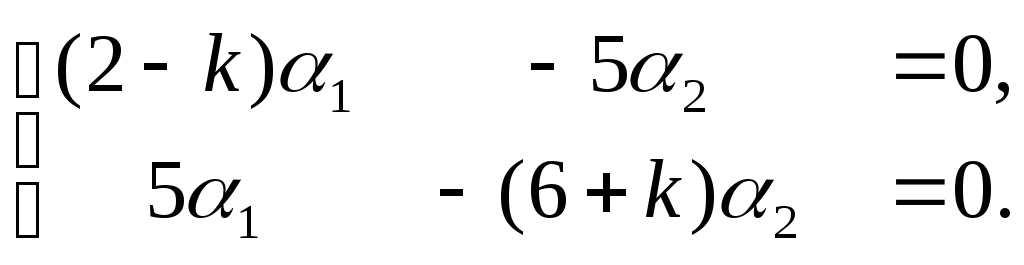(2)
3). Для корня
система (2) имеет решение:
=
,
для которого можно записать: 
=
∙
=
∙
.
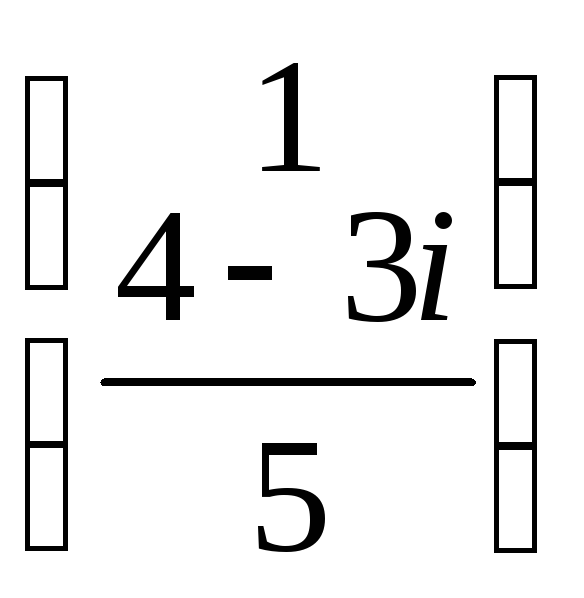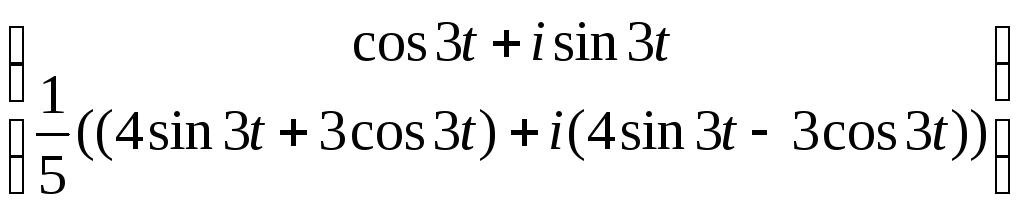4). Для корня
система (2) имеет решение:
=
,
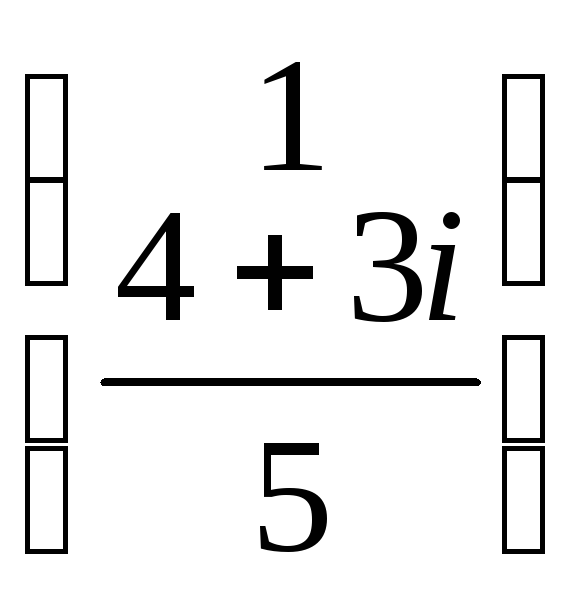для которого можно записать: 
=
∙
=
∙
.
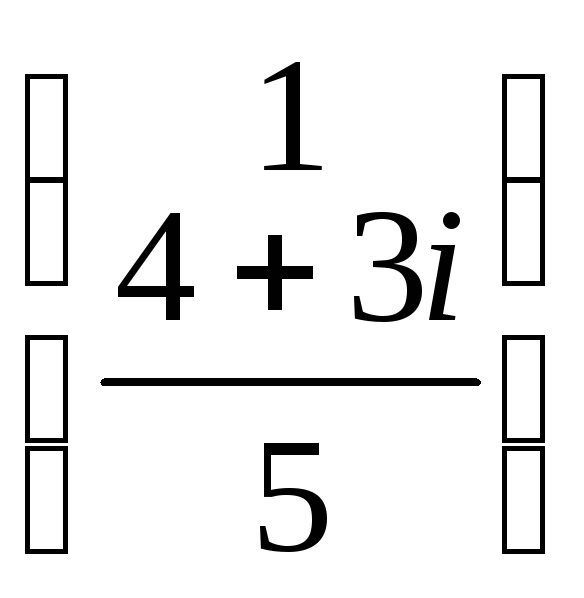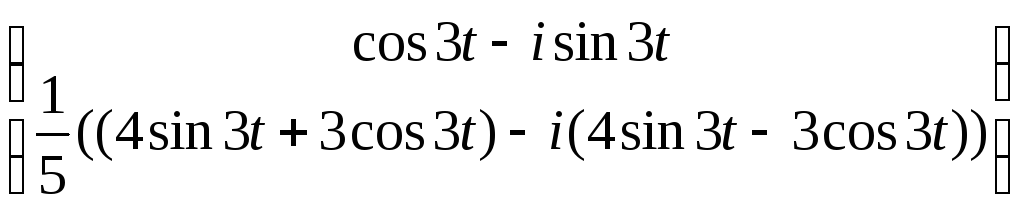5). Видим: решения
и
комплексно-сопряженные. Это значит
(Теорема!), что в качестве частных решений
системы уравнений можем взять отдельно
мнимую и действительную части. Получаем:
=
∙
,
=
∙
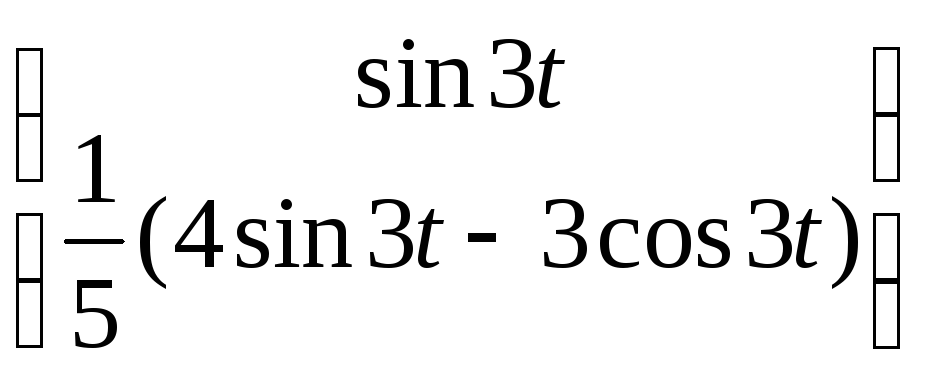, (3)
6). С учетом полученных частных решений (3) составим общее решение исходной системы дифференциальных уравнений:
=
+
=
∙
+
∙
.
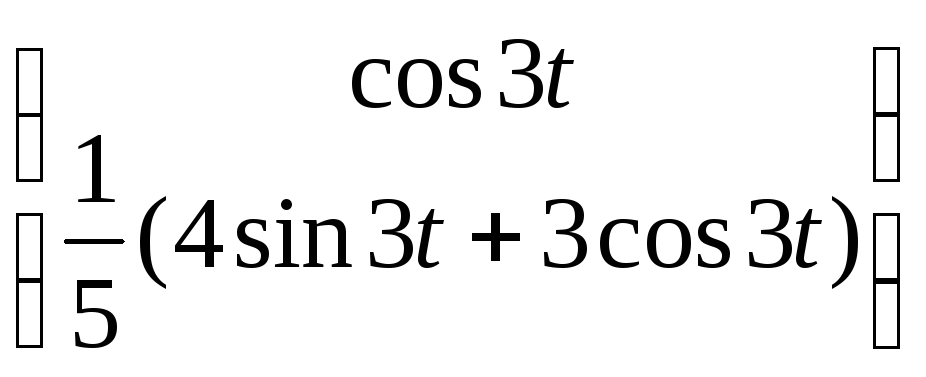(4)
Ответ:
Общее решение:
=
∙
+
∙
.
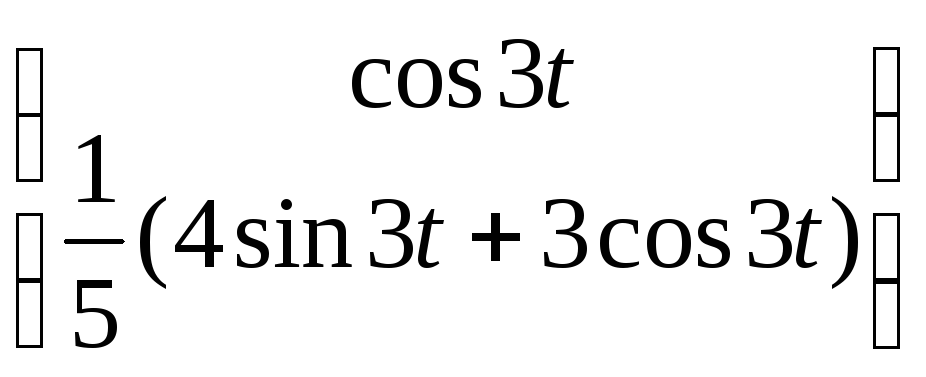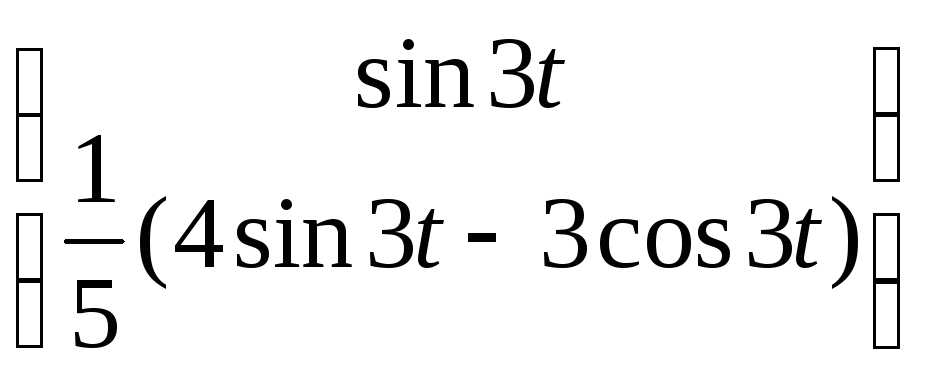Пример
3–436:
Решить систему уравнений:
при условии:
.
Решение:
1). Найдем
характеристические корни системы:
=
= 0, откуда получаем:
=
=–3.
В этом случае решение системы ищут в
виде:
=
,
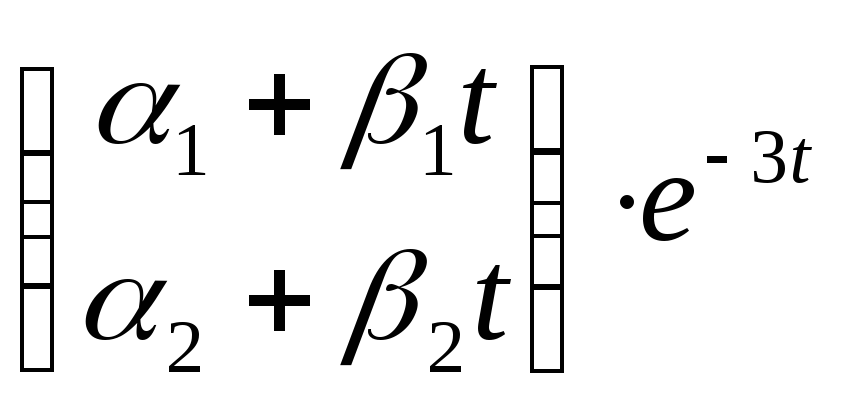(1.3)
2). Подставим (1.3) исходную систему уравнений:
(2.3)
3). Так как в системе
уравнений (2.3) каждое уравнение является
тождеством, то все неизвестные коэффициенты
найдем, приравнивая коэффициенты при
одинаковых степенях:
и
:
при
: 
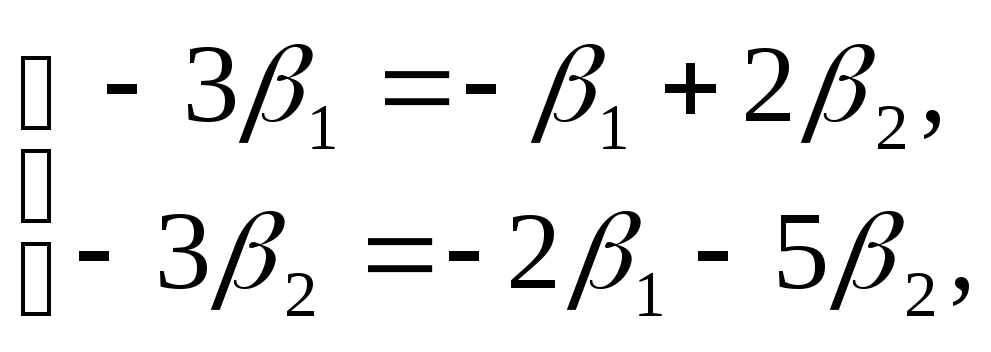откуда получаем:
; (3.3)
при
: 
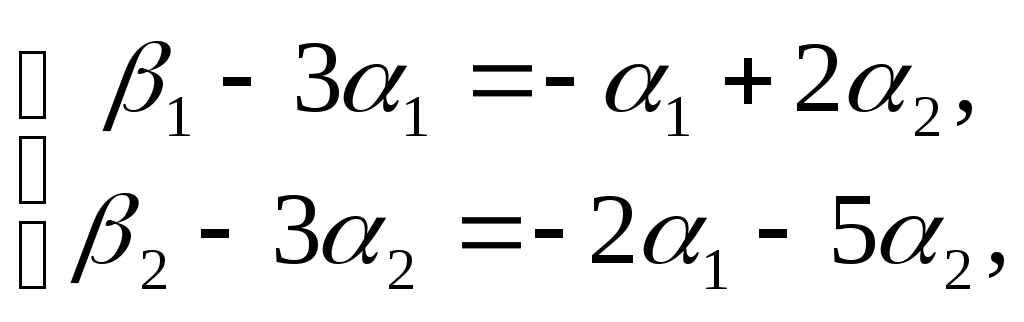откуда получаем:
; (4.3)
из (3.3) примем:
,
,
из (4.3): примем
,
.
Замечание: решение системы (3.3), (4.3) проводится по известным правилам из курса «Линейная алгебра»: объявление неизвестных «свободными» содержит некоторые импровизации, которые не влияют на выражение частного решения при заданных начальных условиях!
4). Учитывая
полученные значения коэффициентов,
можно записать общее решение заданной
системы: 
=
∙
.
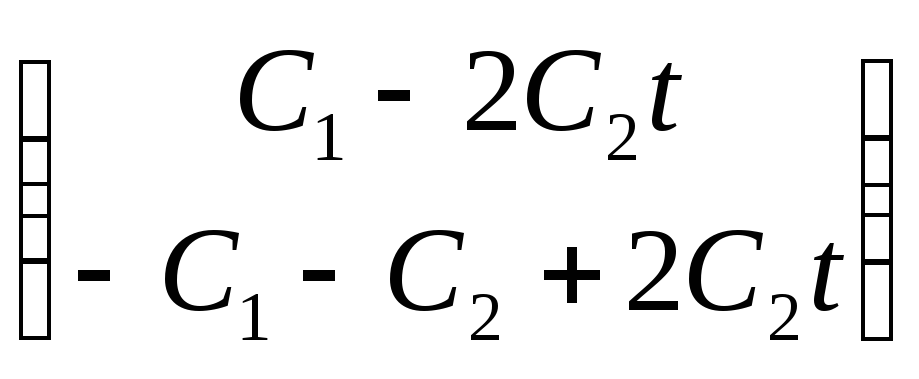(5.3)
5). Учитывая начальные условия и запись общего решения, получим:
=
,
откуда
и
=
∙
. (6.3)
Ответ:
Общее решение системы:
=
∙
,
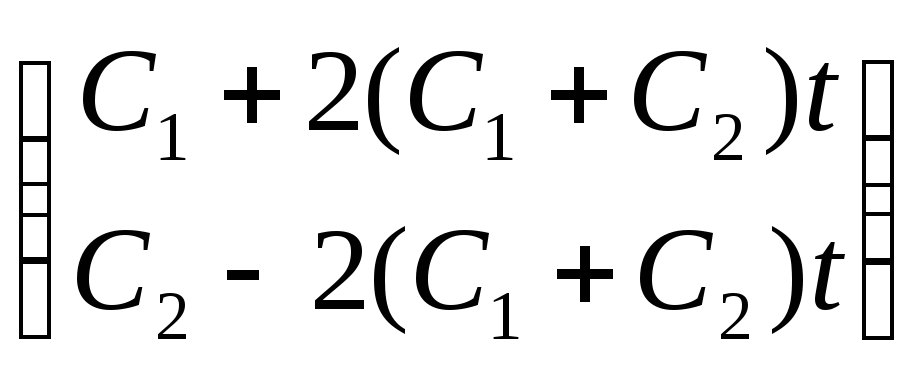частное:
=
∙
.
Пример
4–438:
Найти частное решение системы:
если:
.
Решение:
1). Найдем
характеристические корни системы:
=
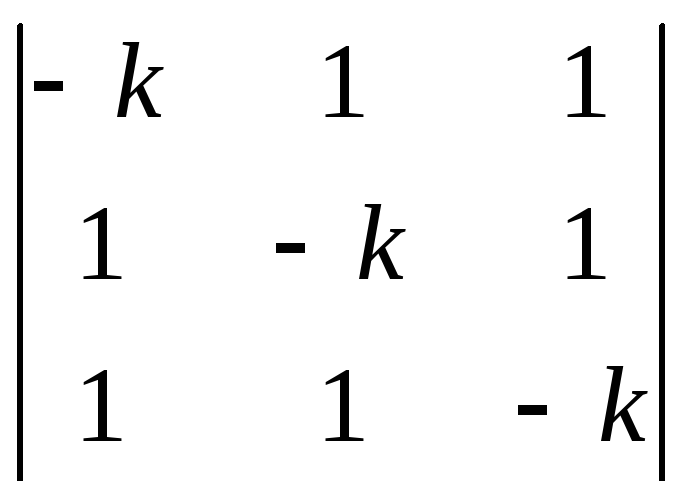= 0, откуда получаем:
=
=–1;
=2.
В этом случае решение системы для
кратного корня
=–1
необходимо искать в виде: 
, (1.4)
2). Подставим (1) исходную систему уравнений:
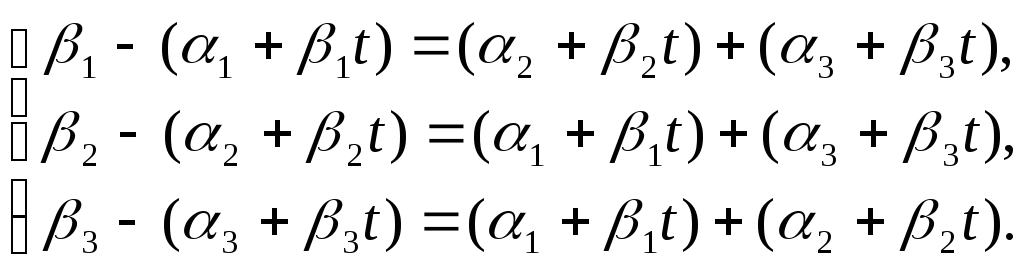(2.4)
3). Так как в системе
уравнений (2.4) каждое уравнение является
тождеством, то все неизвестные коэффициенты
найдем, приравнивая коэффициенты при
одинаковых степенях:
и
:
при
: 
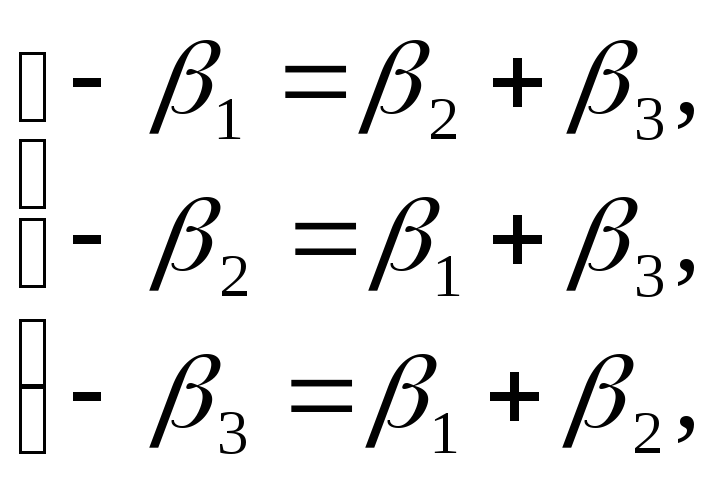откуда получаем:
; (3.4)
при
: 
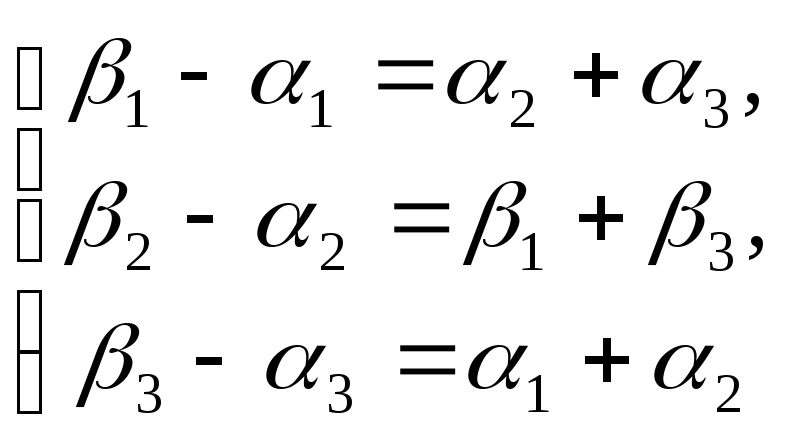получаем:
=
. (4.4)
В данной задаче,
если в уравнении (3.4) принять в качестве
свободных неизвестных две из неизвестных
,
то из (4.4) получается
,
то есть неизвестные не могут быть
свободными в общей системе (3.4),(4.4). Тогда
из (4.4):
получаем значения остальных параметров:
,
,
.
4). Учитывая
полученные в (3) значения коэффициентов,
можно представить запись (1) в виде: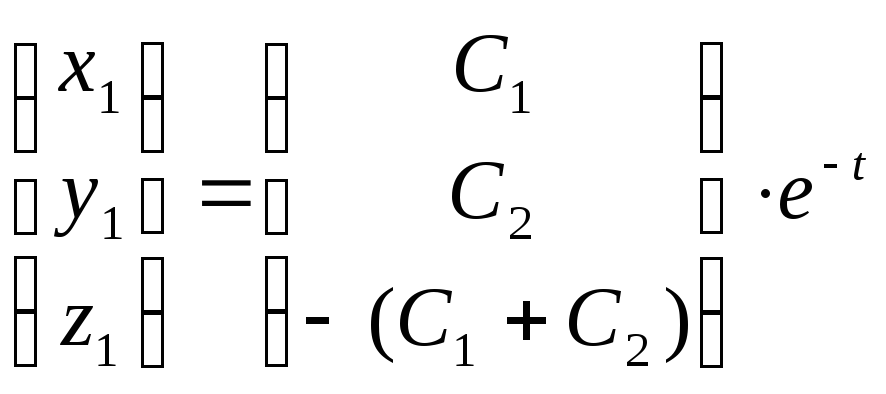 
,
(5.4)
5). Для определения
вектора
составим систему уравнений:
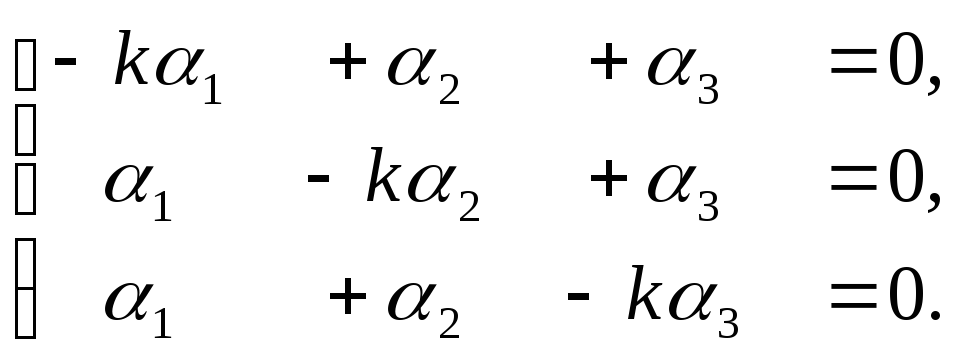(6.4)
6). Для корня
из системы (5) имеем:
=
,
тогда:
=
∙
∙
. (7.4)
7). С учетом полученных решений (4.6) и (6.6), составим общее решение исходной системы дифференциальных уравнений (с учетом свойств матриц):
=
+
∙
∙
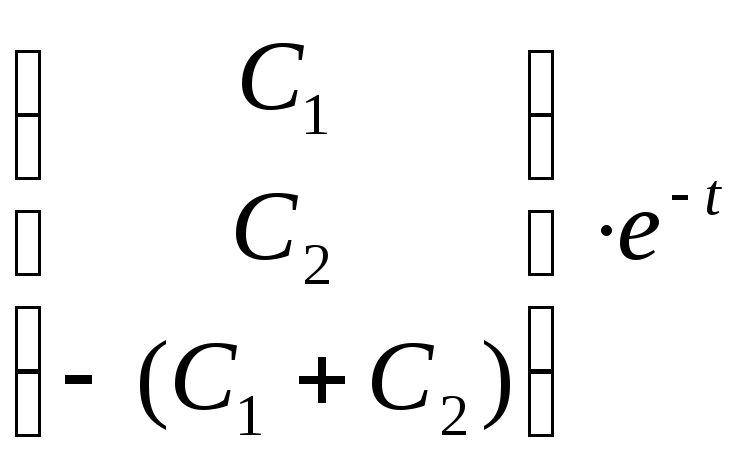. (8.4)
8). Учитывая начальные условия и запись общего решения, получим:
=
+
∙
,
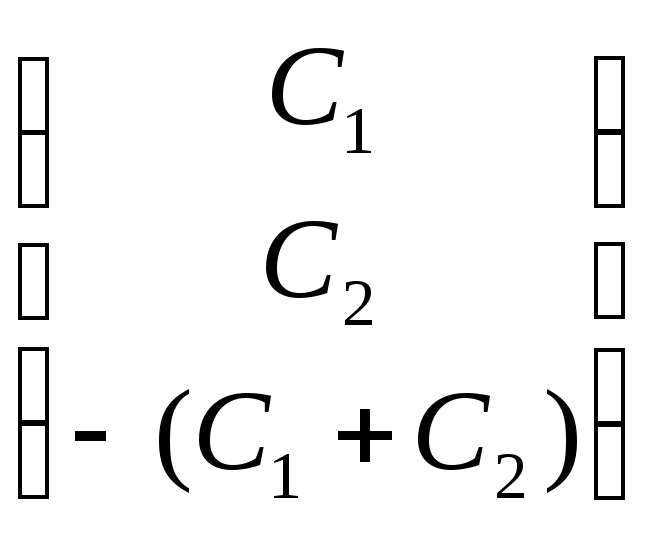откуда
=1,
=1,
=1. (9.4)
9). Используя
результаты (8.6), запишем частное решение
системы, удовлетворяющее начальным
условиям: 
=
∙
+
∙
. (10.4)
Ответ: частное
решение системы:
=
∙
+
∙
.
Пример
5–440:
Решить систему уравнений:
Решение:
1). Найдем
характеристические корни системы:
=
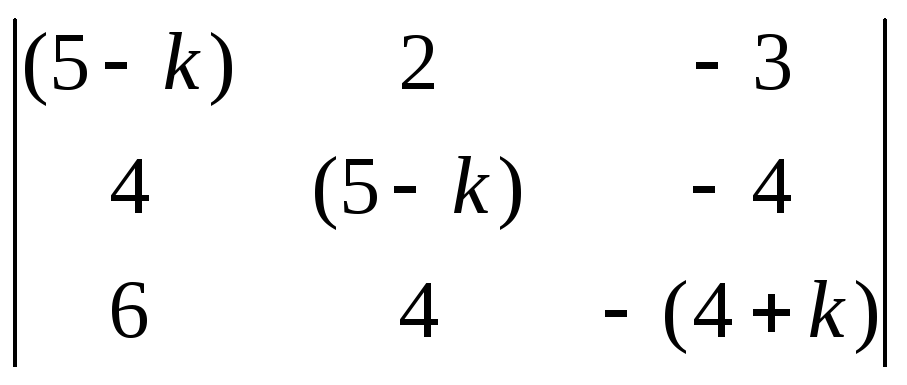= 0, откуда получаем:
=1,
=2;
=3.
Замечание:
решение уравнения
=
=0
проводится по Виету: угадали все корни
как множители числа 6.
2). Для каждого
определится набор коэффициентов:
,
,
,
что определит полный набор решений
системы (1):
=
∙
=
∙
,
=
∙
=
∙
, 
=
∙
=
∙
,
(1.5)
3). Для определения
векторов
,
,
составим систему уравнений:
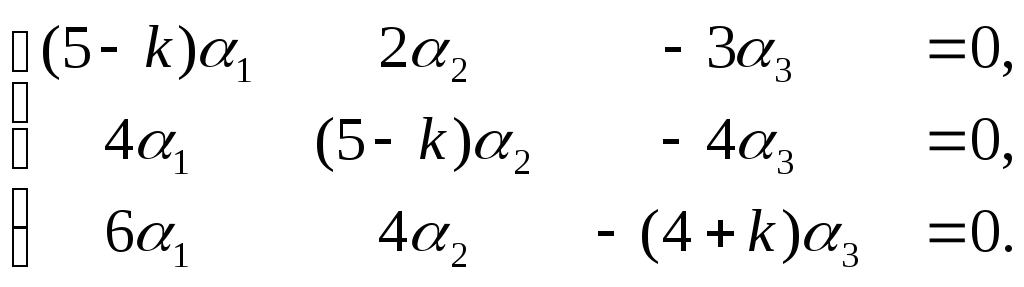(2.5)
4).
Для
значения
система (2.5) имеет решение:
=
;
для значения
система (2.5) имеет решение:
=
;
для
система (2.5) имеет решение:
=
.
5). С учетом полученных
векторов
,
,
составим общее решение исходной системы
дифференциальных уравнений:
=
+
+
=
∙
+
∙
+
∙
.
(3.5)
Ответ:
Общее решение системы:
=
∙
+
∙
+
∙
.
☻
Вопросы для самопроверки:
-
Как по записи системы уравнений 1-го порядка определить, что она линейная?
-
Почему линейная система однородных уравнений с постоянными коэффициентами удовлетворяет требованиям теоремы «о существовании и единственности решений»?
-
Как записывают характеристический многочлен для системы линейных однородных уравнений с постоянными коэффициентами?
-
Как записывают общее решение системы линейных однородных уравнений с постоянными коэффициентами?
-
Как находят частное решение системы линейных однородных уравнений с постоянными коэффициентами?
-
Как учитывают кратность характеристических корней при решении системы линейных однородных уравнений с постоянными коэффициентами?
Задачи для самоподготовки:
Пример
C15–1: Решить
систему линейных уравнений:
Ответ:
общее решение
системы:
=
+
=
∙
+
∙
.
Пример
C15–2: Найти
частное решение системы:
для условий:
.
Ответ:
общее решение
системы:
=
∙
+
∙
.
частное
решение: 
=
∙e5t.
Пример
C15–3: Решить
систему линейных уравнений:
Ответ:
общее решение:
=
∙
.
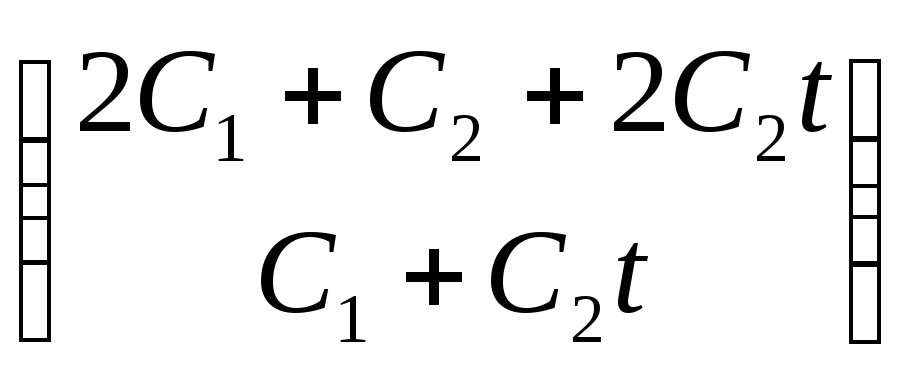Пример
C15–4: Найти
частное решение системы:
для условий:
.
Ответ:
частное решение,
удовлетворяющее начальным условиям:
.
Пример
C15–5:
Решить систему линейных
уравнений:
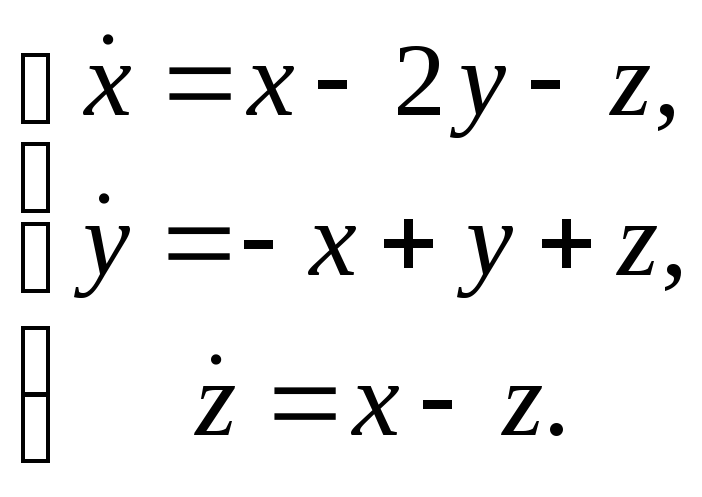
Ответ:
Общее решение
системы:
=
∙
+
+
∙
.
•• ☻☻ ••