3. Содержание лабораторной работы

1. Решить дифференциальное уравнение, соответствующее данному звену.

2. Построить переходную функцию звена.

3. Построить частотную характеристику звена.

4. Пример выполнения лабораторной работы

Пусть дано колебательное звено с параметрами к=2,T=1.5 и =0.7.

1. Решение дифференциального уравнения, соответствующего данному звену.

Дифференциальное уравнение колебательного звена имеет вид:

(Т2р2+2Тр+l)X2(t)=kXl(t) .

Принимая x1(t)= [1 + sign(t)] /2 решаем уравнение относительноx”(t)

и сделав подстановку y2 =x2’ , y1=x2 ,получим систему обыкновенных дифференциальных уравнений:

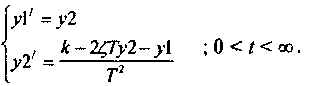
Решение у2 и есть искомая переходная функция звена.

Получим выражения для построения частотной характеристики:

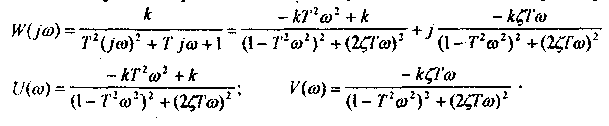
2. Построение графика зависимости выходной функции звена от входной

Создаем файл описания полученной системы уравнений MYFUN.M:

function yprime = myfun(t,y);

k=-2;

Т=1.5;

z=0.7;

yprime = [y(2); (k-2 . * z. * Т. * у (2) - y(1))./T./T];

Во второй строке видно задание правых частей системы дифференциальных уравнений. Создадим файл LAB1 .М:

t0-= 0;

tfinl = 15;

y0=[0 0] '

tol= 1.e-3;

trace = 1;

k=2;

T=1,5;

z=0.7;

[t,v] =ode23('mvfun'.t0.tfinal,y0,tol,trace);

plot(t,y(.;1));

title('Time history');

xlabel(‘time');

pause

Теперь, запустив MATLAB, вводим lab1 и получаем график выходной

функции звена (рис. 4.1)

3. Построение частотной характеристики звена

Дописав в конец файла LAB 1 .М следующий текст MATLAB построит два заданных графика (рис. 4.1 и рис. 4 2)

for 1=1:70,

w=(i-l)./20;

znam=(1-T^2.*w.^ 2).^ 2+(2.*z *T *w)^2;

u(i)=(k-k.*T^2.*w.^2)./znam;

v(i)=((-k).*z.*T.*w)./znam;

end;

plot(u,v);

xlabel('U(w)');

ylabel('V(w)');

На данном годографе передаточной функции U(0)=2 V(0)=0

U(+)=0, V(+)=0 '~

5. Рекомендации по выполнению лабораторной работы

Некоторые типы звеньев нельзя описать в MATLAB, т. к. их решением является 8-функция (рис. 5.2). Идеальное дифференцирующее звено - пример такого звена. Его решение 5-функция такая, что

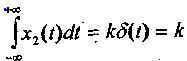
Другое подобное звено - идеальное звено с введением производной. Его

pешение (рис. 5.3) есть функция Хевисайда (рис. 5.1) плюс-функция.

Для описания инерциального дифференцирующего звена можно вместо - функции (эквивалентной в данном случае X1 ‘) подставить функцию

Достаточная степень точности

обеспечится импульсом длительностью t=0.2 единицы времени и амплитудой А =5 единиц.

Приложение Варианты заданий к лабораторной работе.

	ВАРИАНТЫ
	I	2	3	4	5	6	7	8	9	10	11	12	13
k	2	0.5	1	3	2	3	1	5	4	3	2	4	1
Т	0.5	2	4	1	1	0.8	1.2	1.6	0.6	1	0.7	1.2	0.9
					10	5	3	6	6	0.1	0.5	0.3	0.2
	Апериодическое				Апериодическое 2 порядка					Колебательное

	В А РИА Н Т Ы
		14 -15	16	17	18	19	20	21	22	23	24	25	26
k	1	0.5	10	3	2	3	3	1	4	2	5	11	6.5
Т					1	3	0.5	5	3.5	5	10	10	8
	Идеальное интегрирующее				Инерциальное интегрирующее					Инерциальное дифференцирующ