Весовая функция звена.

Весовой функцией звена называется оригинал (т.е. обратное преобразование Лапласа) передаточной функции

где s, - все полюса передаточной функции W(s). В этой формуле Res обозначает вычеты (см. теорию функций комплексного переменного).

Поскольку при нулевых начальных условиях

X2(s)=W(s)X2(s), то будет иметь место равенство

в том случае, если Х1= 1, т.е. если .

Следовательно, физический смысл весовой функции звена k(t) есть реакция звена на единичный импульс, длительность которого стремится к нулю, а амплитуда к бесконечности, причем их произведение равно 1.

Иначе говоря, весовая функция представляет переходный процесс на выходе звена при подаче на его вход единичного импульса.

Зная весовую функцию звена k(t), можно определить его передаточную функцию:

W(s)=L{k(t)}.

Переходная функция звена.

Переходной функцией h(t) называется реакция звена на единичное ступенчатое воздействие, т.е. переходный процесс на выходе Х2 при единичном скачке 1(t) на входе звена x1.

Следовательно,

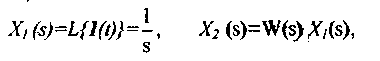
откуда

Поскольку известно, что (имея в виду обобщенные функции)

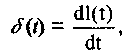
то имеем следующее соотношение между весовой и переходной функциями

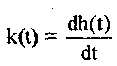
1. Типы звеньев систем автоматического управления и их характеристики

Типы звеньев систем автоматического управления и регулирования различаются по виду их передаточной функции (или дифференциального уравнения), определяющей все их динамические свойства и характеристики.

Основные типы звеньев делятся на три группы: позиционные, дифференцирующие и интегрирующие.

Позиционными звеньями называются такие, в передаточной функции которых

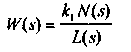
многочлены N(s) и L(s) имеют свободные члены (равные 1), т.е. эти звенья обладают статической характеристикой x2=k1x1 (при s=0), определяющей их состояние равновесия (свойство позиционности).

У дифференцирующих звеньев в выражении (1.1) отсутствует свободный член числителя, т.е. для однократно дифференцирующего звена будет

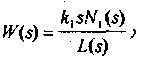
свободный член, равный 1. Для двукратно дифференцирующего звена

Передаточные функции интегрирующих звеньев имеют соответственно вид

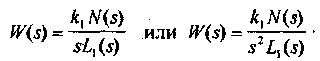где L1(s) имеет свободный член, равный 1.

1.1 Позиционные звенья и их характеристики

Апериодическое (инерционное) звено. Уравнение и передаточная функция звена:

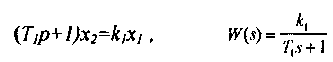
Амплитудно-фазовая частотная характеристика звена:

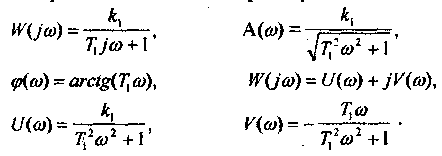
Логарифмическая амплитудная частотная характеристика имеет вид

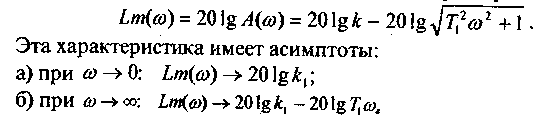
Чем меньше постоянная времени звена T1, тем больший диапазон частот входного сигнала "пропускает" звено с усилением, т. к.

Переходная функция, согласно решению уравнения звена, при x1=1(t) и нулевых начальных условиях имеет вид

а весоая функция

Величина T1 характеризует степень инерционности звена, т.е. длительности переходного процесса.

Примером апериодического звена является (в первом приближении) электродвигатель, если x1 - управляющее напряжение, x2 - угловая скорость вала. Другой пример - цепочка LR

(рис. 1.1).