Министерство общего и профессионального образования российской федерации

Московский государственный институт электроники и математики (Технический университет)

Кафедра "Вычислительные системы и сети"

Изучение типовых звеньев систем управления

Методические указания к лабораторной работе по дисциплине Основы теории управления

Москва 1998

Предисловие

В данном руководстве изложены основные теоретические знания, необходимые для лабораторной работы, и пример ее выполнения с использованием пакета MATLAB.

Цель лабораторной работы - изучение с помощью ПВМ переходных и частотных характеристик типовых звеньев систем управления.

Теоретическое введение

Чтобы составить уравнения динамики системы автоматического управления или регулирования, система разбивается на звенья. Затем рассматривается каждое звено системы в отдельности: Входная x1 и выходная х3 величины соответствуют физическим величинам, выражающим воздействие предыдущего звена на данное звено (x1) и воздействие данного звена на последующее (x2).

Звено системы может являться техническим устройством любой физической природы, конструкции и назначения. Поэтому составление уравнения динамики каждого конкретного звена системы является предметом соответствующей конкретной области технических наук (электротехники, теплотехники, динамики полета и т.п.), к которым и следует каждый раз обращаться.

Допустим, что в результате составления уравнения динамики какого-нибудь конкретного звена получилось следующее линейное дифференциальное уравнение второго порядка:

В теории автоматического регулирования принято приводить

уравнение звена к стандартному виду в символической записи

, (*)

где р обозначает операцию дифференцирования p=. Здесь введены постоянные времени, которые в данном случае будут

и коэффициент усиления (передаточное число) звена

Очевидны следующие размерности этих постоянных:

Т1 [сек], [сек],[сек],

В установившемся состоянии, когда X1=const и X2=const получаем из (*) уравнение статики данного звена

X2=k1X1

коэффициент усиления k, определяет крутизну наклона соответствующей линейной статической характеристики звена (k1=tg а, где а - угол наклона характеристики к оси Ох1).

Передаточная функция звена.

Ее определение дается на базе преобразования Лапласа:

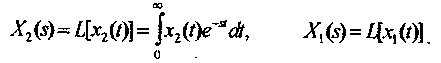
Пусть даны начальные условия:

Тогда: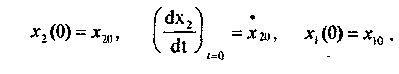

Применив это преобразование к дифференциальному уравнению звена

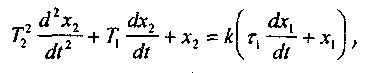
получим:

(**)

где через B(s) обозначим многочлен, включающий в. себя все члены с величинами начальных условий.

Передаточной функцией звена W(s) называется отношение изображения Лапласа выходной величины к входной:

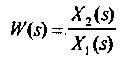
при нулевых начальных условиях (B(s)=0 ). В данном случае согласно (**) имеем

(***)

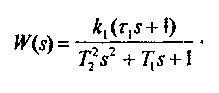Сравнивая полученное выражение с дифференциальным уравнением звена(***), видим, что формально передаточную функцию звена можно составлять как отношение операторных многочленов правой и левой частей уравнения звена. И наоборот, зная передаточную функцию (***), легко написать его уравнение, имея в виду что числитель передаточной

функции соответствует правой части уравнения(*), а знаменатель передаточной функции (***) - левой части уравнения (*).

В общем случае передаточная функция звена имеет вид

где N(s) и L(s) - многочлены с коэффициентами 1 в младших членах, причем степень N(s), как правило, ниже степени L(s).