Апериодическое звено второго порядка.

Уравнение и передаточная функция звена имеют вид

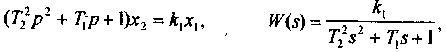
причем предполагается, что T1>=2T2 так как при этом корни характеристического уравнения

будут вещественными. Передаточную функцию апериодического звена второго порядка можно записать в виде

где

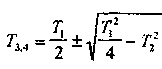
Амплитудно-фазовая частотная характеристика звена:

Логарифмическая амплитудная частотная характеристика звена:

При (T1<2T2) звено переходит в колебательное (см. ниже) состояние, поэтому постоянная Т1, определяющая инерционность звена, является в то же время демпфирующим фактором (увеличение Т1 приводит к отсутствию колебаний). Переходная и весовая функции аналогично предыдущему имеют вид

Примерами такого звена являются: а) двигатель постоянного тока при учете инерционности цепи якоря; б) электро машинный усилитель; в) двойная цепочка LR.

Колебательное звено.

Уравнение и передаточная функция звена:

причем предполагается T1<2T2, так что корни характеристического уравнения - комплексные. Общепринята запись передаточной функции колебательного звена в виде

где Т=Тг, =T1/(2T2), причем 0<< 1 , так как при= > 1 звено становится апериодическим второго порядка.

Амплитудно-фазовая частотная характеристика звена:

Амплитудная характеристика уменьшается с увеличением , т.е. A() < k1 , если 1>>0.707. При<0.707 появляется "горб" на характеристике A(), который уходит в бесконечность при)0. Поэтому величина,=T1/(2T2) называется параметром затухания. Отсюда видна роль

постоянных времени T1 и Т2 в уравнении звена: постоянная T1 "раскачивает" колебания, а T2 - "демпфирует" их.

Логарифмическая амплитудная частотная характеристика звена

Переходная и весовая функции колебательного звена соответственно имеют вид

При колебания становятся незатухающими, а приколебания вырождаются в апериодический процесс.

Пример колебательного звена - на рис. 1.2 .

Частный случай колебательного звена, при =0 , когда h(t) и k(t) становятся незатухающими (периодическими), носит название консервативного звена.

1.2 Интегрирующие и дифференцирующие звенья и их характеристики

Основные данные об интегрирующих и дифференцирующих звеньях приведены в таблице 1.

Таблица 1

2. Описание пакета matlab V. 3.5g

Пакет MATLAB* состоит из исполняемого файла PCMATLAB.EXE и набора файлов с расширением «.М». В М-файле содержится описание функции или процесса вычисления на языке MATLAB'a. Удобно все вычисления оформить в виде такого файла, тогда, войдя в среду MATLAB достаточно будет набрать имя этого файла и все вычисления будут производиться автоматически. Также можно выполнять все вычисления в командном режиме. Переменные, используемые при таком способе вычислений сохраняются в рабочей области MATLAB'a и доступны во всех последующих операторах. Здесь будет описан первый способ организации вычислений, для этого надо будет создать собственный М-файл. В этом файле можно использовать стандартную функцию MATLAB'a -ODE23, которая описана в файле ODE23.M и предназначена

для интегрирования обыкновенных дифференциальных уравнений. Пример использования этой функции приводится в файле ODEDEMO.M .

Для написания программы вычислений потребуются некоторые конструкции языка, используемого в MATLAB'e.

11 - квадратные скобки используются для формирования векторов и матриц. Так [6.9 9.64 SQRT(-1)] обозначает вектор с тремя элементами. Вместо пробела в качестве разделителя можно использовать запятые. [1+X, 2-1 3] не тоже самое что [1 +Х 2 -1 З]. В первом случае три элемента, а во втором пять. Точка с запятой служит для разделения строк матрицы. [1011 12; 13 14 15] это матрица с двумя строками и тремя столбцами.

( ) - круглые скобки используются для изменения приоритета вычислений в арифметических выражениях, для обозначения списка аргументов функции, для выделения элементов векторов и матриц. Если V и Х - векторы, то X(V) это [X(V(1)), X(V(2)), ... , X(V(N))]. Элементы вектора V округляются до ближайшего целого. Возникает ошибка, если какой-либо индекс меньше 1 или больше размерности X.

. - точка используется как десятичная точка и как показатель поэлементной операции. Например, С=А ./ В это матрица с элементами c(ij)=a(ij)/b(ij).

, - запятая разделяет элементы матрицы и аргументы функции. Также используется для разделения операторов в многооператорных выражениях. В этом случае может использоваться и точка с запятой для подавления печати.

; - точка с запятой внутри квадратных скобок означает конец строки матрицы. После выражений и операторов для их разделения и подавления печати.

% - знак процента в строке означает, что все символы после него будут проигнорированы MTLAB'ом. Т. о. процент используется для комментариев.

: - двоеточие используется в описании цикла и по возможности для других целей, например, J:K тоже, что и [J, J+1, ... , К]. Если J>K, то J:K эквивалентно [ ]. J:S:K означает то|же, что и [J, J+S, J+2S, ... , К ]. Двоеточие также может быть использовано для выделения строк, колонок и элементов матриц и векторов. А( : ) это все элементы матрицы А, представляемые в виде одной колонки. А(: , J) это J- я колонка A. A(J:K) интерпретируется как A(J), A(J+1), ... , А(К). А( : , J:K) это А( : , J), А( : , J+1),...,A(:,K). .

' - апостроф транспонирует матрицу. Если Х - вектор-строка, то X' -вектор-столбец. Апострофы также ограничивают ASCII строку.

+ - плюс. X+Y складывает матрицы. Х и Y должны иметь одинаковые размерности. Скалярные величины могут быть прибавлены к любому другому объекту.

- - минус. X-Y вычитает матрицы. Х и Y должны иметь одинаковые размерности. Скалярные величины могут быть вычтены из любого другого объекта.

- - умножение. Х * Y дает матрицу равную матричному произведению Х на Y. Количество колонок в матрице Х должно быть равно количеству строк в матрице Y. Поэлементное умножение описывается выражением Х .* Y . Х и Y в этом случае должны иметь одинаковые размерности. Скалярная величина (матрица 1 на 1) может умножаться с любым объектом.

^- степень. Z=X^y это Х в степени у, где у -скаляр. Степень вычисляется последовательностью умножений. Z=X^Y, где Х и Y -матрицы приводит к\ошибке. Z=X.^Y выполняет поэлементное возведение в степень. Х и Y должны иметь равные размерности, если только один из них не скаляр.

= - знак равенства выполняет операцию присваивания == - логическая операция эквивалентности

~ - логическое НЕ

~= - неравенство

& - логическое И

| - логическое ИЛИ

- сравнение (больше)

< -сравнение (меньше)

CLEAR - очищает все переменные из рабочей области MATLAB'a. CLEAR X удаляет только переменную иди функцию X. CLEAR FUNTIONS удаляет из рабочей • области все откомпилированные М-функции.

ECHO - ECHO ON включает режим отображения содержимого М-файлов. ECHO OFF соответственно выключает этог режим. ECHO ON ALL переключает все команды ECHO во всех исгользуемых файлах в режим ON.

END - обозначает конец описания ближайшего FOR, WHILE или IF оператора.

EXIT - выход из среды MATLAB. Оператор QUIT и CTRL-Z делают TdjsKe самое.

ЕХР - ЕХР(Х) вычисляет экспоненту каждого элемента матрицы (вектора,скаляра).

FOBS - организует цикл. Синтаксис:

FOR <переменная> = <выражение>, <оператор>, ... ,<оператор> END

Переменной по очереди присваиваются элементы выражения и выполняются операторы. Выражение обычно описывается в форме X:Y. Например:

FOR К= 1:99,

FORJ=K:100, A(K,J)=1;

END

END

FUNCION - добавляет новую функцию к MATLAB'у. Функция •описывается в терминах других, уже описанных функций в отдельном М-файле, имя которого совпадает с именем функции. В первой строке данного файла должна быть строка, описывающая функцию. Например, в файле STAT.M содержится следующий текст:

Function [mean, stdev] = stat ( x) n = prod (size(x));

mean = sum(x) ./n;

stdev = sqrt(sum(x^2) / n – mean^2)•, Тогда если в каком-либо другом файле написать, например, [т, x]=STAT(Y), то т и х примут значения, присвоенные mean и stdev соответственно. Все переменные, используемые для определения функции являются локальными по отношению к ней.

IF - выполнение операторов по условию. Простейшая форма:

IF <переменная>, <операторы> END

Операторы выполняются только тогда, когда все элементы переменной не нулевые. Пример:

IF I = = J,

A(i,j)=2;

ELSEIF ABS(I-J)== 1, A(i,j)=-l;

ELSE

A(i,j)=0;

* END

LOAD - считывание с диска переменных и их значений, записанных с помощью SAVE. LOAD data.mat - считывает данные из файла data.mat.

PAUSE - приостанавливает выполнение программы до нажатия пользователем какой-либо клавиши. PAUSE (n) - пауза на п секунд.

PLOT - построение графиков. PLOT(X,Y) - ставит точки с координатами

(X(i), Y(i)) для всех i (X и Y - векторы). Если Х или Y - матрицы, то вектор откладывается по одной оси, а колонка или строка матрицы по другой, т. о. получаем несколько графиков. Множество графиков можно также получить написав PLOT(X1,Y1,':',X2,Y2,'+'). Здесь один график будет вычерчен точечной линией, а другой помечен крестиками.

SAVE - сохраняет в файле переменные рабочей области. SAVE fname.mat - сохраняет все переменные в файле fname.mal. SAVE data X Y Z - сохраняет переменные X, Y и Z в файле data-mal. SAVE fname X /ascii -переменная X сохраняется в ASCII формате.

SIN - вычисляет синус аргумента. SIN (X) - выдает вектор синусов элементов вектора X.

TEXT - TEXT(x,y,'string') печатает текст в кавычках на графическом экране, начиная с координаты (х,у) относительно последней поставленной точки.

TYPE - выводит на экран содержимое файла. Имя файла передается в качестве параметра (например^ТУРЕ odedemo.m).

WHILE - организует цикл с неопределенным количеством итераций. Синтаксис:

WHILE <переменная>,<оператор>;...;<оператор>; END Операторы выполняются пока в переменной не появится ноль.

WHO - выводит список имеющихся переменных.

XLABEL - XLABEL ( 'text' ) подписывает ось абсцисс текущего графика строкой « text».

YLABEL - YLABEL ( 'text' ) подписывает ось ординат текущего графика строкой «text».

Указанная функция решения дифференциальных уравнений имеет следующий заголовок:

[t,y]=ode23(FunName, t0, tfinal, y0, tol), trace);

FunName - имя функции, описывающей систему простых дифференциальных уравнений. Эта функция должна иметь следующий заголовок:

function yprime = fun(t,y), где FunName = 'fun' t - время (скаляр). у - вектор-столбец решений. yprime - возвращаемый вектор-столбец производных;

yprime(i)=dy(i)/dt

t0 - начальное значение времени tfinal - конечное значение времени

уО - вектор-столбец начальных значений производных (в момент t0) tol - задаваемая точность решений (по умолчанию tol=l.e-3) trace - флаг, регулирующий вывод промежуточных результатов (по умолчанию trace=0, что подавляет вывод)