
- •77 Ду. Занятия 9-13
- •Часть 2. Дифференциальные уравнения (ду) n-го порядка.
- •Занятие 9. Уравнения высших порядков. Уравнения, допускающие понижение порядка.
- •Занятие 10. Линейные ду n-го порядка. Линейная зависимость решений линейного уравнения. Линейное однородное уравнение.
- •Занятие 11. Линейные неоднородные уравнения с постоянными коэффициентами. Решение методами: «вариации произвольных постоянных» и «неопределенных множителей».
- •Занятие 12. Краевые задачи для линейных дифференциальных уравнений. Однородные и неоднородные уравнения Эйлера.
- •2). В записи уравнения 3-го порядка использование коэффициента позволяет получать результаты для уравнения 2-го порядка при значении .
- •Занятие 13. Уравнения n-го порядка. Контрольная работа №2. Прием части - 2 бдз. Выдача части - 3 бдз.
- •Часть 3. Системы линейных дифференциальных уравнений.
- •Занятие 15. Системы линейных однородных дифференциальных уравнений 1-го порядка с постоянными коэффициентами: общее и частное решения.
- •Занятие 16. Системы линейных неоднородных дифференциальных уравнений 1-го порядка с постоянными коэффициентами. Правая часть: специальная и произвольная.
- •Занятие 17. Повторение и систематизация материала. Подготовка к экзамену.
Занятие 16. Системы линейных неоднородных дифференциальных уравнений 1-го порядка с постоянными коэффициентами. Правая часть: специальная и произвольная.
|
Ауд. |
Л-2, Гл. 10 |
№ 441, 443, 445. |
3 |
☺ ☻ ☺
Общие
сведения. Как и прежде, в предлагаемых
для самостоятельных упражнений заданиях
мы ограничиваемся системами, состоящими
из двух уравнений. Поэтому все общие
выражения, применяемые при решении
систем уравнений, относим только к
системам двух дифференциальных уравнений:
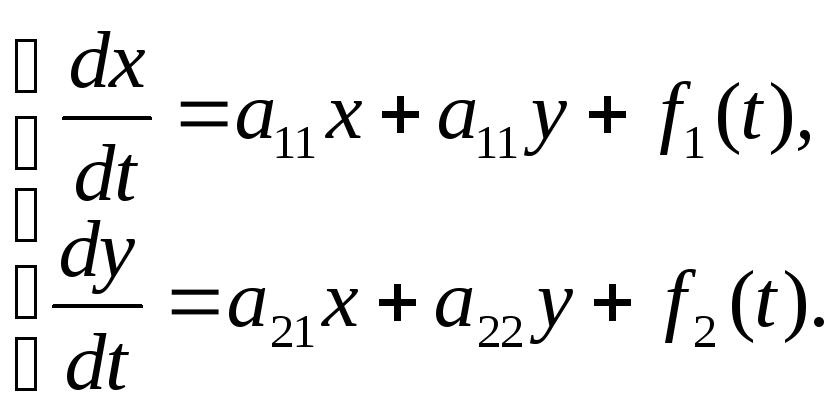 (1)
(1)
где
![]() –
действительные числа (постоянные);
функции
–
действительные числа (постоянные);
функции
![]() ,
,![]() – заданы;
– заданы;
![]() ,
,![]() – искомые, дифференцируемые функции.
– искомые, дифференцируемые функции.
Замечание:
многочлены
![]() ,
,
![]() ,
в общем случае имеют разные степени, в
частном случае это могут быть некоторые
числа.
,
в общем случае имеют разные степени, в
частном случае это могут быть некоторые
числа.
Если известно общее решение однородной системы уравнений, соответствующей системе (1) и некоторое частное решение неоднородной системы (1), то общее решение неоднородной системы записывают в виде:
![]() =
=![]() +
+![]() =
=![]() ·
·![]() +
+![]() ·
·![]() +
+![]() , (2)
, (2)
где обозначено:
![]() –
общее решение заданной системы (1) ,
–
общее решение заданной системы (1) ,
![]() –
общее решение соответствующей однородной
системы,
–
общее решение соответствующей однородной
системы,
![]() –
частное решение заданной системы
уравнений (1).
–
частное решение заданной системы
уравнений (1).
Так как задача
поиска решения
![]() подробно рассмотрена в разделе 3.2.
Остаётся рассмотреть задачу нахождения
решения
подробно рассмотрена в разделе 3.2.
Остаётся рассмотреть задачу нахождения
решения
![]() для случая, когда правая часть содержит
функции
для случая, когда правая часть содержит
функции
![]() ,
,![]() специального вида. Функция
специального вида. Функция
![]() называется специальной, если она
составлена из сумм и произведений
элементарных
функций:
называется специальной, если она
составлена из сумм и произведений
элементарных
функций:
▫
![]() –
многочлен степени
–
многочлен степени
![]() с коэффициентами в виде действительных
чисел.
с коэффициентами в виде действительных
чисел.
▫
![]() –
показательная
функция с основанием
–
показательная
функция с основанием
![]() ,
,
![]() –
действительное число.
–
действительное число.
▫
![]() ,
,![]() – функция с параметром
– функция с параметром
![]() –
действительное число.
–
действительное число.
Если функция
![]() =
=![]() ·
·![]() +
+![]() ·
·![]() ,
то необходимо учитывать некоторые
особенности,
возникающие при нахождении частного
решения
,
то необходимо учитывать некоторые
особенности,
возникающие при нахождении частного
решения
![]() :
:
1). Многочлены
![]() и
и
![]() в общем случае имеют разные степени, но
нас всегда будет интересовать
в общем случае имеют разные степени, но
нас всегда будет интересовать
![]() .
В частном случае возможно:
.
В частном случае возможно:
![]() =1,
или
=1,
или
![]() =0;
так же
=0;
так же
![]() =1,
или
=1,
или
![]() =0.
=0.
2). При значении
![]() =0
участие множителя
=0
участие множителя
![]() в записи
в записи
![]() явно не просматривается.
явно не просматривается.
3). При значении
![]() =0
участие множителей
=0
участие множителей
![]() ,
,![]() явно не просматривается.
явно не просматривается.
В любом случае для
нас важно определить по записи
![]() число
число
![]() =
=![]() –
образующее число
функции
–
образующее число
функции
![]() .
В частных случаях возможно:
.
В частных случаях возможно:
![]() =
=![]() и
и
![]() =
=![]() .
.
Поиск частного
решения
![]() проводится по тем же правилам, что и в
случае одного уравнения
проводится по тем же правилам, что и в
случае одного уравнения
![]() -
го порядка, но с некоторыми изменениями.
-
го порядка, но с некоторыми изменениями.
Так, если функция
![]() =
=![]() ·
·![]() +
+![]() ·
·![]() ,
то частное решение следует искать в
виде:
,
то частное решение следует искать в
виде: ![]() =
= ·
·![]() , (3)
, (3)
где
![]() ,
,![]() ,
,![]() ,
,![]() – многочлены степени
– многочлены степени
![]() =
=![]() ;
число
;
число
![]() – отражает кратность совпадения числа
– отражает кратность совпадения числа
![]() и характеристического корня
и характеристического корня
![]() системы; перечисленные многочлены
содержат неопределённые коэффициенты,
которые находят из тождеств, образующихся
после подстановки выражения:
системы; перечисленные многочлены
содержат неопределённые коэффициенты,
которые находят из тождеств, образующихся
после подстановки выражения:
![]() в систему (1).
в систему (1).
Завершается решение системы уравнений составлением её общего решения в соответствии с выражением (2).
Если функции
![]() ,
,![]() определяют несколько образующих чисел:
определяют несколько образующих чисел:
![]() =
=![]() ,
,
![]() =
=![]() ,..,
то в этом случае из совокупности функций
,..,
то в этом случае из совокупности функций
![]() ,
,![]() выделяют функции
выделяют функции
![]() ,
,
![]() ,..,
соответствующие числам
,..,
соответствующие числам
![]() ,
,![]() ..,
и для каждой из них находят частные
решения. В соответствии с теоремой
аддитивности частных решений записывают:
..,
и для каждой из них находят частные
решения. В соответствии с теоремой
аддитивности частных решений записывают:
![]() =
=![]() +
+![]() +… (4)
+… (4)
Приводимые ниже примеры иллюстрируют особенности решения неоднородных линейных систем дифференциальных уравнений со специальной правой частью.
••• ≡ •••
Пример
1–441:
Решить
систему нелинейных уравнений:
![]() (1)
(1)
Решение:
1). Найдем
характеристические корни соответствующей
однородной системы (т.е. без функции
![]() ):
):
![]() =
=
![]() = 0, откуда получаем:
= 0, откуда получаем:
![]() =–3;
=–3;
![]() =2.
В этом случае общее решение однородной
системы будем искать в виде:
=2.
В этом случае общее решение однородной
системы будем искать в виде:
![]() =
=![]()
![]() +
+![]()
![]() ,
(2)
,
(2)
где
![]() =
=![]() ∙e–3t=
∙e–3t=![]() ∙
∙![]() ,
,
![]() =
=![]() ∙e2t=
∙e2t=![]() ∙
∙![]() , (3)
, (3)
2). Для определения
векторов
![]() ,
,
![]() составим систему уравнений:
составим систему уравнений:
 (4)
(4)
Для корня
![]() =–3
система (4) имеет решение
=–3
система (4) имеет решение
![]() =
=![]() ;
для
;
для
![]() =2:
=2:
![]() =
=![]() .
.
Замечание: решение системы (4) проводится по известным правилам из курса «Линейная алгебра».
3). С учетом полученных
векторов
![]() ,
,
![]() запишем общее решение однородной системы
дифференциальных уравнений:
запишем общее решение однородной системы
дифференциальных уравнений: ![]() =
=![]() ∙
∙![]() ∙
∙![]() +
+![]() ∙
∙![]() ∙
∙![]() ,
(5)
,
(5)
4). Так как функция:
![]() – многочлен 1-й степени и образующее
число
– многочлен 1-й степени и образующее
число
![]() не совпадает с характеристическими
корнями:
не совпадает с характеристическими
корнями:
![]() и
и
![]() ,
то частное решение заданной системы
будем искать в виде:
,
то частное решение заданной системы
будем искать в виде: ![]() =
=![]() ,
ее производные:
,
ее производные:
![]() =
=![]() . (6)
. (6)
Подставляя (5) в
систему (1), получаем тождества:
![]() (7)
(7)
Приравнивая
коэффициенты при степенях
![]() и
и
![]() ,
получаем систему алгебраических
уравнений:
,
получаем систему алгебраических
уравнений:
1) при
![]() :
:
![]() 2) при
2) при
![]() :
:
![]() →
→
![]() =–
=–![]() ,
,![]() =–
=–![]() ,
,![]() =–
=–![]() ,
,![]() =–
=–![]() . (7)
. (7)
5). Запишем общее решение заданной неоднородной системы:
![]() =
=![]() +
+![]() =
=![]() ∙
∙![]() ∙
∙![]() +
+
![]() ∙
∙![]() ∙
∙![]() +
+
 .
(8)
.
(8)
Ответ:
общее решение системы:
![]() =
=![]() ∙
∙![]() ∙
∙![]() +
+![]() ∙
∙![]() ∙
∙![]() +
+ .
.
Пример
2–443:
Решить
систему нелинейных уравнений:
![]()
Решение:
При решении данного Примера воспользуемся теоремой о «суперпозиции» применения функций правой части и запишем две системы, эквивалентные данной, т.е. позволяющие получить общее решение исходной системы:
1a:
![]() →
число:
→
число:
![]() ,
1b:
,
1b:
![]() →
число:
→
число:
![]() .
.
1). Найдем
характеристические корни соответствующей
однородной системы (т.е. без функций
![]() ,
,![]() ):
):
![]() =
=
![]() = 0, откуда получаем:
= 0, откуда получаем:
![]() =
=![]() =2
– корень кратности
=2
– корень кратности
![]() .
В этом случае общее решение однородной
системы будем искать в виде:
.
В этом случае общее решение однородной
системы будем искать в виде:
 ,
и производные:
,
и производные:
 (2)
(2)
2). Подставляем (2) однородную систему для заданной системы и получаем тождества:
 (3)
(3)
3). Приравнивая в
(3) коэффициенты при степенях:
![]() и
и
![]() ,
получаем систему алгебраических
уравнений:
,
получаем систему алгебраических
уравнений:
 откуда
откуда
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]() =
=![]() . (4)
. (4)
Замечание: решение системы (4) проводится по известным правилам из курса «Линейная алгебра».
4). Итак, общее решение однородной системы уравнений получено:
 (5)
(5)
5). Частное решение
заданной системы уравнений, учитывая
системы (1a) и (1b),
запишем в виде:  , (6)
, (6)
6). Найдем частное
решение неоднородной системы уравнений
(1a), учитывая совпадение
числа
![]() с кратным характеристическим корнем:
с кратным характеристическим корнем:
 , (7)
, (7)
7). Подставим в (1a) выражение (7) и его производную: получим систему тождеств:

из которой найдем
неопределенные коэффициенты, приравнивая
коэффициенты при одинаковых степенях
![]() :
:
при
![]() :
: ![]() при
при
![]() :
:
![]() (8)
(8)
при
![]() :
: ![]() при
при
![]() :
:
![]()
откуда получаем:
![]() =
=![]() =
=![]() =
=![]() ,
,
![]() ,
,
![]() .
Учитывая выражение (7), получим частное
решение для системы (1a):
.
Учитывая выражение (7), получим частное
решение для системы (1a):
 . (9)
. (9)
8). Найдем частное
решение неоднородной системы уравнений
(1b), учитывая, что число
![]() не совпадает с характеристическим
корнем:
не совпадает с характеристическим
корнем:
 , (10)
, (10)
9). Подставим в (1 b) выражение (10) и его производную: получим систему тождеств:
![]() откуда: a=–3,
b=–2. (11)
откуда: a=–3,
b=–2. (11)
10). Учитывая выражение (10), получим частное решение для системы (1b):
 . (12)
. (12)
11). Учитывая (9) и (12), частное решение заданной системы уравнений принимает вид:
 , (13)
, (13)
12). Запишем общее решение заданной неоднородной системы:
 .
(14)
.
(14)
Замечание:
выражение (14) получено с «поглощением»
числа
![]() константой
константой
![]() .
.
Ответ:
Общее решение:
![]() =
=
 ∙
∙![]() .
.
Пример
3–445:
Решить
систему линейных уравнений:
![]()
Решение:
1). Найдем
характеристические корни соответствующей
однородной системы (т.е. без функций
![]() ,
,![]() ):
):
![]() =
=
![]() = 0, откуда находим:
= 0, откуда находим:
![]() =–i;
=–i;
![]() =i.
=i.
2). В этом случае общее решение однородной системы будем искать в виде:
![]() =
=![]()
![]() +
+![]()
![]() ,
(1)
,
(1)
где
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() ,
,
![]() =
=![]() ∙
∙![]() =
=![]() ∙
∙![]() , (2)
, (2)
3). Для определения
векторов
![]() ,
,
![]() составим систему уравнений:
составим систему уравнений:
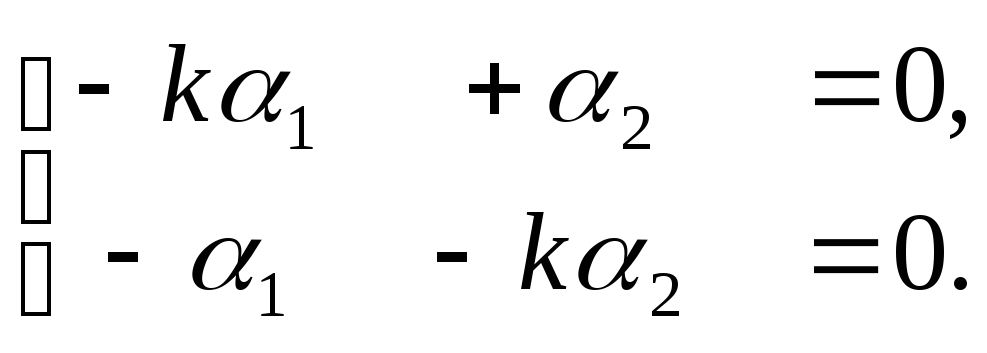 (3)
(3)
4). Для
![]() =–i
система (3) имеет решение:
=–i
система (3) имеет решение:
![]() .
Тогда можно записать:
.
Тогда можно записать:
 . (4)
. (4)
5). Для
![]() =i
система (3) имеет решение:
=i
система (3) имеет решение:
![]() .
Аналогично получаем:
.
Аналогично получаем:
 . (5)
. (5)
то есть решения
![]() и
и
![]() – комплексно-сопряженные.
– комплексно-сопряженные.
6). В качестве частных решений системы уравнений берем отдельно мнимую и действительную части. Получаем:
![]() =
=![]() ,
,
![]() =
=![]() (6)
(6)
7). С учетом выражений
(6) запишем общее решение однородной
системы дифференциальных уравнений:
![]() =
=![]()
![]() +
+![]()
![]() .
(7)
.
(7)
8). Для нахождения
искомых функций x(t),
y(t)
применяют метод «вариации произвольных
постоянных. Для этого считают
![]() ,
,
![]() функциями переменной
функциями переменной
![]() ,
которые находят из системы уравнений:
,
которые находят из системы уравнений:  или
или
 (8)
(8)
9). Так как определитель системы (3) не равен нулю, система имеет решение:
 или после
интегрирования:
или после
интегрирования:
 (9)
(9)
где
![]() ,
,
![]() – произвольные постоянные интегрирования.
Подставляя (9) в (7), получим общее решение
неоднородной системы уравнений:
– произвольные постоянные интегрирования.
Подставляя (9) в (7), получим общее решение
неоднородной системы уравнений:
![]() =
= =
= . (10)
. (10)
Ответ:
Общее решение:
![]() =
=
 .
.
☻
Вопросы для самопроверки:
-
Как по записи системы уравнений 1-го порядка определить, что она нелинейная?
-
Почему линейная система неоднородных уравнений с постоянными коэффициентами удовлетворяет требованиям теоремы «о существовании и единственности решений»?
-
Как записывают характеристический многочлен для системы линейных неоднородных уравнений с постоянными коэффициентами?
-
Как записывают общее решение системы линейных неоднородных уравнений с постоянными коэффициентами?
-
Как находят частное решение системы линейных неоднородных уравнений с постоянными коэффициентами в случае, если правая часть уравнений содержит специальные функции от независимой переменной?
-
Как находят частное решение системы линейных неоднородных уравнений с постоянными коэффициентами в случае, если правая часть уравнений содержит произвольные функции от независимой переменной?
Задачи для самоподготовки:
Пример
C16–1: Решить
систему нелинейных уравнений:
![]()
Ответ:
общее решение:
![]() =
=
 ∙
∙![]() .
.
Пример
C16–2: Решить
систему нелинейных уравнений:
![]()
Ответ:
общее решение:
![]() =
=
 ∙
∙![]() .
.
•• ☻☻ ••
