Занятие 13. Уравнения n-го порядка. Контрольная работа №2. Прием части - 2 бдз. Выдача части - 3 бдз.

☺ ☻ ☺

Контрольная работа №2 предназначена оценить степень усвоения основных понятий теории Дифференциальных уравнений и способов решения простейших типов ДУ n-го порядка:

• Линейные однородные уравнения n-го порядка с постоянными коэффициентами.

• Линейные неоднородные уравнения n-го порядка с постоянными коэффициентами и со специальной правой частью.

Состав и степень трудности предлагаемых в Контрольной работе заданий согласовывается с Методическим советом кафедры «Высшая математика».

При разработке заданий Контрольной работы учитывается также требование побудить студентов повторить пройденный материал по предмету. Это значит, что в заданиях не должно быть ничего такого, что, так или иначе, требует самостоятельных обобщений и выводов со стороны студентов.

Перед выполнением Контрольной работы студенты должны ознакомиться с перечнем вопросов, которые будут отражены в заданиях. Также важным элементом подготовки к контрольной работе должны быть регулярные текущие контрольные мероприятия в виде оперативных опросов: по 6-7 минут в начале каждого занятия.

Прием части-2 БДЗ определяется двумя последовательными мероприятиями:

1). Формальный приём выполненных Заданий непосредственно в аудитории: проверка на соответствие правилам закрепления вариантов заданий за каждым студентом.

2). Защита выполненных заданий БДЗ каждым студентом в специально назначенное время (обычно, в день консультаций по предмету). Определение окончательной оценки качества выполнения Части-2 БДЗ.

Замечание: 1). Сборник заданий по БДЗ находится в информационной системе института с самого начала семестра, постоянно.

2). Сборник заданий по БДЗ содержит по каждому заданию примеры решения и оформления.

•• ☻☻ ••

Часть 3. Системы линейных дифференциальных уравнений.

ЗАНЯТИЕ 14. Системы дифференциальных уравнений 1-го порядка. Сведение системы ДУ к одному уравнению высшего порядка

Ауд.

Л-2, Гл. 10

№ 412, 414, 416, 418, 420, 422*, 427.

7

☺ ☻ ☺

Общие сведения. Учитывая, что в предлагаемых для самостоятельных упражнений заданиях мы ограничиваемся системами, состоящими из двух уравнений, все общие выражения относим только к системам двух дифференциальных уравнений: (1)

где функции , – заданные, дифференцируемые.

Замечание: при ссылках на отдельные уравнения системы будем использовать двухпозиционные записи; например: (1.1) – ссылка на 1-е уравнение системы (1).

1). Продифференцируем уравнения (1.1) и (1.2) системы (1) по , учитывая, что – некоторые функции независимой переменной : . (2)

Воспользовавшись уравнениями (1.1) и (1.2), запишем выражение (2) в виде:

. (3)

2). Из выражений (1.1) и (3) составим систему уравнений: (4)

Для удобства, в системе уравнений (4) принято: , . Применяя общие правила решения системы уравнений, выразим (считая, что это возможно!) из уравнения (4.1) функцию и подставим её в уравнение (4.2):

. (5)

3). Уравнение (5) – дифференциальное уравнение 2-го порядка для функции . Решая это уравнение, получим: , (6)

где , – произвольные постоянные. Используя решение , вычисляем и записываем: .

4). Используя решения и , оформляем общее решение исходной системы (1).

••• ≡ •••

Пример 1–412: Решить систему уравнений: (1)

Решение:

Замечание: система уравнений не является линейной, применим метод сведения системы уравнений к одному уравнению 2-го порядка относительно или .

1). Продифференцируем по t уравнение (1.1): =–, учтём (1.2) → =–. Далее учитываем из (1.1): =, после чего получаем уравнение: , или . Последнее равносильно уравнению .

2). Интегрируя уравнение , получаем: =, или .

3). Учитывая уравнение (1.1), из выражения =получаем: .

4). Общее решение записывается в виде системы: .

Ответ: общее решение системы: .

Пример 2–414: Решить систему уравнений: (1)

Решение:

1). Умножив (1.1) на и учитывая (1.2), получим: . Интегрируя последнее, легко получаем: .

2). Перепишем (1.1), применяя тождественные преобразования: ==+. Учитывая (1.2), запишем: =+, или =–. Последнее уравнение легко интегрируется (если иметь в виду ): .

3). Используя выражения и , легко получить (сложив эти выражения!): . Модифицируя постоянные: → 2; → 2, запишем: . Возводя последнее выражение в квадрат, и учитывая выражение , получим: =. Используя , нетрудно получить =.

Замечание: Пример хорошо иллюстрирует возможности импровизации при решении системы ДУ применением метода сведения системы к одному уравнению высшего порядка.

Ответ: общее решение системы: .

Пример 3–416: Решить систему уравнений: 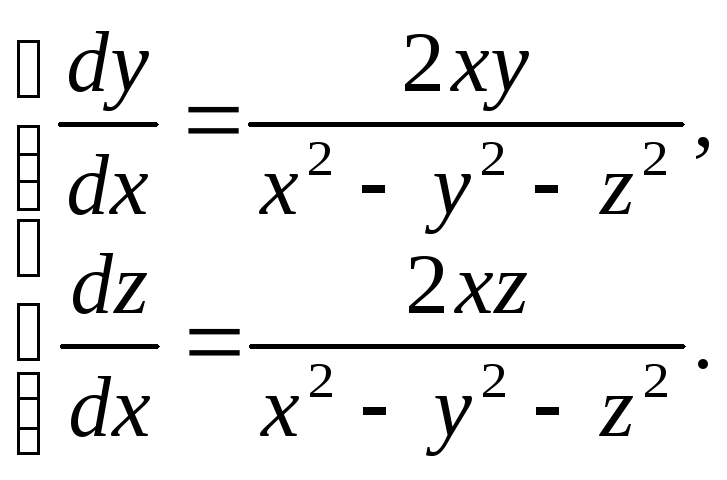(1)

Решение:

1). Из уравнения (1.1) получим: =, аналогично из (1.2): =. Эти два выражения дают: = → .

2). Учитывая , перепишем (1.1): = → =. Или в виде: = – однородное уравнение в стандартной форме. Его стандартное решение даёт: . Замечание: проверка условия: здесь не нужна из-за участия произвольной постоянной величины .

Ответ: общее решение системы: .

Пример 4–418: Решить систему уравнений: == (1)

Решение:

1). Из уравнения: =получаем: . Учитывая полученное выражение, запишем уравнение: = или: =1+.

2). Полученное уравнение стандартным алгоритмом приводится к уравнению с разделяющимися переменными! Пусть: , вычислим производную по переменной , имеем: . Тогда , окончательно: – переменные разделились! Интегрируя последнее, получаем выражение: , или .

Ответ: общее решение системы: , .

Пример 5–420: Найти общее и частное решения: , . (1)

Решение:

1). Продифференцируем уравнение (1.2): =–=. Учитывая уравнение (1.2) получим уравнение: , которое не содержит переменной и решается понижением порядка. → . Тогда имеем: , или (так как из уравнения (1.2): ) уравнение: – уравнение с разделяющимися переменными, откуда: и далее выражение: .

2). Дифференцируем выражение: и используем уравнение (1.2). Полученное выражение для функции : .

3). Общее решение уравнения: , .

4). Используя заданные начальные условия, имеем: , , откуда получаем величины , . Записываем частное решение: , .

Ответ: Частное решение: , .

Пример 6–422^*: Для системы уравнений: и функций и . проверить, являются ли соотношения первыми интегралами системы.

Решение:

Замечание: является первым интегралом системы , тогда и только тогда, когда: . (1)

1). Проверим уравнение (1) для функции : – тождественно. Является.

2). Проверим уравнение (1) для функции : . Не является.

Ответ: соотношение – является, а соотношение – не является.

Пример 7–427: Решить систему уравнений: (1).

Решение:

1). Перепишем уравнение (1.1): → . Для дальнейшего использования уравнение (1.2) запишем в виде: .

2). Продифференцируем уравнение (1.1): . Учитывая выражения для функции и для произведения , получим уравнение , которое после умножения на . принимает вид: – уравнение Эйлера. (2)

3). Применим подстановку: . Вычисляя производные , и учитывая уравнение (2), получаем уравнение: . Его корни: =, =.

4). Записываем ФСР: = и =. Общее решение: =.

5). Вычислим производную: . Учитывая полученное ранее выражение , получаем: =.

Ответ: общее решение системы =; =.

Замечание: обратим внимание на особенности применения способа решения системы ДУ сведением к уравнению высшего порядка для одной из искомых функций: здесь интенсивное применение средств математического анализа сочетается с достаточно тонкими средствами школьной алгебры!..

☻

Вопросы для самопроверки:

1. Что такое «нормальная форма» записи системы уравнений 1-го порядка?

2. Как уравнение n-го порядка представить в виде системы уравнений 1-го порядка?

3. Как систему уравнений 1-го порядка сводят к одному уравнению n -го порядка?

4. Как записывают начальные условия для системы трёх уравнений 1-го порядка?

Задачи для самоподготовки:

Пример C14–1: Решить систему уравнений: ==.

Ответ: общее решение системы: , .

Пример C14–2: Решить систему уравнений:

Ответ: общее решение: =, y==, .

Пример C14–3: Решить систему уравнений: ==.

Ответ: общее решение системы: , .

Пример C14–4: Решить систему уравнений:

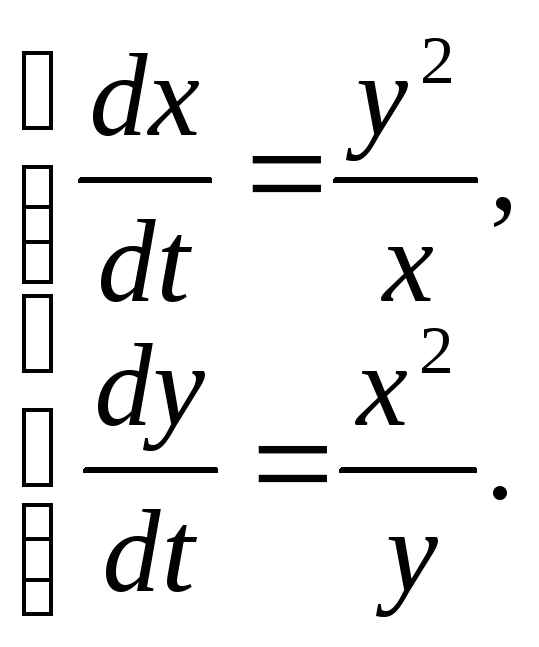
Ответ: общее решение системы: , .

Пример C14–5: Найти общее и частное решения: .

Ответ: общее решение: , . Частное решение: , .

Пример C14–6: Решить систему уравнений: .

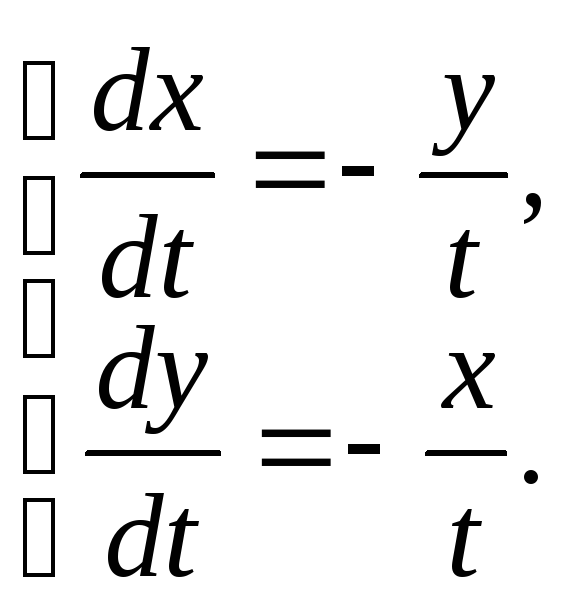Ответ: общее решение системы: =, =.

•• ☻☻ ••