§ 3. Уравнение Клеро.

В Главе 5 было рассмотрено уравнение Лагранжа , как одна из форм уравнения, не разрешённого относительно производной. В частном случае, когда , имеем:

. (1)

Уравнение (1) называют уравнением Клеро. Хотя для решения уравнения Клеро применяется тот же общий алгоритм поиска решения дифференциального уравнения в параметрической форме, особенности получаемых решений делают целесообразным рассмотрение уравнения Клеро особо.

Как и при решении уравнения Лагранжа, применим подстановку: =. С учётом подстановки перепишем уравнение (1): . (2)

Продифференцируем выражения (2) по переменной x , учитывая, что=(через посредство производной):. (3)

Учитывая, что =, перепишем (3):. Это значит, что возможны случаи:

, или . (4)

В случае: имеем решение=. Используя выражение (2), принимая=, запишем уравнение:. (5)

Выражение (5)– общий интеграл уравнения (1). С точки зрения геометрии полученное уравнение(5)определяет семейство кривых, а именно –семейство прямых линий.

Учитывая, что выражения (2) и (5) при значении =эквиваленты, запишем для уравнения Клеро систему, определяющую огибающую для семейства кривых (2):

Тождества (3) и (8) показывают, что у кривой семейства и огибающей общие точкаи касательная. Этот факт определяется системой уравнений:

общая запись: для уравнения Клеро:(6)

Система (6) для уравнения Клеро всегда определяет огибающуюлинию для семейства прямых линий, то естьособое решение, так как прямые семейства не имеют особых точек.

Убедимся, что система (6) определяет решение (особое) уравнения Клеро:

1). Запишем: и.

2). Запишем: ===– доказали.

3). Подставив в (1): =и, получим:, что совпадает с уравнением огибающей линии (6).

Исключив из системы уравнений (6) параметр =, получим решение уравнения Клеро , не содержащее . Это решение не может быть общим интегралом уравнения.

Решение: не является линейной функцией и потому не может быть получено из общего решения (ни при каком значении произвольной постоянной ).

С учетом совместного рассмотрения понятий: а) огибающая линия семейства кривых, б) общее решение, в) решение, не получающееся из общего ни при каком значении , уточним понятие особое решение:

Определение: (6.2)

Решение дифференциального уравнения, которое невозможно получить из общего интеграла ни при каком значении , и имеющее своим графиком огибающую линию семейства интегральных кривых, входящих в общее решение, называют особым решением дифференциального уравнения.

Анализируя предпринятые для нахождения решения уравнения Клеро шаги, запишем стандартный алгоритмего решения:

1). Примем: = и запишем общее решение уравнения (1): – семейство прямых линий.

2). Запишем систему, определяющую огибающую семейства прямых линий – особое решение уравнения Клеро:

общая запись: для уравнения Клеро:

3). Убедимся, что уравнение огибающей не может быть получено из общего решения за счёт выбора величины .

Рассмотрим несколько примеров решения уравнения Клеро: нахождение общего и особого решений.

☺☺

Пример 6–03: Задано уравнение: . Найти общее и особое решения уравнения.

Решение:

1). Заданное уравнение – уравнение Клеро. Примем: = и запишем общее решение заданного уравнения – семейство прямых линий. В нашем случае: .

2). Используя общую запись системы для огибающей линии: запишем систему для рассматриваемого примера в виде: , или в виде: Нетрудно, используя параметрическое задание огибающей линии, получить это уравнение в виде: – парабола.

3). Убеждаемся, что уравнение огибающей не может быть получено из общего решения за счёт выбора величины : за счёт выбора величины возможно только выделение из семейства прямых линий какой-то одной прямой, но не параболы! Значит, парабола есть особое решение (на рисунке выделена красным).

Ответ: общее решение: , особое решение: .

Пример 6–04: Задано уравнение: . Найти общее и особое решения уравнения.

Решение:

Замечание: Пример интересен тем, что заданное уравнение лишь незначительно отличается от рассмотренного выше примера!..

1). Заданное уравнение – уравнение Клеро. Примем: = и запишем общее решение заданного уравнения – семейство прямых линий. В нашем случае: .

2). Используя общую запись системы для огибающей линии: запишем систему для рассматриваемого примера в виде: , или в виде: 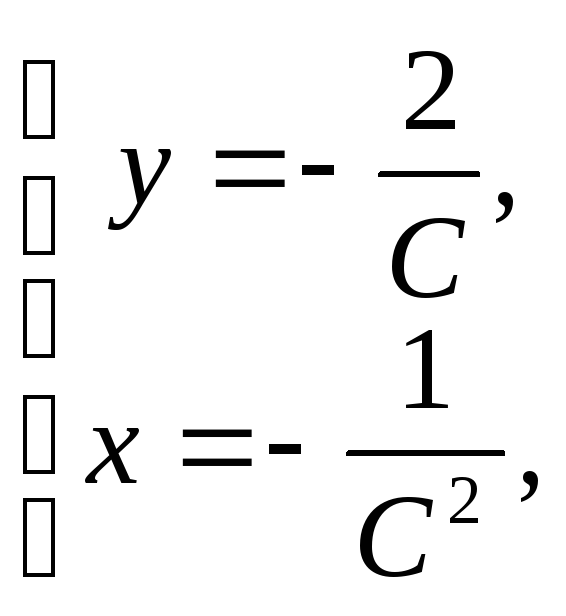Нетрудно, используя параметрическое задание огибающей линии, получить это уравнение в виде: – парабола.

3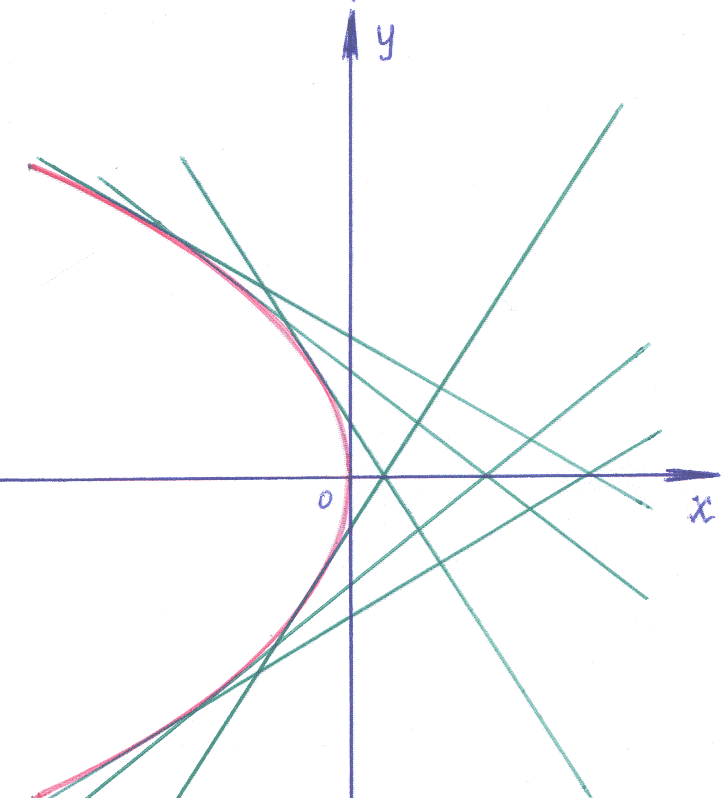). Убеждаемся, что уравнение огибающей не может быть получено из общего решения за счёт выбора величины : за счёт выбора величины возможно только выделение из семейства прямых линий какой-то одной прямой, но не параболы! Значит, парабола есть особое решение (на рисунке выделена красным).

Ответ: общее решение: , особое решение: .

Пример 6–05: Задано уравнение: . Найти общее и особое решения уравнения.

Решение:

1). Заданное уравнение – уравнение Клеро. Примем: = и запишем общее решение заданного уравнения – семейство прямых линий. В нашем случае: .

2). Используя общую запись системы для огибаю­щей линии: запишем систему для рассматриваемого примера в виде: , или в виде: Нетрудно, используя параметрическое задание огибающей линии, получить это уравнение в виде: – особое решение.

Замечание: В записи особого решения в логарифме переменная используется без модуля, так как (согласно параметрической записи уравнений системы) может принимать только положительные значения!..

3). Убеждаемся, что уравнение огибающей не может быть получено из общего решения за счёт выбора величины : за счёт выбора величины возможно только выделение из семейства прямых линий какой-то одной прямой, но кривой ! Значит, парабола есть особое решение (на рисунке выделена красным).

Ответ: общее решение: , особое решение: .

☻