
- •77 Ду. Занятия 9-13
- •Часть 2. Дифференциальные уравнения (ду) n-го порядка.
- •Занятие 9. Уравнения высших порядков. Уравнения, допускающие понижение порядка.
- •Занятие 10. Линейные ду n-го порядка. Линейная зависимость решений линейного уравнения. Линейное однородное уравнение.
- •Занятие 11. Линейные неоднородные уравнения с постоянными коэффициентами. Решение методами: «вариации произвольных постоянных» и «неопределенных множителей».
- •Занятие 12. Краевые задачи для линейных дифференциальных уравнений. Однородные и неоднородные уравнения Эйлера.
- •2). В записи уравнения 3-го порядка использование коэффициента позволяет получать результаты для уравнения 2-го порядка при значении .
- •Занятие 13. Уравнения n-го порядка. Контрольная работа №2. Прием части - 2 бдз. Выдача части - 3 бдз.
- •Часть 3. Системы линейных дифференциальных уравнений.
- •Занятие 15. Системы линейных однородных дифференциальных уравнений 1-го порядка с постоянными коэффициентами: общее и частное решения.
- •Занятие 16. Системы линейных неоднородных дифференциальных уравнений 1-го порядка с постоянными коэффициентами. Правая часть: специальная и произвольная.
- •Занятие 17. Повторение и систематизация материала. Подготовка к экзамену.
Занятие 10. Линейные ду n-го порядка. Линейная зависимость решений линейного уравнения. Линейное однородное уравнение.
|
Ауд. |
Л-2, Гл. 10 |
№ 207, 287, 301, 315, 317, 321, 323, 325, 333, 337. |
10 |
☺ ☻ ☺
Общие
сведения. При выполнении задания
необходимо знать, что характеристические
корни находят из характеристического
уравнения. Характеристическое уравнение
строят, формально заменяя в линейном
однородном дифференциальном уравнении
![]() -
го порядка с постоянными коэффициентами
производную
-
го порядка с постоянными коэффициентами
производную
![]() на степень
на степень
![]() :
:
![]()
![]()
![]() , (1)
, (1)
причем запись (1) можно реализовать в обоих направлениях: имея ДУ, построить характеристическое уравнение, и наоборот.
Если известны
корни характеристического уравнения:
![]() ,
можно восстановить характеристическое
уравнение (согласно известной теореме
алгебры о разложении многочлена
,
можно восстановить характеристическое
уравнение (согласно известной теореме
алгебры о разложении многочлена
![]() -
степени в произведение
-
степени в произведение
![]() линейных множителей):
линейных множителей):
![]() , (2)
, (2)
учитывая тождественность многочленов левой и правой частей (2).
Из школьной алгебры
наиболее известен частный случай записи
(2) для многочлена 2-й степени (теорема
Вьета): ![]() , (3)
, (3)
где
![]() и
и
![]() получены из тождественности левой и
правой частей выражения (3).
получены из тождественности левой и
правой частей выражения (3).
Если значение
коэффициента
![]() не задано, принимают
не задано, принимают
![]() =
1, что при выполнении заданий и следует
применять.
=
1, что при выполнении заданий и следует
применять.
Задача:
Пусть заданы
характеристические корни:
![]() некоторого дифференциального уравнения.
Имея эти корни, записать ДУ, для которого
числа
некоторого дифференциального уравнения.
Имея эти корни, записать ДУ, для которого
числа
![]() являются характеристическими корнями.
являются характеристическими корнями.
Далее выполняем стандартные действия:
1). Запишем характеристический многочлен, используя формальную запись:
![]() . (4)
. (4)
2). В выражении (4) раскрываем все скобки, приводим подобные члены и записываем характеристический многочлен, начиная со старшего члена по убыванию.
В результате выполнения этого действия, получаем характеристический многочлен:
![]() . (5)
. (5)
Замечание:
кому известны формулы Вьета для
коэффициентов многочлена
![]() -
степени, можно ими воспользоваться!
-
степени, можно ими воспользоваться!
3). Имея выражение
(5), строим ДУ, которому соответствует
данный характеристический
многочлен: ![]()
![]()
![]() . (6)
. (6)
Замечание: запись (6) можно прочитывать как слева направо, так и справа налево, что важно при решении дифференциального уравнения!
4). Записываем
ответ:
![]() – искомое дифференциальное уравнение.
– искомое дифференциальное уравнение.
Общие сведения. Наибольшие затруднения при решении дифференциального уравнения вызывает запись фундаментальной системы решений. Рассмотрим подробнее правила формирования ФСР по найденным характеристическим корням дифференциального уравнения:
1). Пусть
характеристические корни
![]() ,
,![]() и
и
![]() дифференциального уравнения -
действительные и различные. Для этих
корней можно записать три частных
решения ДУ
дифференциального уравнения -
действительные и различные. Для этих
корней можно записать три частных
решения ДУ
![]() ,
,
![]() и
и
![]() ,
которые независимы. Из этих решений
составляем ФСР (фундаментальную систему
решений), которая далее может использоваться
для записи общего решения.
,
которые независимы. Из этих решений
составляем ФСР (фундаментальную систему
решений), которая далее может использоваться
для записи общего решения.
2). Пусть
характеристические корни
![]() ,
,![]() и
и
![]() действительные, причем:
действительные, причем:
![]() =
=![]() =
=![]()
![]() .
Для этих корней можно записать три
частных решения ДУ
.
Для этих корней можно записать три
частных решения ДУ![]() ,
,
![]() и
и![]() ,
которые независимы. Из этих решений
составляем ФСР.
,
которые независимы. Из этих решений
составляем ФСР.
3). Пусть
характеристические корни
![]() ,
,![]() и
и
![]() действительные, причем
действительные, причем
![]() =
=![]() =
=![]() =
=![]() .
Для этих корней можно записать три
частных решения ДУ
.
Для этих корней можно записать три
частных решения ДУ
![]() ,
,
![]() и
и![]() ,
которые независимы. Из этих решений
составляем ФСР.
,
которые независимы. Из этих решений
составляем ФСР.
4). Пусть имеем
характеристические корни:
![]() -
действительный корень,
-
действительный корень,
![]() - пара комплексно-сопряженных корней.
Для корней
- пара комплексно-сопряженных корней.
Для корней
![]() ,
,![]() можно записать три частных решения ДУ
можно записать три частных решения ДУ![]() ,
,
![]() и
и
![]() ,
которые независимы. Из этих решений
составляем ФСР.
,
которые независимы. Из этих решений
составляем ФСР.
••• ≡ •••
Пример
1–207:
Имеем
семейство прямых линий (не параллельны
оси
![]() ):
):
![]() .
Найти дифференциальное уравнение, для
которого заданное семейство является
решением.
.
Найти дифференциальное уравнение, для
которого заданное семейство является
решением.
Решение:
1). Продифференцируем
заданное выражение:
![]() =
=![]() ,
далее
,
далее
![]() =0.
=0.
2). Уравнение
![]() =0:
и есть искомое ДУ.
=0:
и есть искомое ДУ.
Ответ: уравнение:
![]() =0.
=0.
Пример
2–287:
Исследовать
на линейную зависимость систему функций:
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]() .
.
Решение:
1). Для решения вопроса о независимости системы функций построим определитель Вронского:
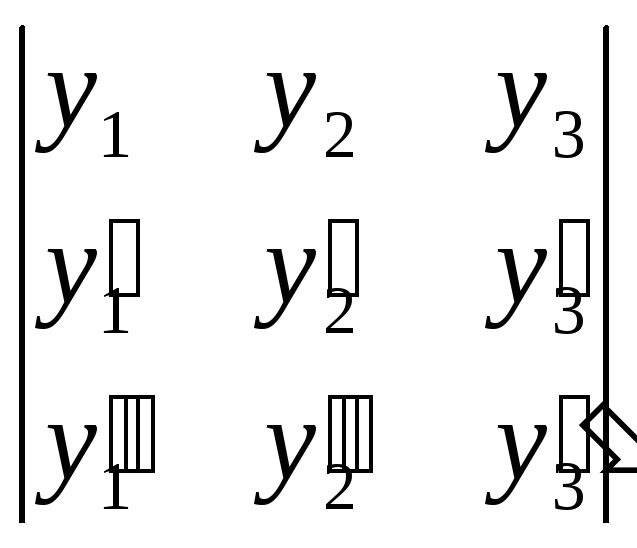 =
=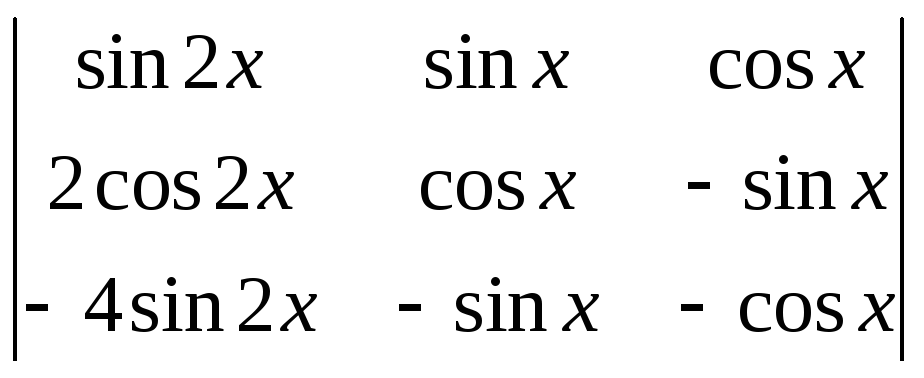 =
=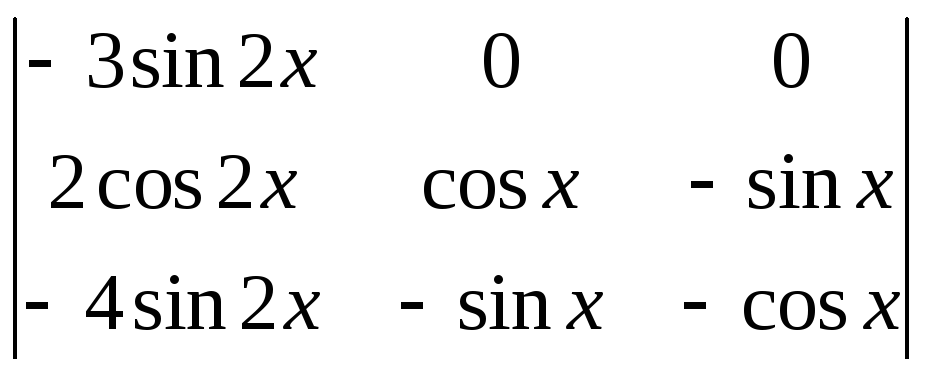 =
3
=
3![]() .
.
2). Видим: определитель Вронского не равен нулю. Значит, система функций линейно независима.
Ответ: система функций линейно независима.
Пример
3–301:
Имеем
фундаментальную систему решений (ФСР):
![]() =
=![]() ,
,
![]() =
=![]() ,
,
![]() =
=![]() линейного однородного уравнения.
Составить это уравнение.
линейного однородного уравнения.
Составить это уравнение.
Решение:
1). Проверим, являются
ли заданные функции независимыми, иначе,
могут ли они быть ФСР. Составим определитель
Вронского:
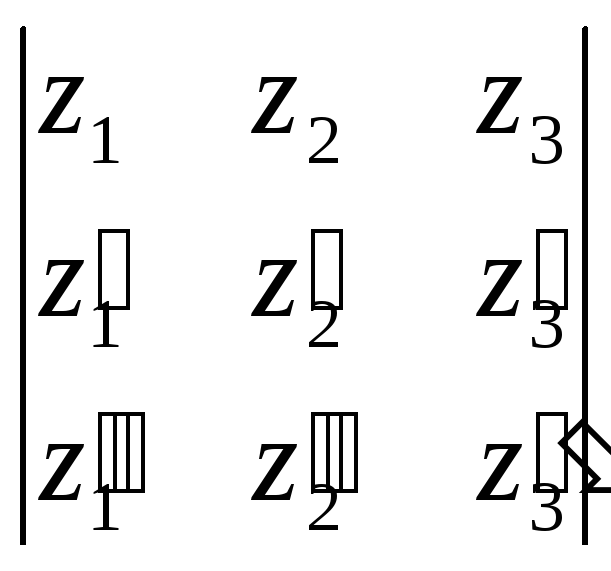 =
=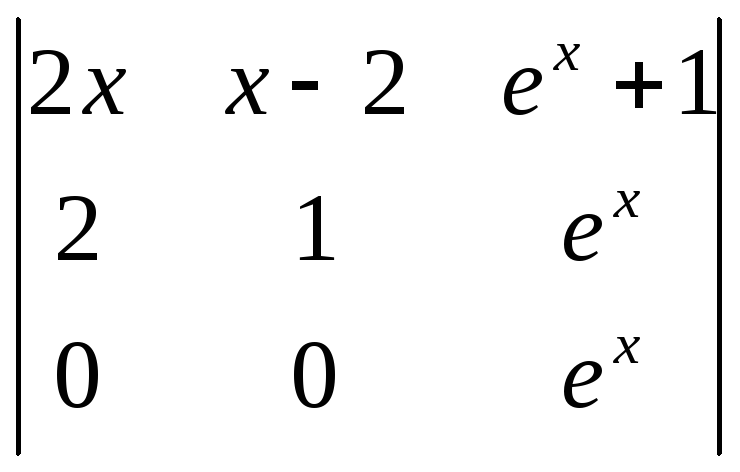 =
=![]() /
/
2). На самом деле
функции ФСР, соответствующие
характеристическим корням ДУ будут:
![]() =
1 =
=
1 =![]() – соответствует корень
– соответствует корень
![]() =0,
=0,
![]() =
=![]() =
=![]() – отмечает кратный корень
– отмечает кратный корень
![]() =0,
=0,
![]() =
=![]() – соответствует корень
– соответствует корень
![]() =1.
=1.
3). Составим
характеристический многочлен ДУ:
![]() =
=![]() =
=![]() =0.
По характеристическому многочлену
«восстанавливаем» искомое уравнение:
=0.
По характеристическому многочлену
«восстанавливаем» искомое уравнение:
![]() =0.
=0.
Ответ: уравнение:
![]() =0.
=0.
Пример
4–315:
По
данным корням:
![]() =3
и
=3
и
![]() =
–2 характеристического уравнения ЛОУ
с постоянными коэффициентами составить
ДУ и написать его общее решение.
=
–2 характеристического уравнения ЛОУ
с постоянными коэффициентами составить
ДУ и написать его общее решение.
Решение:
1). Учтем стандартную
запись уравнения 2-го порядка:
![]() .
.
2). В нашем случае
получим:
![]() .
.
3). Составляем ФСР:
![]() ,
,
![]() .
Общее решение:
.
Общее решение:
![]() =
=![]() .
.
Ответ:
дифференциальное уравнение:
![]() .
ФСР:
.
ФСР:
![]() ,
,
![]() .
Общее решение уравнения:
.
Общее решение уравнения:
![]() .
.
Пример
5–317:
По
данным корням:
![]() =
=![]() характеристического уравнения ЛОУ с
постоянными коэффициентами составить
ДУ и написать его общее решение.
характеристического уравнения ЛОУ с
постоянными коэффициентами составить
ДУ и написать его общее решение.
Решение:
1). Учтем стандартную
запись уравнения 2-го порядка:
![]() .
.
2). В нашем случае
получим:
![]() .
.
3). Составляем ФСР:
![]() ,
,
![]() и общее решение:
и общее решение:
![]() .
.
Ответ: уравнение:
![]() .
ФСР:
.
ФСР:
![]() ,
,
![]() .
Общее решение имеет вид:
.
Общее решение имеет вид:
![]() .
.
Пример
6–321:
Найти
общее решение ДУ:
![]() .
.
Решение:
1). Характеристическое
уравнение:
![]() ,
его корни:
,
его корни:
![]() ,
,
![]() .
.
2). Составляем ФСР:
![]() =
=![]() ,
,
![]() =
=![]() и общее решение:
и общее решение:
![]() .
.
Ответ: ФСР:
![]() =
=![]() ,
,
![]() =
=![]() .
Общее решение:
.
Общее решение:
![]() .
.
Пример
7–323:
Найти
общее решение ДУ:
![]() .
.
Решение:
1). Составим
характеристическое уравнение:
![]() ,
его корни:
,
его корни:
![]() =
=![]() =3.
=3.
2). Составляем ФСР:
![]() ,
,
![]() и общее решение:
и общее решение:
![]() .
.
Ответ: ФСР:
![]() ,
,
![]() .
Общее решение:
.
Общее решение:
![]() .
.
Пример
8–325:
Найти
общее решение ДУ:
![]() .
.
Решение:
1). Составим
характеристическое уравнение:
![]() ,
его корни:
,
его корни:
![]() =
=![]() .
.
2). Составляем ФСР:
![]() ,
,
![]() и общее решение:
и общее решение:
![]() .
.
Ответ: ФСР:
![]() ,
,
![]() .
Общее решение:
.
Общее решение:
![]() .
.
Пример
9–333:
Найти
общее решение ДУ:
![]() .
.
Решение:
1). Характеристическое
уравнение:
![]() ,
его корни:
,
его корни:
![]() =0,
=0,
![]() ,
,
![]() .
.
2). ФСР уравнения:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() и общее решение:
и общее решение:
![]() .
.
Ответ: ФСР:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
Общее решение:
.
Общее решение:
![]() .
.
Пример
10–337:
Найти
частное решение ДУ:
![]() ,
,
![]() ,
,
![]() .
.
Решение:
1). Составим
характеристическое уравнение:
![]() ,
его корни:
,
его корни:
![]() =1,
=1,
![]() =4.
=4.
2). Составляем ФСР:
![]() ,
,
![]() и общее решение:
и общее решение:
![]() =
=![]() .
Найдем производную:
.
Найдем производную:
![]() .
.
3). Для заданных
начальных условий:
![]() =
=![]() ,
,
![]() =
=![]() .
Находим:
.
Находим:
![]() =1,
=1,
![]() =0.
Следует частное решение:
=0.
Следует частное решение:
![]() .
.
Ответ: Частное
решение:
![]() .
.
☻
Вопросы для самопроверки:
-
Задано уравнение 2-го порядка. Как проверить, что функция
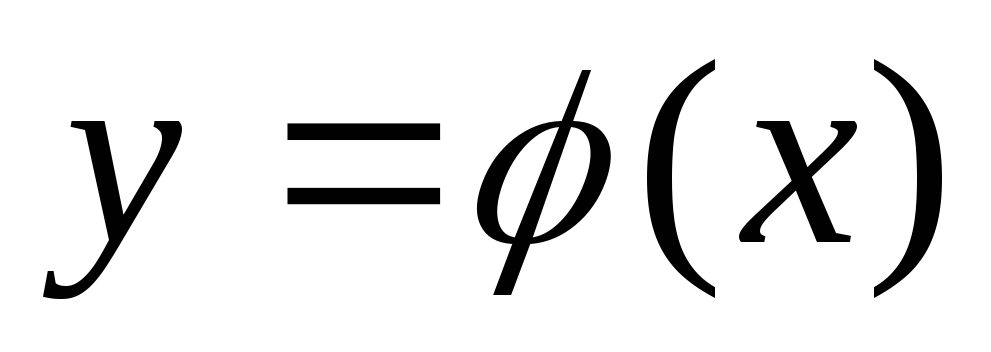 есть решение уравнения?
есть решение уравнения? -
Задано семейство кривых. Как найти уравнение, для которого семейство есть решение?
-
Имеем совокупность функций. Что значит: функции линейно зависимы?
-
Что такое «определитель Вронского»?
-
Как определить, зависимы или нет функции данной совокупности?
-
Что такое «фундаментальная система решений – ФСР»?
-
Может ли понятие ФСР применяться к неоднородным уравнениям?
-
Как записывают общее решение линейного однородного дифференциального уравнения?
-
Каковы свойства общего решения ДУ?
-
Что значит решить задачу Коши для ДУ второго порядка?
-
Какова роль определителя Вронского при решении задачи Коши для ДУ n-го порядка?
Задачи для самоподготовки:
Пример
C10–1: Показать,
что данное выражение:
![]() является решением дифференциального
уравнения:
является решением дифференциального
уравнения:
![]() при любых значениях
при любых значениях
![]() и
и
![]() .
.
Ответ:
тождество подтверждает:
заданное выражение есть решение
уравнения:
![]() .
.
Пример
C10–2: Имеем
семейство окружностей постоянного
радиуса:
![]() .
Найти дифференциальное уравнение, для
которого заданное семейство является
решением.
.
Найти дифференциальное уравнение, для
которого заданное семейство является
решением.
Ответ:
уравнение:
 .
.
Пример
C10–3:
Исследовать на линейную
зависимость систему функций:
![]() ,
,
![]() .
.
Ответ: система функций линейно независима.
Пример
C10–4: Имеем
фундаментальную систему решений (ФСР):
![]() ,
,
![]() линейного однородного
уравнения. Составить это уравнение.
линейного однородного
уравнения. Составить это уравнение.
Ответ:
уравнение:
![]() .
.
Пример
C10–5: Имеем
фундаментальную систему решений (ФСР):
![]() ,
,
![]() ,
,
![]() линейного однородного
уравнения. Составить это уравнение.
линейного однородного
уравнения. Составить это уравнение.
Ответ:
уравнение:
![]() .
.
Пример
C10–6: По
данным корням:
![]() =
=![]() =1
характеристического уравнения ЛОУ с
постоянными коэффициентами составить
ДУ и написать его общее решение.
=1
характеристического уравнения ЛОУ с
постоянными коэффициентами составить
ДУ и написать его общее решение.
Ответ:
уравнение:
![]() .
ФСР:
.
ФСР:
![]() ,
,![]() .
Общее решение:
.
Общее решение:
![]() .
.
Пример
C10–7:
Найти общее решение ДУ:
![]() .
.
Ответ:
ФСР:
![]() ,
,
![]() .
Общее решение:
.
Общее решение:
![]() .
.
Пример
C10–8:
Найти общее решение ДУ:
![]() .
.
Ответ:
ФСР:
![]() ,
,
![]() .
Общее решение:
.
Общее решение:
![]() .
.
Пример
C10–9:
Найти частное решение
ДУ:
![]() ,
,
![]() ,
,
![]() .
.
Ответ:
частное решение:
![]() .
.
•• ☻☻ ••
