|
Московский государственный институт электронной техники (технический университет) |
|
А. И. Литвинов
МЕТОДИЧЕСКОЕ ПОСОБИЕ для самостоятельной работы студентов (факультет ИТС)
|
|
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
|
|
Утверждено методическим советом кафедры ВМ-2 Зав. кафедры С. Г. Кальней
|
|
Россия, г. Москва 2012 г. |
А.И. Литвинов
ДИФФЕРЕНЦИАЛЬНЫЕ
УРАВНЕНИЯ
Учебное пособие по теории дифференциальных уравнений для студентов факультета итс миэт. Москва
2012
АННОТАЦИЯ
Пособие соответствует утверждённому Семестровому плану для студентов 1-го курса факультета ИТС и содержит систематизированный материал по теории «Дифференциальных уравнений».
Дифференциальные уравнения (сокращённо ДУ) – это область знаний, в которой объединяются знания из математического анализа, алгебры и аналитической геометрии. Из математического анализа активно используется умение дифференцировать функции одной и нескольких переменных, вычислять интегралы (в первую очередь, неопределённые). Из алгебры наиболее применяются разделы: тождественные преобразования, теория многочленов и линейная алгебра. Средства аналитической геометрии используются как для иллюстрации решений дифференциальных уравнений задач из физики и инженерной практики, так и для изучения свойств кривых линий в геометрических задачах.
В пособии представлены общие теоретические сведения о дифференциальных уравнениях и методы интегрирования отдельных типов уравнений первого и высших порядков, а также систем дифференциальных уравнений. Большое внимание уделено задачам из геометрии, механики, физики и техники, требующим составления и решения дифференциальных уравнений.
Изложение материала пособия построено таким образом, чтобы оказать студентам максимальную помощь при выполнении текущих заданий, заданий БДЗ, а также при подготовке к зачётам и экзаменам.
Оглавление
Стр.
Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8
Часть 1. Дифференциальные уравнения (ДУ) 1-го порядка.
Глава 1. Общие сведения. Теорема о существовании и единственности решения ДУ 1-го порядка. Уравнения первого порядка с разделяющимися переменными.
§ 1. Общие сведения. Теорема о существовании и единственности решения ДУ 1-го порядка . . . . 13
§ 2. Уравнения 1-го порядка с разделяющимися переменными . . . . . . . . . . . . . . . . . . . . . . . . . 18
§ 3. Применение уравнений с разделяющимися переменными: задачи из геометрии . . . . . . . 32
§ 4. Применение уравнений с разделяющимися переменными: задачи из физики . . . . . . . . . . 35
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 39
Глава 2. Однородные функции и однородные дифференциальные уравнения 1-го порядка.
§ 1. Однородные функции . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 40
§ 2. Однородные дифференциальные уравнения первого порядка . . . . . . . . . . . . . . . . . . . . . . . 42
§ 3. Уравнения специального вида, приводящиеся к однородному уравнению . . . . . . . . . . . . 47
§ 4. Обобщённые примеры решения уравнений специального вида . . . . . . . . . . . . . . . . . . . . . 49
§ 5. Применение однородных уравнений 1-го порядка: задачи из геометрии . . . . . . . . . . . . . . 50
§ 6. Применение однородных уравнений 1-го порядка: задачи из физики . . . . . . . . . . . . . . . . 53
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 54
Глава 3. Линейные дифференциальные уравнения 1-го порядка, уравнение Бернулли.
§ 1. Линейные дифференциальные уравнения 1-го порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . 55
§ 2. Уравнение Бернулли . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 60
§ 3. Применение линейных уравнений 1-го порядка в задачах геометрии . . . . . . . . . . . . . . . . 63
§ 4. Применение линейных уравнений 1-го порядка в задачах физики . . . . . . . . . . . . . . . . . . . 65
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 66
Глава 4. Дифференциальные уравнения в полных дифференциалах.
§ 1. Определение дифференциального уравнения в полных дифференциалах . . . . . . . . . . . . . 68
§ 2. Способ решения ДУ в полных дифференциалах и общий алгоритм решения . . . . . . . . . . 70
§ 3. Интегрирующий множитель . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 72
§ 4. Применение ДУ в полных дифференциалах: задачи из геометрии . . . . . . . . . . . . . . . . . . . 75
§ 5. Применение ДУ в полных дифференциалах: задачи из физики . . . . . . . . . . . . . . . . . . . . . 76
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 78
Глава 5. Уравнения первого порядка, не разрешенные относительно производной.
§ 1. Общие положения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 79
§ 2. Уравнения
первого порядка: многочлены
-
ой степени относительно
. . . . . . . . . . . . 79
§ 3. Уравнения,
разрешённое относительно
и не содержащее
. . . . . . . . . . . . . . . . . . . . . . 80
§ 4. Уравнения,
разрешённое относительно
и не содержащее
. . . . . . . . . . . . . . . . . . . . . . 82
§ 5. Уравнения, не
разрешённое относительно
и не содержащее
.
. . . . . . . . . . . . . . . . . . . 83
§ 6. Уравнения, не
разрешённое относительно
и не содержащее
.
. . . . . . . . . . . . . . . . . . . 84
§ 7. Уравнения Лагранжа . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
§ 8. Применение уравнений первого порядка, не разрешённых относительно производной:
задачи из геометрии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
− 4 −
§ 9. Применение уравнений первого порядка, не разрешённых относительно производной:
задачи из физики . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 90
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91
Глава 6. Семейство кривых линий и его «огибающая». Уравнение Клеро.
§ 1. Семейство кривых линий . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 93
§ 2. «Огибающая» семейства кривых линий . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 3. Особые решения дифференциального уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 4. Уравнение Клеро . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 5. Применение уравнений Клеро: задачи из геометрии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 6. Применение уравнений Клеро: задачи из физики . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Часть 2. Дифференциальные уравнения n-го порядка.
Глава 7. Уравнения высшего порядка. Уравнения, допускающие понижение порядка.
§ 1. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 2. Уравнения, допускающие понижение порядка . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 3. Применение уравнений, допускающих понижение порядка: задачи из геометрии . . . . . . 5
§ 4. Применение уравнений, допускающих понижение порядка: задачи из физики . . . . . . . . 5
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Глава 8. Линейные дифференциальные уравнения n-го порядка.
§ 1. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 2. Некоторые теоремы о решениях линейного уравнения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 3. Линейная зависимость решений линейного однородного уравнения . . . . . . . . . . . . . . . . . 5
§ 4. Линейные однородные уравнения с постоянными коэффициентами . . . . . . . . . . . . . . . . . 5
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Глава 9. Линейные неоднородные дифференциальные уравнения n-го порядка.
§ 1. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 2. Решение неоднородного уравнения методом «вариации произвольных постоянных» . . . 5
§ 3. Решение неоднородного уравнения методом «неопределённых коэффициентов» . . . . . . 5
§ 4. Применение линейных уравнений 2-го порядка: задачи из геометрии . . . . . . . . . . . . . . . . 5
§ 5. Применение линейных уравнений 2-го порядка: задачи из физики . . . . . . . . . . . . . . . . . . 5
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Глава 10. Однородные и неоднородные уравнения Эйлера.
§ 1. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 2. Однородное дифференциальное уравнение Эйлера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 3. Неоднородное дифференциальное уравнение Эйлера . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 4. Краевые задачи для линейных дифференциальных уравнений . . . . . . . . . . . . . . . . . . . . . . 5
§ 5. Применение уравнений Эйлера: задачи из геометрии . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 6. Применение уравнений Эйлера: задачи из физики . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
− 5 −
Часть 3. Системы линейных дифференциальных уравнений.
Глава 11. Системы дифференциальных уравнений первого порядка.
§ 1. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 2. Теорема о существовании и единственности решения системы уравнений . . . . . . . . . . . . 5
§ 3. Сведение системы ДУ к одному уравнению высшего порядка . . . . . . . . . . . . . . . . . . . . . . 5
§ 4. Механическая интерпретация системы уравнений 1-го порядка . . . . . . . . . . . . . . . . . . . . . 5
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Глава 12. Системы линейных однородных уравнений 1-го порядка с постоянными коэффициентами. Частное и общее решения системы.
§ 1. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 2. Частное решение системы линейных однородных дифференциальных уравнений
с постоянными коэффициентами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 3. Частное и общее решения системы линейных однородных уравнений 1-го порядка
с постоянными коэффициентами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Глава 13. Системы линейных неоднородных уравнений 1-го порядка с постоянными коэффициентами.
§ 1. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 2. Решение системы линейных неоднородных ДУ со специальной правой частью . . . . . . . . 5
§ 3. Решение системы линейных неоднородных ДУ с произвольной правой частью . . . . . . . . 5
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Глава 14. Элементы теории устойчивости.
§ 1. Общие сведения . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 2. Исследование устойчивости по первому приближению . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
§ 3. Исследование устойчивости методом функций Ляпунова . . . . . . . . . . . . . . . . . . . . . . . . . . 5
Вопросы для самопроверки . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
••• ≡ •••
− 6 −
|
ПРЕДИСЛОВИЕ |
При разработке настоящего пособия учитывалось, что студенты инженерных специальностей являются пользователями математических наук. Это значит, что при изучении любого вопроса теории дифференциальных уравнений мы руководствуемся двойственной педагогической задачей: с одной стороны, развивать и совершенствовать общую математическую культуру студента, а с другой стороны, нарабатывать навык практического использования приобретаемых знаний будущим инженером. Чтобы понять названную двойственность задачи преподавания теории дифференциальных уравнений, рассмотрим пример.
Известно,
что в общеобразовательной школе при
изучении простейшей системы линейных
уравнений вида
учитель, как правило, ставит перед собой
только одну цель – научить школьника
находить решения этой системы, применяя
простейший способ получения двух
уравнений, в каждое из которых входит
только одна неизвестная величина.
В институте, при изучении линейной алгебры, преподаватель знакомит студентов с множеством способов решения произвольных систем линейных неоднородных уравнений, показывая, что система двух уравнений с двумя неизвестными есть лишь частный случай общей задачи и что школьные знания отражают один из способов её решения. Как и школьный учитель, преподаватель института при изучении линейной алгебры не ставит перед собой цель – познакомить студентов с практическими задачами, которые порождают системы линейных уравнений.
При
изучении аналитической геометрии
преподаватель применяет систему линейных
уравнений вида:
как математическую модель пары прямых
на плоскости
для исследования их взаимного расположения.
Это становится выразительным образом
практического применения абстракций
алгебры в геометрии.
При
изучении линейного программирования
система уравнений
отражает процесс распределения некоторого
ресурса
в количествах
и
между двумя потребителями
и
согласно двум стратегиям:
и
.
В этом случае математическая модель
ещё более выразительно иллюстрирует
практическую ценность математики.
Рассмотренный пример показывает, как при изучении систем линейных уравнений у учащегося может сформироваться ложное представление: математики придумали разные системы уравнений и теперь учат их решать.
В настоящее время практика применения теории дифференциальных уравнений в различных областях науки и техники настолько богата, что изучение любого вопроса теории по отношению к конкретному уравнению можно начинать с практической задачи, вызвавшей появление этого уравнения. Более того, изучение каждого теоретического вопроса будет ещё более успешным, если его завершить известными задачами из геометрии и физики!
Автор надеется, что настоящее пособие, реализуя поставленную педагогическую задачу, сможет максимально помочь будущим инженерам в освоении теории и практики дифференциальных уравнений.
− 7 −
|
ВВЕДЕНИЕ |
Приступая к изучению теории «Дифференциальных уравнений», вспомним некоторые сведения из математического анализа, а именно:
1). Если
на некотором интервале
функция
дифференцируема, то имеют в виду, что
на этом интервале существует производная
этой функции
.
Используя последнее выражение, можем
записать
– дифференциал
функции
.
Замечание:
В математическом анализе получены
выражения для производных всех часто
используемых функций и составлены
таблицы: [функция
]
→
[производная
].
Если эту таблицу применять формально,
то можно считать, что определено
соответствие
(отображение):
,
или
– дифференцирование.
2). Если
на некотором интервале
имеем производную некоторой функции
,
то можно найти выражение этой функции
,
которую в этом случае называют
первообразной
для функции
.
Процесс нахождения первообразной для
функции
условно (для краткости) представили в
виде записи:
=
+
– неопределённый
интеграл.
Замечание:
В математическом анализе для первообразных
всех часто используемых функций
составлены таблицы: [производная
]
→
[первообразная
=
+
].
Если эту таблицу применять формально,
то можно считать, что определено
соответствие
(отображение):
– интегрирование,
то есть применение неопределённого
интеграла к функции
.
Названные сведения из математического анализа попробуем применить для решения известных в элементарной физике задач:
1) нахождение закона свободного падения тела в поле тяготения Земли;
2) нахождение закона изменения давления в атмосфере Земли в зависимости от высоты над уровнем моря.
Пример
1.
Материальная точка массы
свободно падает под действием силы
тяжести
.
Найти закон движения этой точки.
Сопротивление воздуха не учитывать.
Р
ешение:
1).
Известно, что движение определяется по
отношению к некоторой системе отсчёта.
Для рассматриваемой задачи удобно в
качестве системы отсчёта принять
неподвижную относительно Земли числовую
ось
,
направленную в сторону падения
материальной точки, то есть вертикально
вниз. Такую систему отсчёта считают
инерциальной!
2).
Учитывая допущение, что сопротивление
воздуха не учитывается, в соответствии
со вторым законом Ньютона, запишем:
,
где
– ускорение тела под действием силы
тяготения Земли
.
Так как
=
,
где
– ускорение свободного падения тела в
поле тяготения Земли, запишем:
,
или
.
3).
Учтём, что ускорение
,
где
– скорость движения тела. Перепишем
уравнение
в виде:
.
− 8 −
Обычно
рассматривают падение тела с небольшой
(по сравнению с радиусом Земли) высоты
и принимают
.
Применяя понятие первообразной для
функции
,
запишем:
,
где
– произвольная постоянная величина.
Используя таблицу неопределённых
интегралов, получаем:
– закон движения тела при свободном
падении, где переменная
отражает время от начала падения тела.
Если известно, что в момент времени
скорость тела вдоль оси
была равной
,
говорят, что заданы начальные
условия движения:
.
Для этого случая можем записать:
=
,
откуда вычисляем:
.
Используя значение
,
запишем:
– закон движения тела при свободном
падении для заданных начальных условий
(хорошо известное в элементарной физике
выражение). Если начальные условия
заданы для
=0,
то есть:
,
закон свободного падения тела определяется
выражением
.
В задачах элементарной физике часто
применяют условие:
,
тогда
– самое простое выражение для закона
свободного падения тела.
4).
Известно,
что скорость
движения тела может быть определена
как производная перемещения этого тела:
.
Это значит:
=
,
что в общем виде можно записать:
.
Интегрируя выражение:
=
,
получим:
,
где
– произвольная постоянная величина.
Используя таблицу неопределённых
интегралов, получаем:
– закон движения тела при свободном
падении, где переменная
отражает время от начала падения тела.
Исходя
из физического смысла рассматриваемой
задачи, заметим, что в этом случае
движение будет полностью определено,
если для момента времени
заданы начальные условия в виде:
и
.
Учитывая значение величины
для заданных начальных условий, именно:
,
выражение
запишем в виде:
.
Заменяя в выражении:
значения
и
,
после несложных тождественных
алгебраических преобразований получим:
– закон движения тела при свободном
падении для заданных начальных условий
(хорошо известное в элементарной физике
выражение). Если начальные условия
заданы для
=0,
то есть:
и
,
закон свободного падения тела определяется
выражением
.
Если
и
,
получим:
.
Закон свободного падения тела определяется
самым простым выражением:
,
когда
и
.
Выводы:
а). Моделирование
законов свободного падения тела
потребовало применения производных:
и
.
Интегрирование функции
вызвало появление произвольной постоянной
в выражении для функции
.
Второе интегрирование позволило получить
выражение для функции
и появление второй произвольной
постоянной
.
б). Учитывая
присутствие в выражении:
произвольной постоянной величины
,
будем решение
называть общим
решением
задачи для закона скорости движения
тела.
− 9 −
в). Учитывая
присутствие в выражении:
произвольных постоянных величин
и
,
решение
будем называть общим
решением
задачи для закона перемещения тела.
г). Применение
начальных условий:
и
позволяет находить частные
решения
задачи исследования свободно падающего
тела.
Ответ:
общее решение:
,
частное решение:
.
Отметим
особенность Примера 1: после того, как
было принято допущение
,
решения в форме:
и
в элементарной физике были достаточно
просто получены без использования
понятия первообразной, то есть понятия
неопределённого интеграла. В этом
особенная ценность рассмотренного
примера: знакомый результат получен
применением нового инструмента, причём
в этом случае мы обошлись без тонких
рассуждений, которые были использованы
в элементарной физике.
Пример 2. Определить давление воздуха атмосферы Земли в зависимости от высоты над уровнем моря.
Р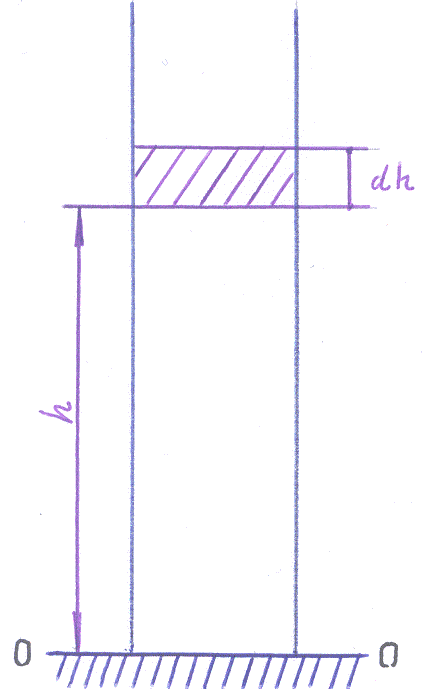
ешение:
1).
На рисунке уровень моря отмечен линией
.
Обозначим давление воздуха на этом
уровне величиной
.
На высоте
над уровнем моря давление будет
=
– искомая функция.
2).
Рассмотрим прямую призму, основание
которой имеет площадь
=
.
Известно, что на уровне моря (где
=0)
давление воздуха
=
1
.
При этом давлении объём воздуха
=
весит
(H).
Воспользуемся законом Бойля-Мариотта:
.
Это значит, что на высоте
при давлении
то же количество воздуха будет занимать
объём:
.
В таком случае вес
воздуха на высоте
будет
,
где
– коэффициент пропорциональности.
3).
На
высоте
в рассматриваемой призме выделим слой
воздуха, толщина которого равна:
.
Вес этого слоя равен
.
Обозначим разность давлений верхнего
и нижнего сечений выделенного слоя
величиной
.
Из условия равновесия выделенного слоя
воздуха можем записать:
=
,
или
.
Применяя понятие первообразной для
функции:
,
получим:
.
Известно:
=
(здесь
).
Тогда:
=
.
Так как нужна зависимость
=
,
из последнего выражения запишем:
.
Используя начальные условия: при
=0
имеем
,
получим:
.
− 10 −
Ответ:
зависимость давления от высоты:
.
Выводы:
а). Моделирование
зависимости давления атмосферы Земли
от высоты потребовало применения
производной
.
Интегрирование функции
вызвало появление произвольной постоянной
в выражении:
.
б). Учитывая
присутствие в выражении:
произвольной постоянной величины
,
будем решение
называть общим
решением
задачи.
в). Применение
начальных условий:
позволяет находить частные
решения
задачи.
Ценность
Примера 2 в том, что закон изменения
давления атмосферы Земли в зависимости
от высоты над уровнем моря получен
формальным применением понятия
первообразной для функции:
,
полученной применением простейшего
физического закона – закона статики.
В элементарной физике закон
использовался без доказательства.
Что
общего в рассмотренных задачах?
Для ответа на этот вопрос воспользуемся
традиционными обозначениями:
− независимая переменная,
−
функция переменной
,
−
производная функции
1-го порядка,
−
производная функции
2-го порядка. Тогда можем заметить:
1). При
нахождении закона
использовалось уравнение в виде:
как частный случай общего выражения
.
2). При
нахождении закона
использовалось уравнение:
как частный случай общего выражения
.
При нахождении закона
использовалось уравнение в виде:
как
частный случай общего выражения
.
В теории
дифференциальных уравнений уравнение
,
причём присутствие в уравнении производной
обязательно, называют дифференциальным
уравнением 2-го порядка. Аналогично,
уравнение
=0,
причём присутствие в уравнении производной
обязательно, называют дифференциальным
уравнением 1-го порядка. Теперь можем
ответить на поставленный вопрос – во
всех рассмотренных задачах из физики
для нахождения физических законов мы
решали дифференциальные уравнения!
Надеемся, что рассмотренные примеры помогут студентам уже на первых шагах изучения теории дифференциальных уравнений почувствовать огромные возможности этой теории в познании сложных явлений и процессов в разных областях науки и техники.
• ◄ ≡ ► •