4.2. Линейные однородные уравнения n-го порядка.
Пусть задано
линейное однородное уравнение n-го
порядка с постоянными коэффициентами:
. (27)
Учитывая опыт
решения дифференциального уравнения
2-го порядка, решение уравнения (26) будем
искать в виде:
=
.
Подставляя эту функцию в уравнение
(26), получимхарактеристическое
уравнение:
. (28)
Корни этого уравнения называют характеристическими корнямидифференциального равнения (27). Общие правила вычисления корней уравнения (28) можно найти в разделе Многочлены в курсе высшей алгебры (конечно, в первую очередь используем знания из элементарной алгебры).
Учитывая различные Случаи вычисления характеристических корней уравнения (27), запишем общий алгоритмпостроениявсех независимыхрешений для этого уравнения:
1). Для действительного
корня
кратности 1 записываем частное решение:
=
.
2). Для каждого
действительного корня
кратности
записываем
частных решений:
=
,
=
,
=
,…,
=
.
(29)
3). Для каждой пары
=
комплексно-сопряженных корней кратности
1 записываем пару частных решений:
=
и
=
.
4). Для каждой пары
комплексно-сопряженных корней
кратности
записываем
пар частных решений:
=
,
=
,
=
,…,
=
; (30)
=
,
=
,
=
,…,
=
; (31)
=
,
=
,
=
,…,
=
.
Завершив построение
всех
независимых решений, получают ФСР и
далее общее решение уравнения
(27):
=
. (32)
В записи общего
решения уравнения (27) произвольные
постоянные:
обеспечивают решение задачи Коши для
начальных условий:
,
=
,...,
=
.
Замечание: Зная корни характеристического уравнения, легко записать характеристическое уравнение (28), определяющее эти корни (используют теорему Безу), а затем дифференциальное уравнение (27).
§ 6. Обобщающие примеры по теме: линейные однородные уравнения.
Набор обобщающих Примеров, представленных ниже, предназначен оказать максимальную помощь студентам, испытывающим трудности при изучении темы: Линейные однородные уравнения.
☺ ☻ ☺
Пример 8–01:
Имеем
семейство парабол с осью, параллельной
оси
.
Найти дифференциальное уравнение, для
которого заданное семейство является
решением.
Решение:
Замечание: определение семейства парабол допускает два случая его аналитического представления; рассмотрим оба!
Случай-1.
Семейство парабол задано в виде функции:
.
1).
Вычислим производные заданной функции:
=
,
=
.
2).
Запишем выражение:
=
,
то есть получено выражение, в которое
не входят
параметры
и
семейства парабол. Значит
– дифференциальное уравнение 2-го
порядка, определяющее семейство парабол
.
Случай-2.
Семейство парабол задано в виде функции:
.
1).
Вычислим производные заданной функции:
=
,
=
,
=0.
2).
Получено выражение:
=0,
то есть выражение, в которое не входят
параметры
,
и
семейства парабол. Значит
=0
– дифференциальное уравнение 3-го
порядка, определяющее семейство парабол
.
Ответ:
уравнение может быть записано в виде:
,
или в виде:
=0.
Замечание: Обратили внимание на факты. Если семейство кривых определяют 2 параметра, его определяет дифференциальное уравнение 2-го порядка. Если семейство кривых определяют 3 параметра, его определяет дифференциальное уравнение 3-го порядка!
Пример 8–02:
Имеем фундаментальную систему решений
(ФСР):
=
,
=
,
=
линейного однородного уравнения.
Составить это уравнение.
Решение:
1). Для решения вопроса о независимости системы функций построим определитель Вронского:
=
=
.
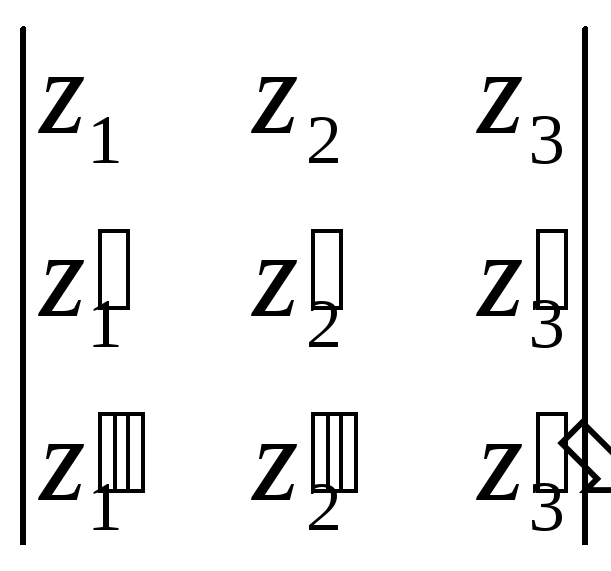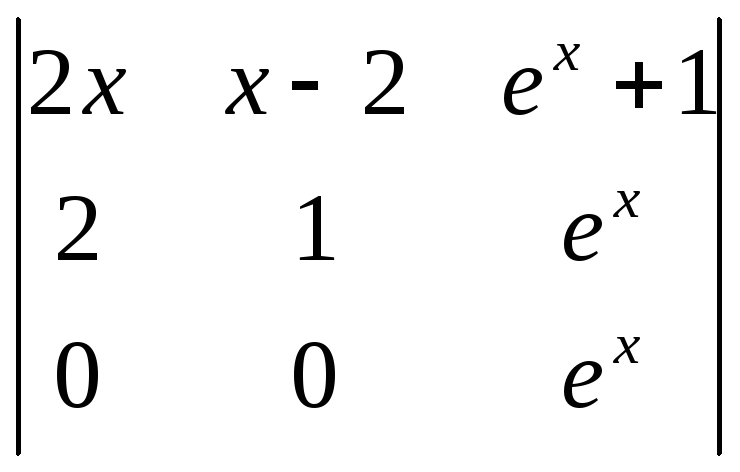2).
Видим: определитель Вронского не равен
нулю. Это значит, что заданная совокупность
функций линейно независима для любых
значений 
.
3). На самом деле
функции ФСР, соответствующие
характеристическим корням ДУ будут:
=
1 =
– соответствует корень
=0,
=
=
– отмечает кратный корень
=0,
=
– соответствует корень
=1.
4). Составим
характеристический многочлен ДУ:
=
=
=0.
По характеристическому многочлену
«восстанавливаем» искомое уравнение:
=0.
Ответ: уравнение:
=0.
Пример 8–03:
Найти
общее решение ДУ:
.
Решение:
1). Составим
характеристическое уравнение:
,
его корни:
=
=3.
2). Составляем ФСР:
,
и общее решение:
.
Ответ: ФСР:
,
.Общее решение:
.
Пример 8–04:
Найти
общее решение ДУ:
.
Решение:
1). Составим
характеристическое уравнение:
,
его корни:
=
.
2). Составляем ФСР:
,
и общее решение:
.
Ответ: ФСР:
,
.Общее решение:
.
Пример 8–05:
Найти
общее решение ДУ:
.
Решение:
1). Характеристическое
уравнение:
,
его корни:
=0,
,
.
2). ФСР уравнения:
,
,
,
,
и общее решение:
.
Ответ: ФСР:
,
,
,
,
.Общее решение:
.
Пример 8–06:
Найти
частное решение ДУ:
,
,
.
Решение:
1). Составим
характеристическое уравнение:
,
его корни:
=1,
=4.
2). Составляем ФСР:
,
и общее решение:
=
.
Найдем производную:
.
3). Для заданных
начальных условий:
=
,
=
.
Находим:
=1,
=0.
Следует частное решение:
.
Ответ: Частное
решение:
.
Пример 8–07:
Показать,
что данное выражение:
является решением дифференциального
уравнения:
при любых значениях
и
.
Решение:
1). Дифференцируем
заданное выражение:
,
или
.
2). Далее дифференцируем:
.
3). Подставим
найденные производные в уравнение
:
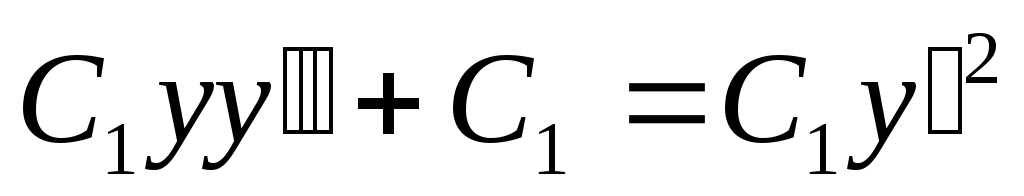–тождество.
Ответ: тождество
подтверждает: заданное выражение есть
решение уравнения:
.
Пример 8–08:
Имеем
семейство окружностей постоянного
радиуса:
.
Найти дифференциальное уравнение, для
которого заданное семейство является
решением.
Решение:
1). Дифференцируем
заданное выражение:
,
далее
.
2). Получили систему уравнени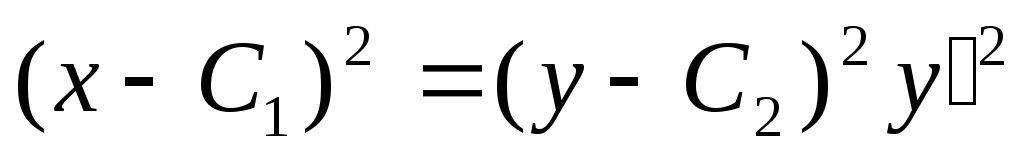й:
;
и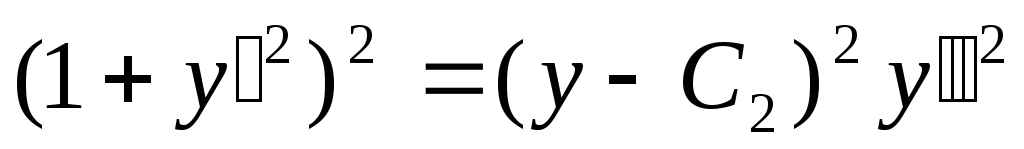
.
Решая систему,
получаем:
,
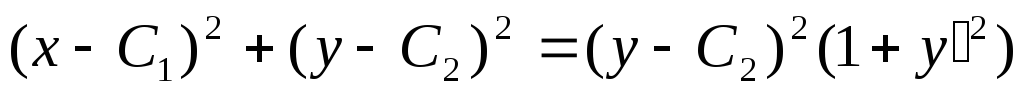или
.
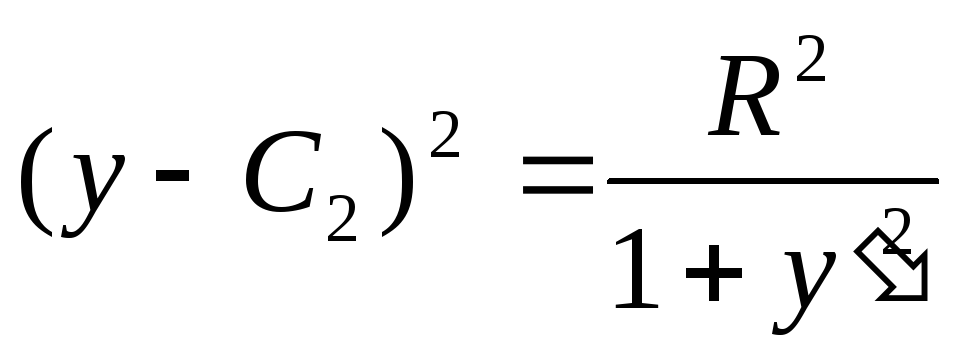3). Учитывая
,
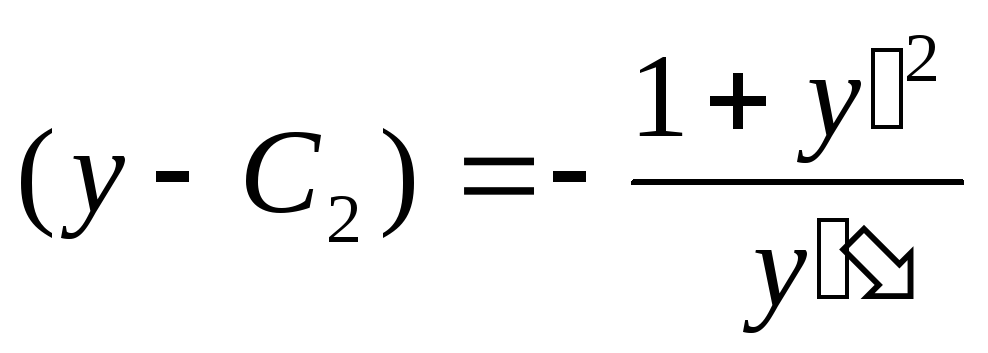запишем уравнение:
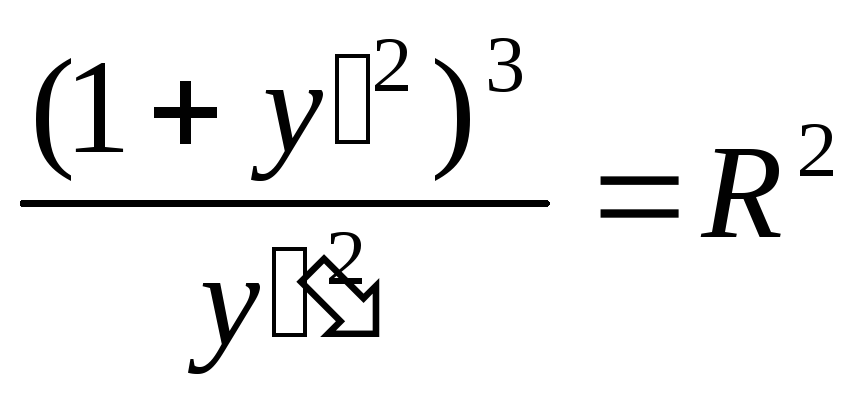– искомое ДУ.
Ответ: уравнение:
.
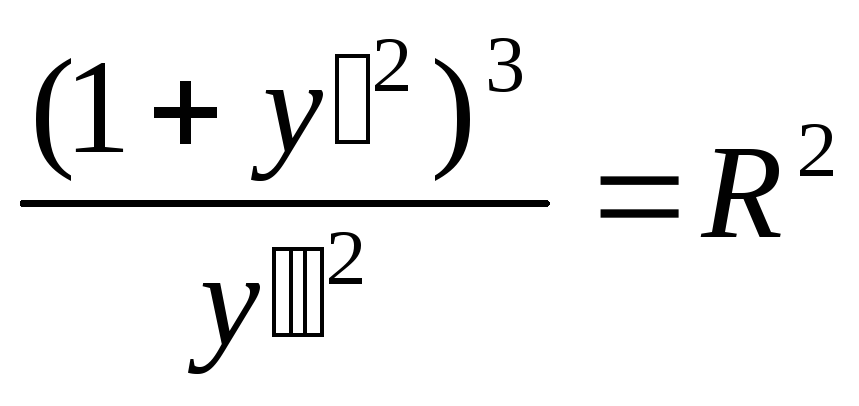Пример 8–09:
Исследовать
на линейную зависимость систему функций:
,
.
Решение:
1). Для решения
вопроса о независимости системы функций
построим определитель Вронского:
=
=
.
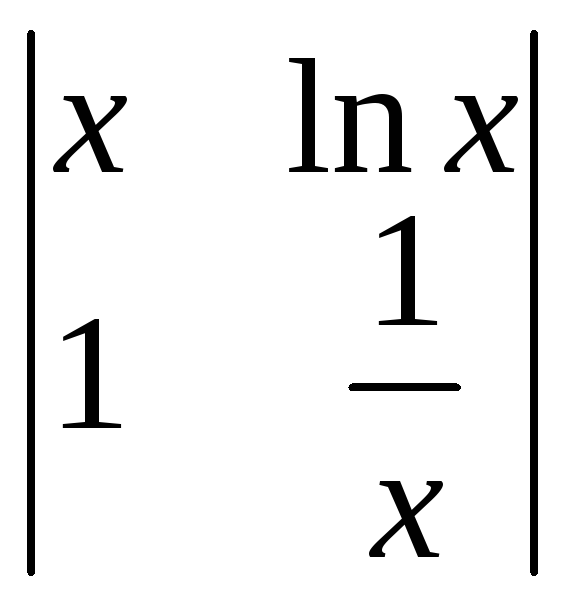2). Видим: определитель Вронского не равен нулю. Значит, система функций линейно независима.
Ответ: система функций линейно независима.
Пример 8–10:
Имеем
фундаментальную систему решений (ФСР):
,
линейного однородного уравнения.
Составить это уравнение.
Решение:
1). Имея решение
уравнения:
,
учтем: 1 =
→
=0.
Также:
→
=–1.
2). Имея корни
,
,
восстановим характеристический
многочлен:
,
или
.
4). Имея
характеристический многочлен, восстановим
ДУ:
.
Ответ: уравнение:
.
Пример 8–11:
Имеем
фундаментальную систему решений (ФСР):
,
,
линейного однородного уравнения.
Составить это уравнение.
Решение:
1). Имея решение
уравнения:
,
учтем: 1 =
→
=0.
2). Учитывают, что
если решения уравнения:
и
,
то их «порождают» характеристические
корни уравнения:
.
У нас:
,
.
3). Имея корни
,
восстановим характеристический
многочлен:
=
.
4). Имея
характеристический многочлен, восстановим
ДУ:
Ответ: уравнение:
.
Пример 8–12:
По
данным корням:
=
=1
характеристического уравнения ЛОУ с
постоянными коэффициентами составить
ДУ и написать его общее решение.
Решение:
1). Учтем стандартную
запись уравнения 2-го порядка:
.
2). В нашем случае
получим:
.
3). По заданным
корням составляем ФСР:
,
и общее решение:
.
Ответ: уравнение:
.
ФСР:
,
.Общее решение:
.
Пример 8–13:
Найти
общее решение ДУ:
.
Решение:
1). Составим
характеристическое уравнение:
,
его корни:
=
.
2). Составляем ФСР:
,
и общее решение:
.
Ответ: ФСР:
,
.Общее решение:
.
Пример 8–14:
Найти
общее решение ДУ:
.
Решение:
1). Составим
характеристическое уравнение:
,
его корни:
=–
,
=2.
2). Составляем ФСР:
,
и общее решение:
.
Ответ: ФСР:
,
.Общее решение:
.
Пример 8–15:
Найти
частное решение ДУ:
,
,
.
Решение:
1). Составим
характеристическое уравнение:
,
его корни:
=1
– кратный.
2). Составляем ФСР:
,
и общее решение:
=
.
Найдем производную:
.
3). Для заданных
начальных условий:
=
,
=
.
Находим:
,
.
Следует частное решение:
.
Ответ: частное
решение:
.
☻
Вопросы для самопроверки:
Задано уравнение 2-го порядка. Как проверить, что функция
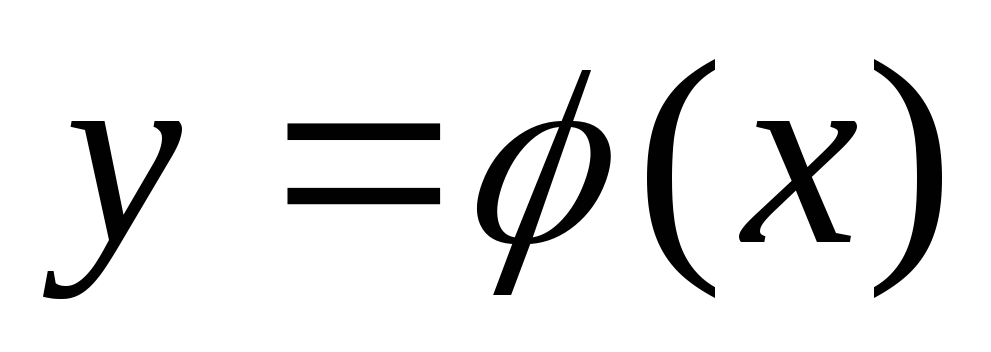есть решение уравнения?Задано семейство кривых. Как найти уравнение, для которого семейство есть решение?
Имеем совокупность функций. Что значит: функции линейно зависимы?
Что такое «определитель Вронского»?
Как определить, зависимы или нет функции данной совокупности?
Что такое «фундаментальная система решений – ФСР»?
Может ли понятие ФСР применяться к неоднородным уравнениям?
Как записывают общее решение линейного однородного дифференциального уравнения?
Каковы свойства общего решения ДУ?
Что значит решить задачу Коши для ДУ второго порядка?
Какова роль определителя Вронского при решении задачи Коши для ДУ n-го порядка?
• ◄ ≡ ► •