3.1. Определитель Вронского.

Пусть имеем совокупность функций: ,,...,и необходимо установить, зависима или нет эта совокупность. Оказывается, использование определителя Вронского позволяет решить вопрос о линейной зависимости (и независимости) совокупности функций.

Теорема: (8.4)

Если функции ,,..., линейно зависимы на интервале , и имеют производные до - го порядка, то определитель (Вронского): = тождественно равен нулю для всех .

►Доказательство теоремы:

Запишем функцию: =. Так как по условию функции ,,..., линейно зависимы на , то существуют такие числа , не все равные нулю, что выполняются тождество: 0 для всех . Дифференцируя раз функцию , получим тождества 0,0,..., 0, которые также выполняются для всех . Полученные тождества эквивалентны системе линейных однородных уравнений:

0,

0,

. . . . . . . . . . . . . , (13)

0.

В соответствии с определением линейной зависимости функций ,,..., система уравнений (13) должна иметь ненулевое решение для любого . Но это возможно только в случае, если определитель этой системы равен нулю (вспомним теорему Кронекера-Капелли!), причём для всех . Нетрудно заметить, что определитель системы (13) есть определитель Вронского . Это значит, что теорема доказана! ◄

Следствие: Если хотя бы в одной точке , то функции ,,..., – линейно независимы на интервале .

Итак, определитель Вронского позволяет установить свойство для совокупности функций,,...,, которые являютсяфункциями-решенияминекоторого линейного однородного дифференциального уравнения- го порядка.

Более того, используя результаты теории линейных векторных пространств (вспомним курс Линейная алгебра!), можем установить, что совокупность функций-векторов ,,...,естьбазис в пространстве решенийлинейного дифференциального уравнения- го порядка. Но, тогдалюбое решениетакого уравнения может быть записано в виде линейной комбинации:=. Это значит, что свойствомы также доказали.

Остаётся доказать свойство ФСР, но, прежде познакомимся поближе с определителем Вронского, рассмотрев несколько Примеров.

☺☺

Пример 8–02: Исследовать на линейную зависимость систему функций: ,,.

Решение:

1). Для исследования линейной зависимости совокупности функций ,, составим линейную комбинацию заданных функций: .

2). Так как , то при любом значении указанное равенство выполняется. Это значит, что совокупность функций зависима.

Ответ: совокупность функций зависима.

Замечание: В рассмотренном примере не потребовалось вычислять определитель Вронского, но мы знаем, что в этом случае он равен нулю, так как установлена линейная зависимость совокупности функций.

Пример 8–03: Исследовать на линейную зависимость систему функций: ,.

Решение:

1). Нетрудно заметить, что . Но, тогда . Согласно второму определению линейной зависимости совокупности функций, можем утверждать, что совокупность функций , зависима.

2). И в этом примере определитель Вронского равен нулю, хотя вычислять его не пришлось.

Ответ: совокупность функций зависима.

Замечание: В рассмотренных примерах не потребовалось вычислять определитель Вронского, но мы знаем, что в этом случае он равен нулю, так как установлена линейная зависимость совокупности функций.

Пример 8–04: Задана совокупность функций: ,, . Исследовать линейную зависимость этой совокупности.

Решение:

1). Для решения вопроса о независимости системы функций построим определитель Вронского:

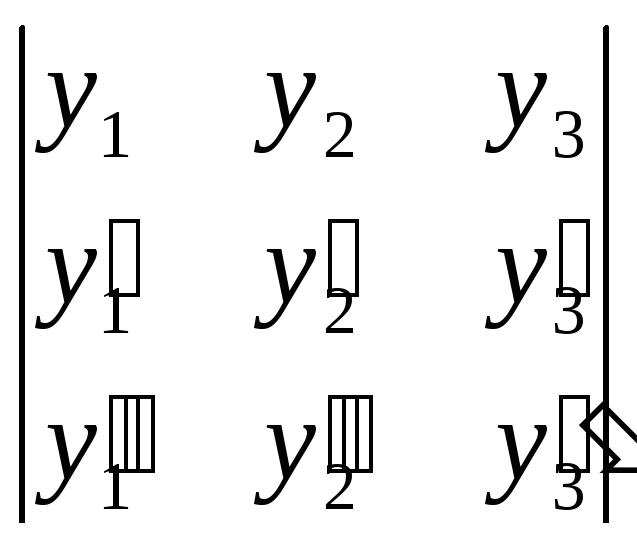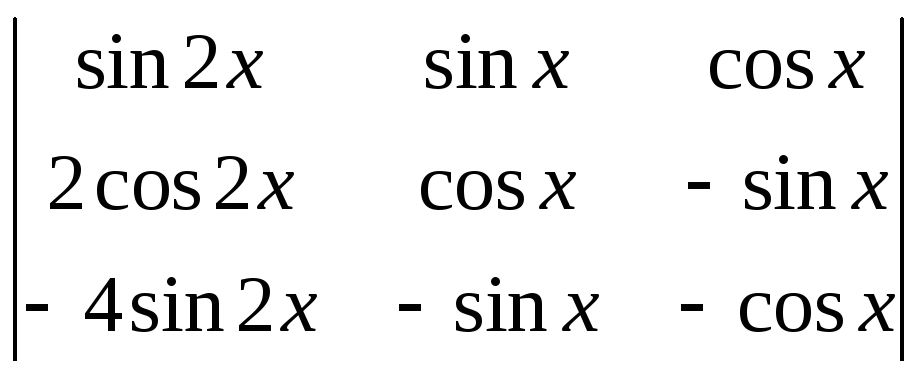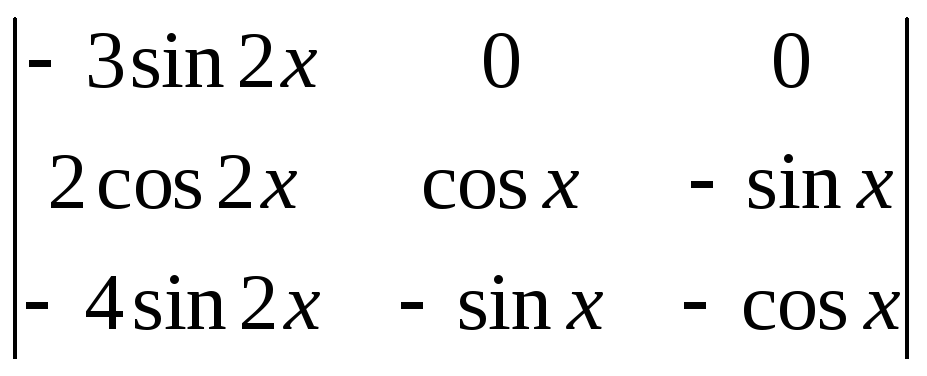=== 3.

2). Видим: определитель Вронского не равен (тождественно) нулю. Это значит, что заданная совокупность функций линейно независима.

Ответ: совокупность функций независима.

☻

В Теореме 8.4 рассмотрена произвольная совокупность функций. А что, если совокупность функций ,,...,составлена из решений линейного однородного уравнения? Оказывается верна следующая Теорема.

Теорема: (8.5)

Для того, чтобы решения линейного однородного дифференциального уравнения: , (14) с непрерывными коэффициентами , были линейно независимы на интервале , необходимо и достаточно, чтобы определитель для всех .

►Доказательство теоремы:

1). Пусть для всех . В таком случае функции ,,..., линейно независимы на интервале , в любом случае: будут эти функции решениями уравнения (14), или нет.

2). Пусть теперь имеем решения ,,..., уравнения (14), причем известно, что они линейно независимы на . Допустим, что все-таки нашлось значение = такое, что =0. Составим систему уравнений (формально):

=0,

=0,

. . . . . . . . . . . . . . . . . . . . . , (15)

=0.

Система (15) есть система линейных однородных уравнений. По предположению =0, следовательно, для точки = она имеет ненулевое решение.

Обозначим строки системы уравнений (15) через: =0, =0, ... , =0. Теперь учтем, что линейная комбинация = есть тоже решение уравнения (14): в соответствии с доказанными Теоремами 8.2 и 8.3. Примем для функции в качестве начальных условий: =0, =0, ... , =0.

Но для уравнения (14) решением будет и такая функция: 0 (очевидно!), причем с начальными условиями: y(x₀)=0, y′(x₀)=0, ... , y^(n–1)(x₀)=0. Так как для уравнения (14) выполняются условия Теоремы о существовании и единственности решений (для нас сейчас важно второе!), то функции = и y ≡ 0 должны совпадать для всех . Но это значит, что решения ,,..., – линейно зависимы. Противоречие!..

Итак, если решения уравнения (14) линейно независимы, то определитель не может быть равным нулю ни в одной точке области определения: . ◄

☺☺

Пример 8–05: Задана совокупность функций: ,, . Исследовать линейную зависимость этой совокупности.

Решение:

1). Для решения вопроса о независимости системы функций построим определитель Вронского:

==.

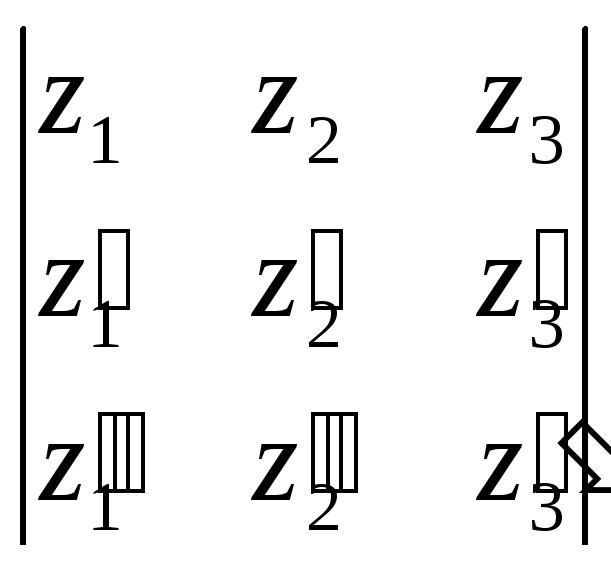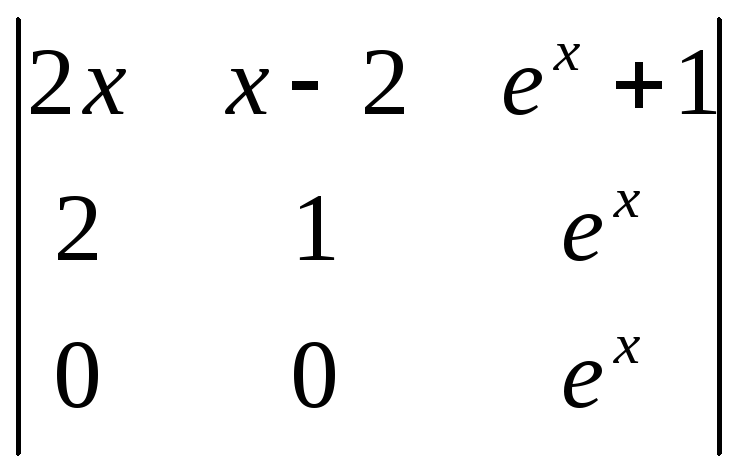2). Видим: определитель Вронского не равен нулю. Это значит, что заданная совокупность функций линейно независима для любых значений .

Ответ: совокупность функций независима для любых значений .

☻
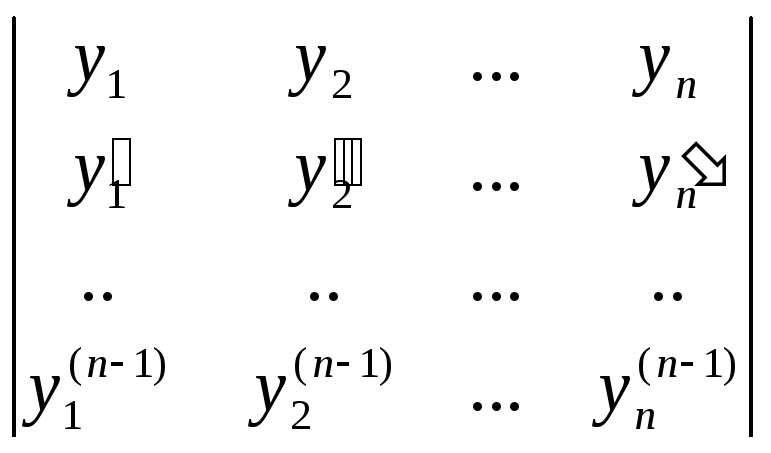