1 семестр / Линейная Алгебра / Новая папка / ржавинская лекции / Лекция_7

Лекция 7

Обратная матрица. Ранг матрицы

Построение обратной матрицы методом присоединенной. Ранг матрицы. Нахождение ранга матрицы методами окаймляющих миноров и элементарных преобразований

7.1. Обратная матрица

Далее будут рассматриваться квадратные матрицы.

Единичная матрица

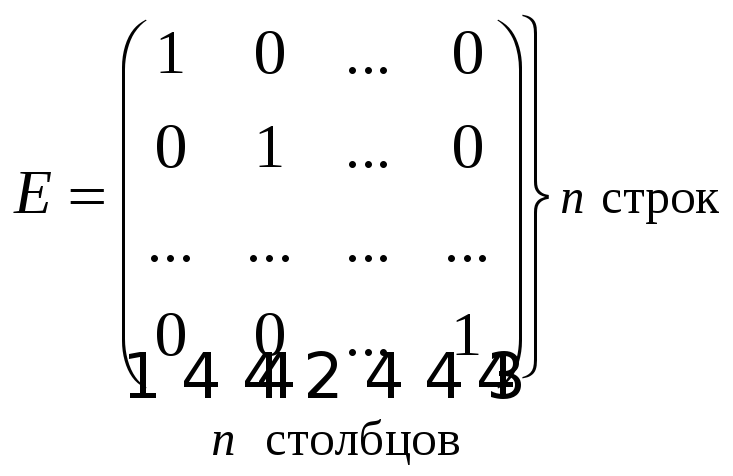
в умножении квадратных матриц порядка играет роль, аналогичную роли числа единица в умножении чисел:

. (7.1)

Действительно, пусть

.

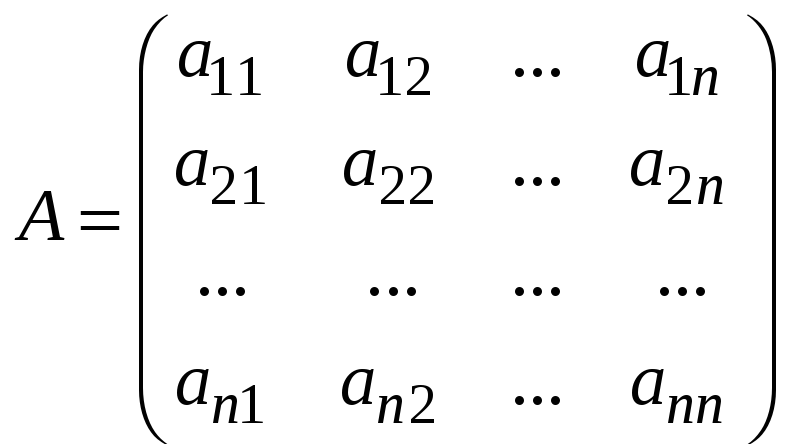Непосредственная проверка дает: . Аналогично , и равенство (7.1) справедливо.

Утверждение 1. Матрица - единственная матрица, обладающая свойством (7.1).

Доказательство. Пусть такая, что

. (7.2)

Рассмотрим произведение :

.

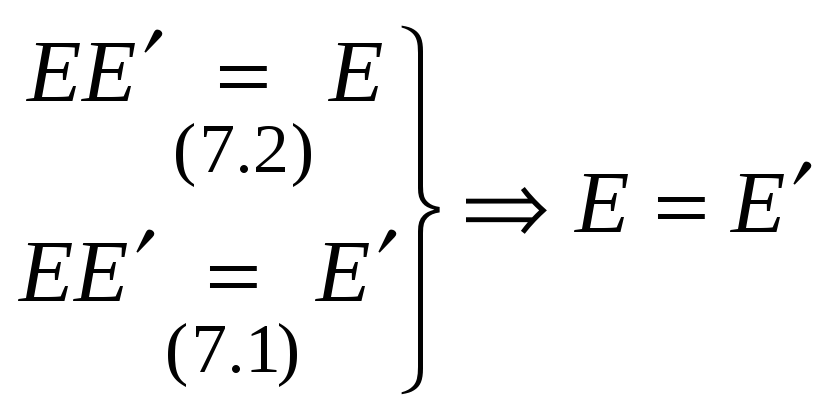Определение 1. Пусть - произвольная квадратная матрица. Матрица называется правой обратной для , если . Матрица называется левой обратной для , если .

Определение 2. Квадратная матрица называется вырожденной (особенной), если , и невырожденной (неособенной), если .

Утверждение 2. Вырожденная матрица не имеет ни правой, ни левой обратной.

Доказательство. Пусть - вырожденная. Допустим, - правая обратная для , т.е. .

Тогда , но , что является противоречием, следовательно, не имеет правой обратной.

Аналогично доказывается, что не имеет и левой обратной.

Утверждение 3. Пусть - произвольный определитель порядка . Сумма произведений всех элементов любого столбца (строки) на алгебраические дополнения соответствующих элементов другого столбца (строки) равна нулю.

Доказательство. Пусть

.

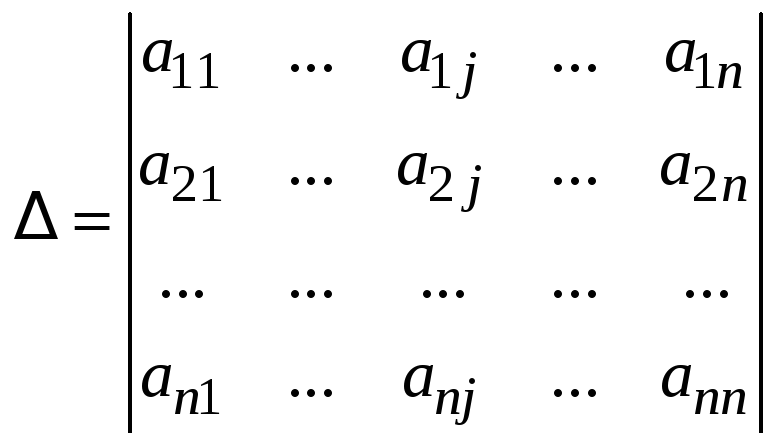В силу теоремы о разложении по строке (лекция 6, теорема 1) имеем

,

где - алгебраическое дополнение к элементу .

Пусть - произвольные вещественные числа. Рассмотрим сумму .

Привлекая ту же теорему о разложении по строке, можем записать

.

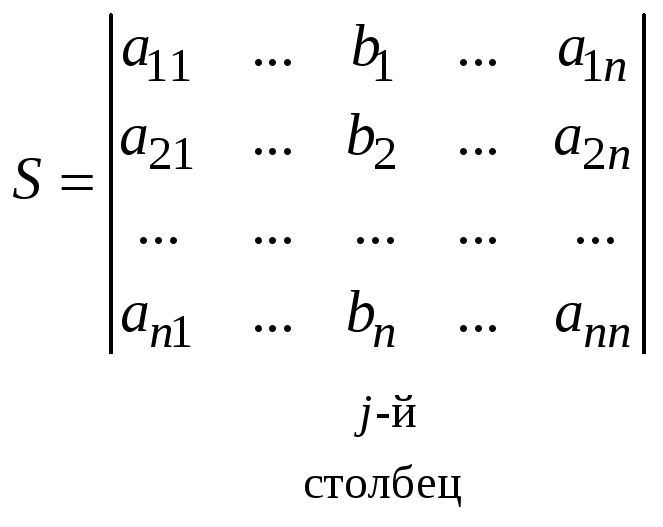Возьмем в качестве чисел , , элементы -го столбца определителя , , тогда

Утверждение 3 доказано.

Перейдем к построению обратной матрицы методом присоединенной. Пусть - невырожденная матрица порядка :

.

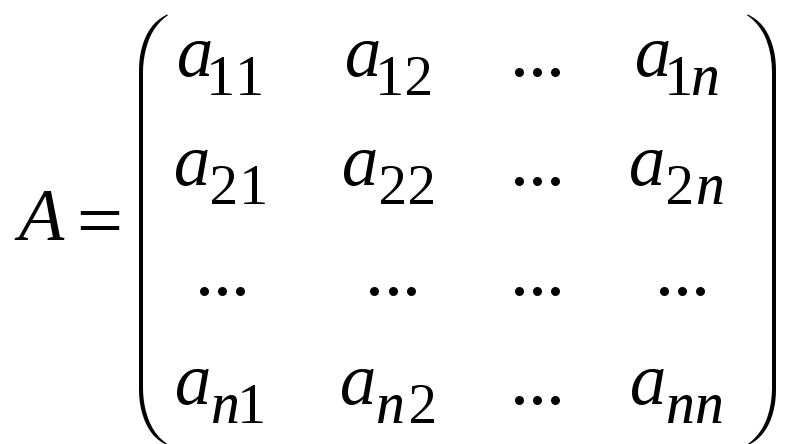Матрица

называется присоединенной для . Элементами матрицы являются алгебраические дополнения к элементам матрицы , причем алгебраические дополнения к элементам i-й строки матрицы помещены в i-й столбец .

Обозначим .

Матрица является правой и левой обратной для .

Действительно,

Следовательно, матрица - правая обратная для . Аналогично , и матрица является и левой обратной для . Она называется обратной для и обозначается .

Итак,

.

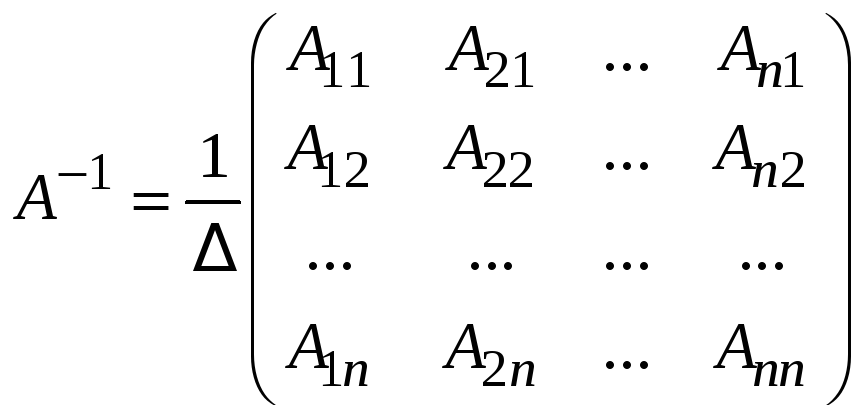Утверждение 4. Матрица - единственная обратная для .

Действительно, допустим, такая, что .

Рассмотрим . С другой стороны, , следовательно, .

Пример 1. Найти для матрицы .

Решение. Имеем , следовательно, существует.

Найдем алгебраические дополнения к элементам матрицы и составим присоединенную матрицу:

.

Откуда .

Пример 2. Решить матричное уравнение

.

Решение. Обозначим . Тогда исходное уравнение примет вид

. (7.3)

Имеем

.

Домножим обе части уравнения (7.3) слева на матрицу и получим

.

Итак,

,

.

Упражнения. Доказать следующие свойства обратной матрицы.

1. Если , то .

2. .

3. .

7.2. Ранг матрицы

Пусть - прямоугольная матрица размера :

.

Назовем арифметическими -мерными векторами упорядоченные наборы чисел, строки матрицы , и обозначим их через , ,…,.

Нулевым арифметическим вектором назовем .

Будем говорить, что система векторов линейно зависима, если , не все равные нулю, что .

Система векторов называется линейно независимой, если она не является линейно зависимой.

Пример 3. В матрице

, , .

Имеем , следовательно, и система строк матрицы линейно зависима.

Заметим, что и столбцы матрицы можно рассматривать как арифметические -мерные векторы.

Определение 3. Пусть - прямоугольная матрица размера . Выберем в произвольные строк и столбцов. Элементы, стоящие на пересечении выбранных строк и столбцов, образуют определитель порядка , который называется минором порядка матрицы .

Определение 4. Наивысший порядок отличных от нуля миноров матрицы называется рангом матрицы .

Обозначение ранга : .

Пример 4. Найти ранг матрицы :

.

Решение. Заметим, что миноры первого порядка - это элементы матрицы. Выпишем их все (в данном случае, миноров первого порядка восемь): .

Уже на этом шаге можно утверждать, что , так как среди миноров 1-го порядка есть отличные от нуля.

Выпишем все миноры 2-го порядка:

, , , , ,

и отметим, что, например, и по определению 4 (миноров третьего порядка из элементов матрицы составить нельзя, так как содержит всего две строки).

Пусть матрица имеет размер и . Это означает, что хотя бы один минор порядка отличен от нуля, а все миноры порядка и выше равны нулю. Минор называется базисным, а столбцы матрицы, его содержащие, - базисными столбцами матрицы (строки, содержащие минор , называются базисными строками).

Теорема 1 (о базисном миноре). Столбцы, содержащие базисный минор, линейно независимы. Любой столбец матрицы является линейной комбинацией базисных столбцов одного и того же базисного минора.

Доказательство. Пусть и отличен от нуля минор , расположенный в первых строках и первых столбцах матрицы , т.е. в левом верхнем углу:

.

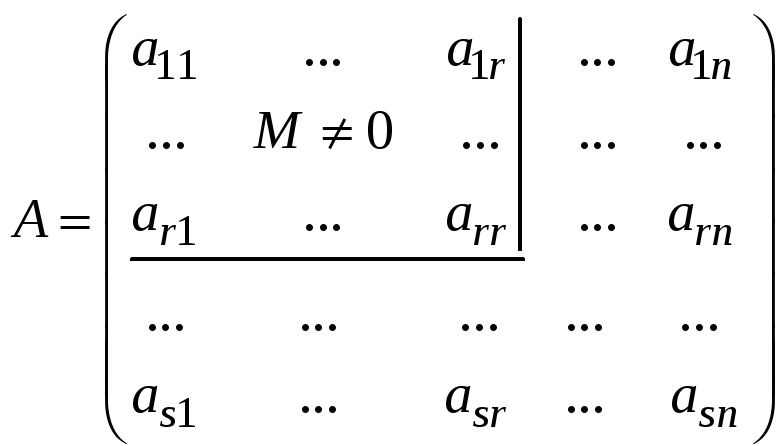Докажем сначала, что арифметические векторы

, ,

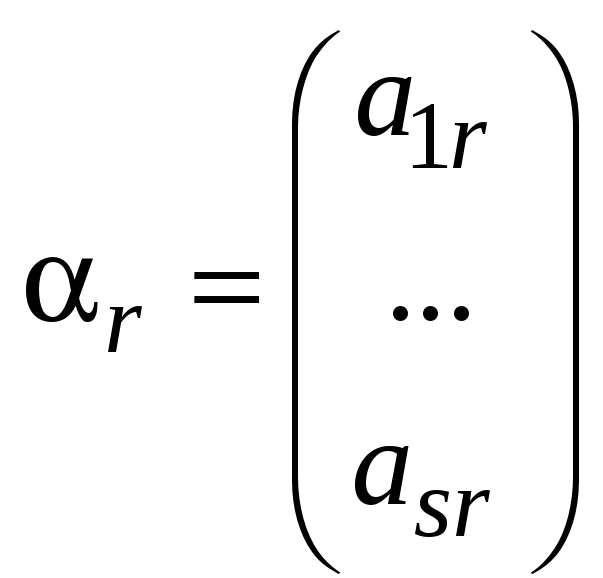
составляют линейно независимую систему.

Допустим, что линейно зависимы, тогда , , что , т.е. выполняется система тождеств:

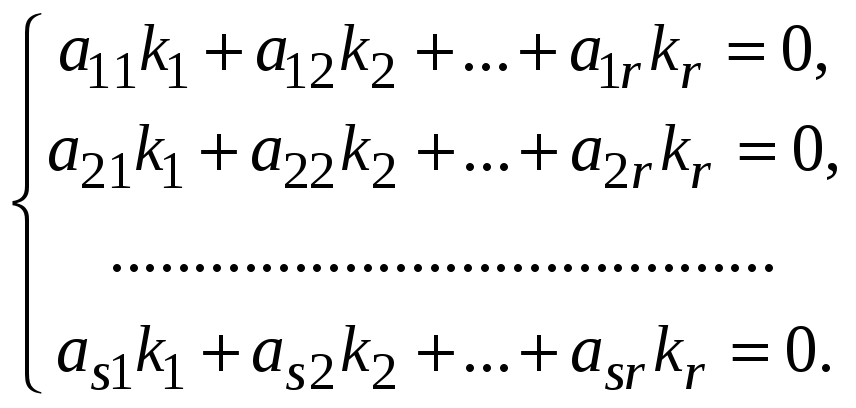(7.4)

Первые равенств системы (7.4) можно переписать в виде

.

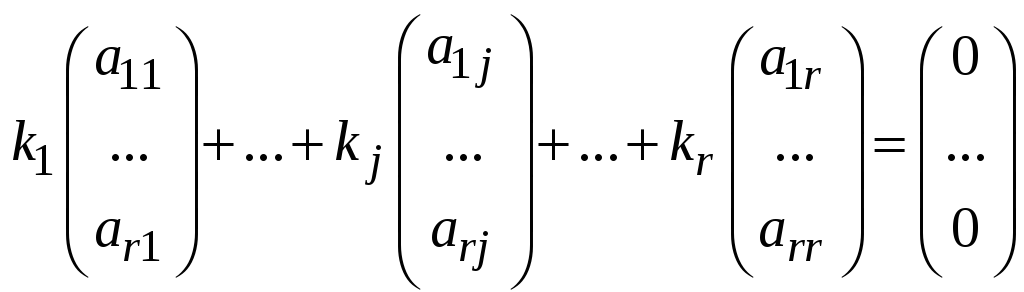Учитывая, что , получим

;

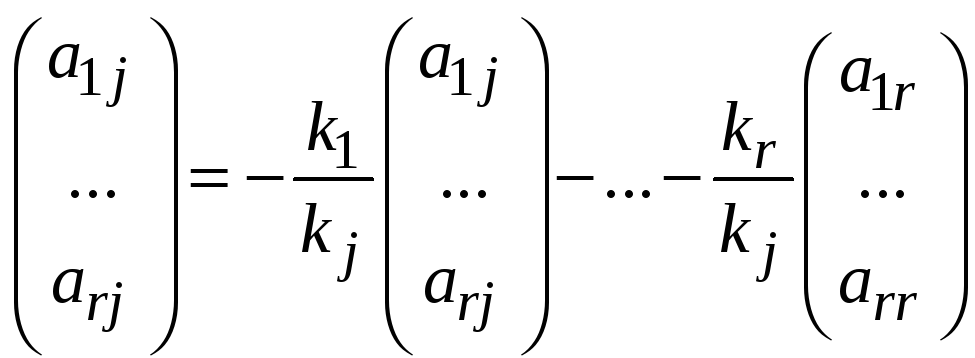-й столбец определителя оказался линейной комбинацией остальных. Тогда - противоречие, и, следовательно, векторы линейно независимы.

Докажем теперь, что любой столбец матрицы является линейной комбинацией первых столбцов.

Рассмотрим вспомогательный определитель

,

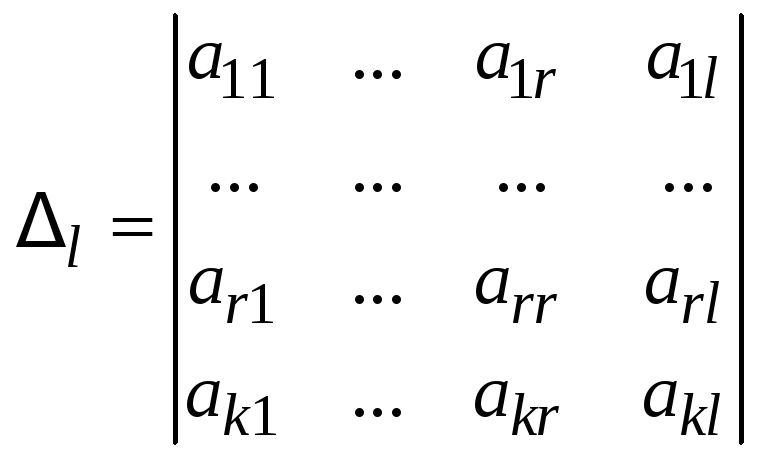полученный "окаймлением" минора элементами -й строки и -го столбца, . Утверждается, что .

Действительно, возможны два случая.

Случай 1: . Тогда - минор матрицы порядка и по условию (наивысший порядок отличных от нуля миноров равен , следовательно, все миноры порядка равны нулю).

Случай 2: . Тогда содержит две одинаковые строки, следовательно, .

Итак, всегда . Разложим по последней строке.

Отметим, что если - алгебраическое дополнение к элементу из последней строки определителя , то

,

и не зависит от ( был номером строки в матрице , а в эти элементы занимают -ю строку). Поэтому алгебраические дополнения к элементам в , , можем обозначить .

.

Полагая , получим равенств:

,

,

…………………………………………

,

или в матричной форме:

,

т.е. -й столбец матрицы оказался линейной комбинацией первых столбцов с коэффициентами .

Было принято, что .

Если , то

.

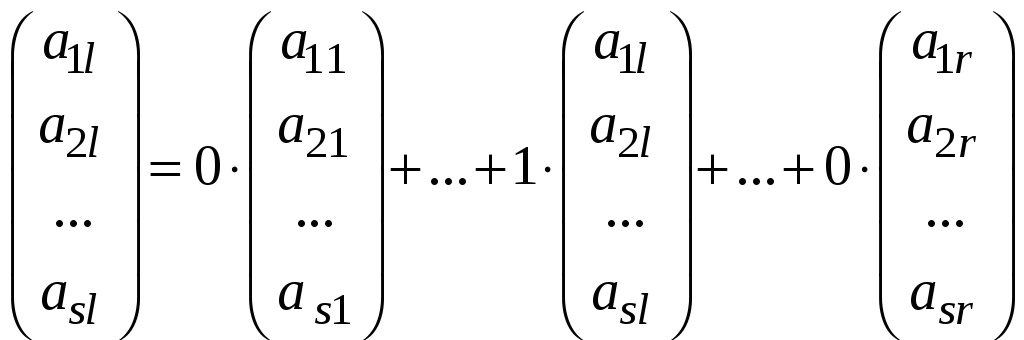Таким образом, любой столбец матрицы является линейной комбинацией базисных столбцов.

Теорема доказана.

Замечание. Аналогичное утверждение справедливо и для строк: строки, содержащие базисный минор, линейно независимы, через них линейно выражаются все остальные строки матрицы.

Теорема 2. Если в матрице некоторый минор порядка отличен от нуля, а все окаймляющие его миноры равны нулю, то .

Доказательство этого утверждения опустим.

Пример 5. Найти ранг матрицы :

Решение. Имеем (следовательно, ).

; ();

;

;

.

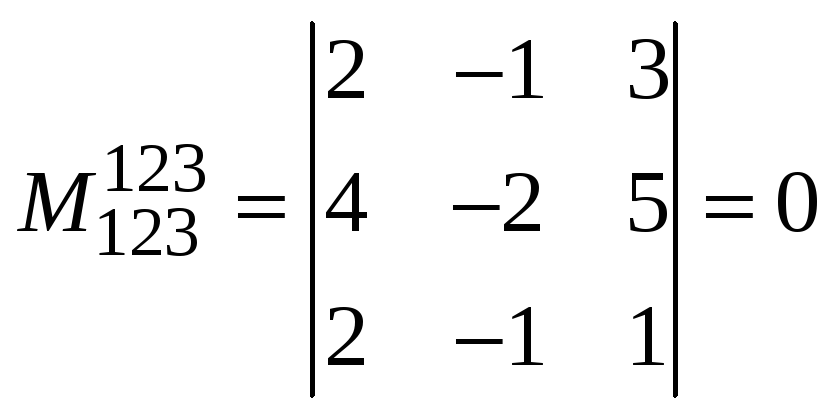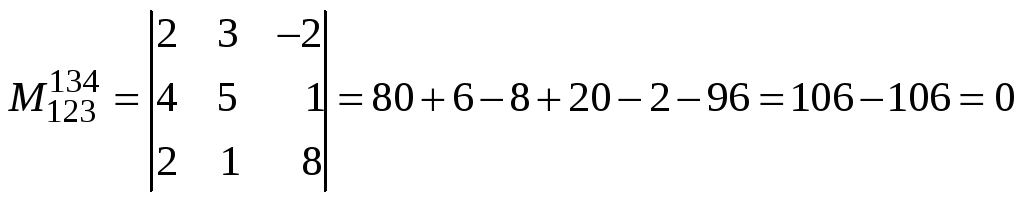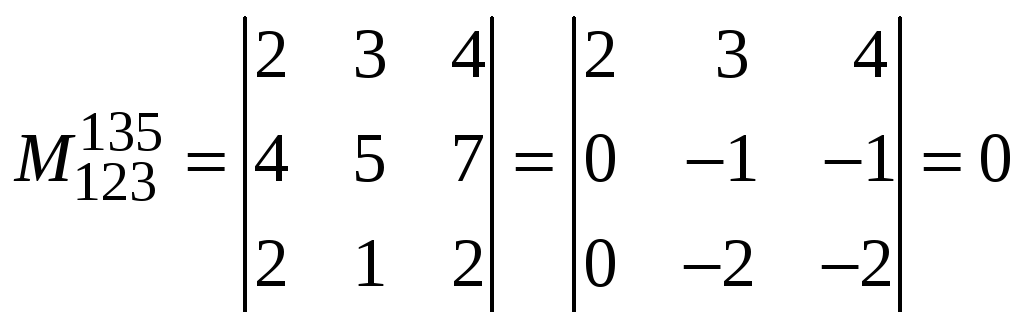Таким образом, известен минор второго порядка, отличный от нуля (), а все миноры третьего порядка, окаймляющие его, равны нулю, следовательно, .

Базисный минор . Через первый и третий столбцы линейно выражаются остальные столбцы матрицы.

Изложенный способ нахождения ранга матрицы называется методом окаймляющих миноров.

Метод элементарных преобразований

Определение 5. Элементарными преобразованиями матрицы называются следующие:

1) перестановка двух строк (столбцов) матрицы;

2) умножение всех элементов строки (столбца) на вещественное число ;

3) прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), умноженных на одно и то же число.

Справедливо следующее утверждение, которое приводится без доказательства.

Теорема 3. Элементарные преобразования не изменяют ранга матрицы.

Определение 6. Матрица размером имеет диагональную форму, если , кроме , , т.е.

.

Отметим, что , так как минор порядка , расположенный в левом верхнем углу (в первых строках и первых столбцах), отличен от нуля, а все миноры, окаймляющие его, равны нулю (они содержат столбец из нулей).

Утверждение. Всякую матрицу элементарными преобразованиями можно привести к диагональной форме.

Действительно, пусть

.

Если , то по определению 6 имеет диагональную форму.