6.3. Основные операции над матрицами
Определение 5. Две матрицы
,
,
,
и
,
,
,
будем называть равными, если
.
Краткая запись:
.
Таким образом, две матрицы считаются равными, если они имеют одинаковые порядки и их соответствующие элементы равны.
Определение 6. Суммой двух матриц
,
,
,
и
,
,
,
называется такая матрица
,
,
,
что
.
Иначе говоря, складывать можно только матрицы одних и тех же порядков, причем сложение осуществляется поэлементно.
Пример 8. Найти сумму матриц
и
.
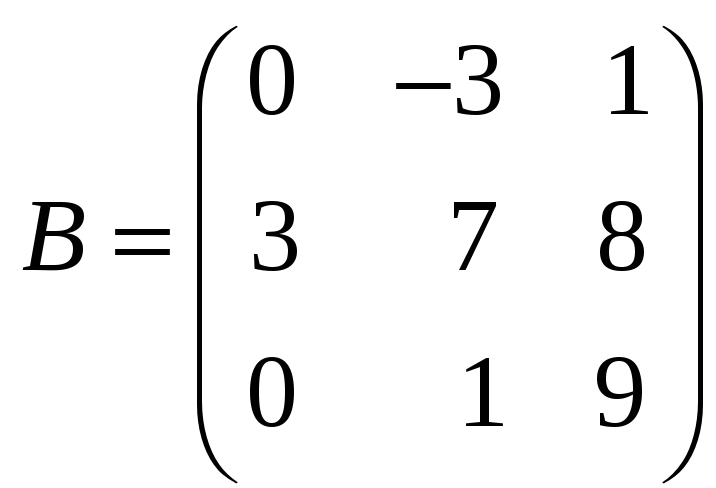В соответствии с определением 6 найдем
.
Правило сложения матриц распространяется на сумму любого конечного числа слагаемых.
Определение 7. Произведением
матрицы
,
,
,
на вещественное число
называется такая матрица
,
,
,
для которой
.
Иными словами, чтобы умножить матрицу на число, нужно умножить на это число все ее элементы и оставить полученные произведения на прежних местах.
Пример 9.
Найти линейную комбинацию
матриц
и
.
Пользуясь определением 7, получаем
,
,
далее привлекаем определение суммы матриц (определение 6):
.
Свойства операций сложения матриц и умножения на число:
1. Сложение коммутативно:
.
2. Сложение ассоциативно:
.
3. Существует нулевая матрица
,
удовлетворяющая условию
для всех А.
4. Для любой матрицы А существует
противоположная матрица В,
удовлетворяющая условию
.
Для любых матриц А и В и любых
действительных чисел
имеют место равенства:
5.
.
6.
.
7.
.
8.
.
Проверим свойство 1. Обозначим
,
.
Пусть
,
,
.
Имеем
,
и так как равенство доказано для
произвольного элемента, в соответствии
с определением 5
.
Свойство 1 доказано.
Аналогично доказывается свойство 2.
В качестве матрицы
возьмем матрицу порядка
,
все элементы которой равны нулю.
Сложив
с любой матрицей
по правилу, данному в определении 6, мы
матрицу
не изменим, и свойство 3 справедливо.
Проверим свойство 4. Пусть
.
Положим
.
Тогда
,
следовательно, свойство 4 справедливо.
Проверку свойств 5 - 8 опустим.
Определение 8. Произведением
матрицы
,
,
,
на матрицу
,
,
,
называется матрица
,
,
,
с элементами
.
Краткая запись:
.
Пример 10. Найти произведение матриц
и
.
В соответствии с определением 8 найдем
.
Пример 11. Перемножить матрицы
и
.
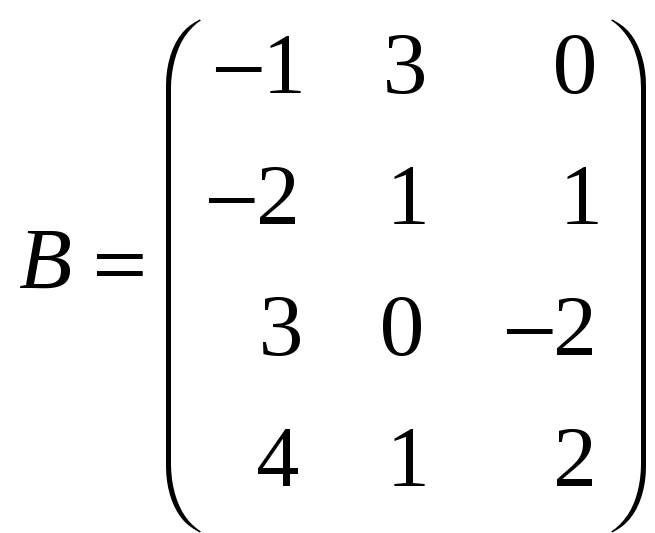Имеем
.
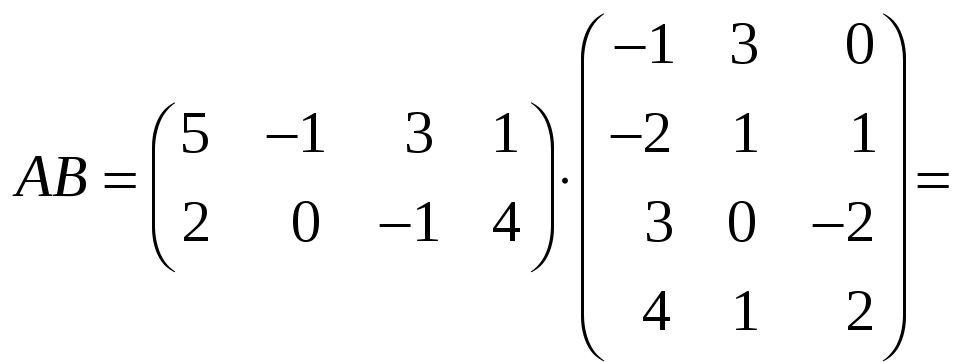
Замечание 1.
Число элементов в строке матрицы
равно числу элементов в столбце матрицы
(число столбцов матрицы
равно числу строк матрицы
).
Замечание 2.
В матрице
строк столько же, сколько в матрице
,
а столбцов столько же, сколько в
.
Замечание 3.
Вообще говоря,
(умножение матриц некоммутативно).
Чтобы обосновать замечание 3, достаточно привести хотя бы один пример.
Пример 12.
Перемножим в обратном порядке матрицы
и
из примера 10.
,
таким образом, в общем случае
.
Отметим, что в частном случае равенство
возможно.
Матрицы
и
,
для которых выполняется равенство
,
называются перестановочными, или
коммутирующими.
Упражнения.
1. Найти все матрицы, перестановочные с данной:
а)
;
б)
.
2. Найти все матрицы второго порядка, квадраты которых равны нулевой матрице.
3. Доказать, что
.