|
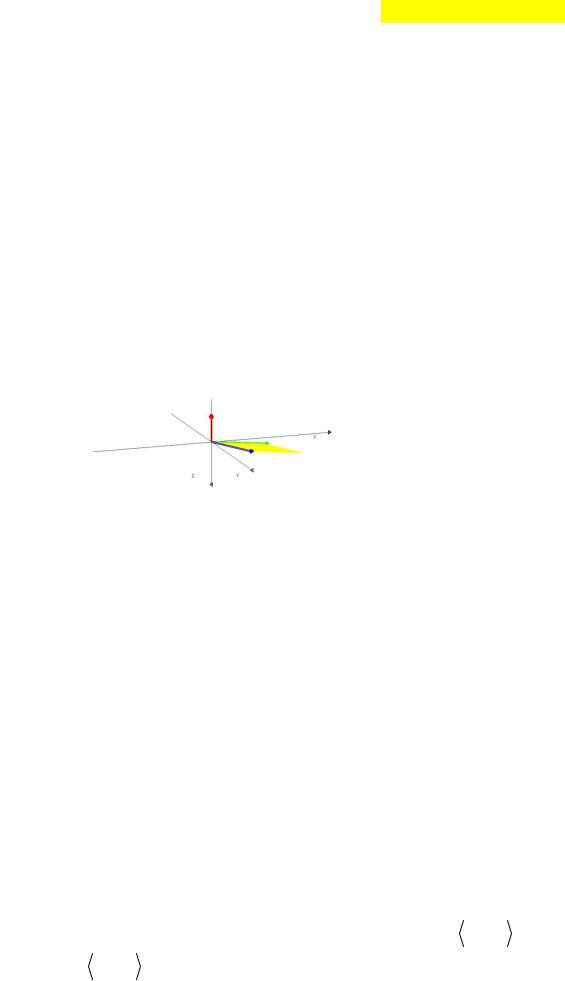
образуют правую тройку. 1,2,0 |
, |
зеленый вектор |
b |
2,1,0 |
и красный вектор |
c |
a b |
|||||||
Выводы: Синий вектор |
|
|
|
|
|
|
|
||||||||
0,0, 3 |
|
Вектор |
c |
перпендикулярен |
плоскости векторов |
|
и |
b |
. |
|
|
||||
|
|
|
|
|
|
|
|||||||||
С длиной вектора дело обстоит сложнее. |
|
|
|
|
|
|
|
|
|
|
|||||
Найдем длину вектора . В данном случае очевидно, что длина вектора равна 3. |
|
|
|
||||||||||||
Изобразим параллелограммc |
, натянутый на векторы |
и . |
|
|
|
|
|
|
|
||||||
Еще раз напишем, что |
|
|
|
|
|
b |
S |a||b|sin a,b |
3 |
|||||||
длина вектора c равна площади желтого параллелограмма |c | |
|||||||||||||||
Изобразим плоскость желтого параллелограмма:
>>x1=0:0.1:1.9;y1=0:0.05:0.95;x2=1:0.1:2.9;y2=2:0.05:2.95;
>>line([x1; x2],[y1; y2],'Color','yellow','LineWit')
Изучите внимательно как здесь мы работаем с функцией line.
Далее можно повозиться с рисунком с помощью инструментов графического окна. Здесь рисунок повернут так, чтобы красный вектор c смотрел вверх. На этом рисунке еще более очевидно, что синий, зеленый и красный векторы образуют правую тройку.
---------------------------------------------------------------Упр. 3.16.(конец)
Таким образом, для решения и исследования других подобных задач, можно договориться, что первый вектор правой тройки мы рисуем синим цветом, второй - зеленым, а третий - красным цветом.
Упражнение 3.17.
Вычислить площадь треугольника с вершинами A = (1; 3; −1), B = (2; −1; 4) и
C = (5; 0; 3). Изобразить плоскость треугольника. Как соотносятся площадь треугольника и
векторное произведение. Изобразить это соответствие по аналогии с предыдущим упражнением.
Смешанное произведение |
|
|
|
||
|
|
|
r r |
r r r |
r r |
Смешанным произведением векторов a,b,c (обозначается: |
a,b,c |
или a b c ) |
|||
r r r |
r r |
r |
(10) |
|
|
называется число a,b,c |
= a, b |
c. |
|
|
|
|
|
|
|
|
|
31 |
|
|
|
|
|
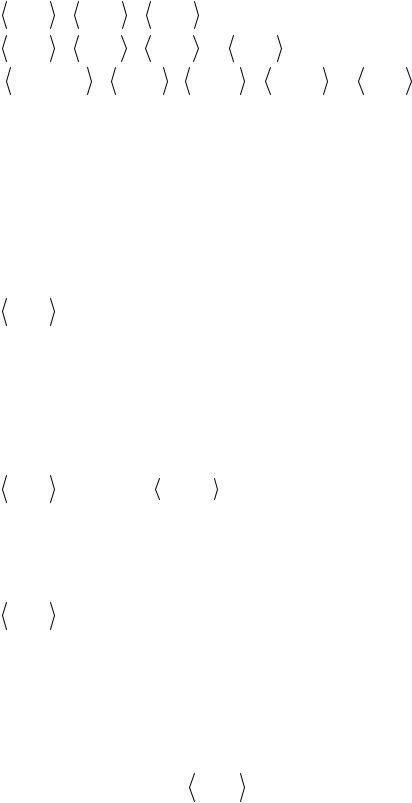
Свойства смешанного произведения: |
|
|
|
|
|
||||||||||
r r r |
= |
r |
r |
r |
= |
r r r |
|
|
|
(11) |
|
|
|
||
a,b,c |
b,c, a |
c, a,b |
; |
|
|
|
|
|
|
||||||
r r r |
= |
r |
r |
r |
= |
r r r |
= − |
r |
r |
r |
|
|
|
(12) |
|
b, a,c |
c,b, a |
a,c,b |
a,b,c ; |
|
|
|
|
||||||||
r r′ |
r |
r |
= |
r |
r |
r |
r′ r |
r |
; |
r r |
= λ |
r |
r |
r |
(13) |
a + a , b, c |
a, b, c + |
a , b, c |
λa,b,c |
a,b,c . |
|||||||||||
Свойства (11) и (12) означают, что смешанное произведение не изменяется при круговых перестановках аргументов и умножается на −1 при других перестановках. Свойства (13) выражают линейность смешанного произведения векторов по первому аргументу. Имеет место также линейность по второму и третьему аргументу.
Геометрический смысл смешанного произведения |
|
|
r |
|
|
|||||||||||||||
Пусть V =Var,br,cr |
|
|
|
|
|
|
|
|
|
|
r |
r |
|
|||||||
– объём параллелепипеда, построенного на векторах a,b,c (считается, |
||||||||||||||||||||
что Var,br,cr = 0, |
если ar, br, cr |
компланарны). Тогда |
|
|
|
|
|
|||||||||||||
r |
r |
r |
|
|
|
|
|
|
|
r |
r r |
− правая тройка, |
|
|
|
|
|
|||
|
+V , если a, b, c |
(14) |
|
|
|
|
||||||||||||||
a,b,c |
= |
|
|
|
|
|
|
|
r r |
− левая тройка. |
|
|
|
|
||||||
|
|
|
−V , если ar, b, c |
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Выражение смешанного произведения |
|
|
|
|
|
|||||||||||||||
через координаты векторов |
|
|
|
|
|
|
||||||||||||||
Пусть er1, er2 , er3 |
– базисные векторы некоторой системы координат Oxyz (вообще говоря, |
|||||||||||||||||||
косоугольной). Если ar = a1er1 +a2er2 +a3er3 , |
b = b1er1 +b2er2 +b3er3 , c = c1er1 +c2er2 +c3er3 , то |
|
||||||||||||||||||
r |
r |
r |
= |
|
a1 a2 a3 |
|
|
|
r r r |
(15) |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|||||||||||||
a,b,c |
|
b1 |
b2 |
b3 |
|
|
e1,e2 |
,e3 . |
|
|
|
|
|
|||||||
|
|
|
|
|
c1 |
c2 |
c3 |
|
|
|
|
|
|
r |
r |
r |
r |
r |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Если же система координат прямоугольная и базисные векторы i |
= e1, |
j |
= e2 , |
k = e3 |
||||||||||||||||
образуют правую тройку, то |
|
|
|
|
|
|
|
|||||||||||||
r |
r |
r |
|
|
a1 |
a2 |
a3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
= |
|
b1 |
b2 |
b3 |
|
|
. |
|
|
(16) |
|
|
|
|
|
|||||
a,b,c |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
c1 |
c2 |
c3 |
|
|
|
|
|
|
|
|
|
|
|||
Замечание. Формула (15) верна и в случае, если векторы e1, er2 , er3 не образуют базиса (но векторы ar,br,cr выражены через них) – в этом случае левая и правая части равенства (15) равны 0.
Условие компланарности векторов |
|
|||
r r r |
|
r r r |
= 0. |
(17) |
a,b,c компланарны |
a, b, c |
|||
32
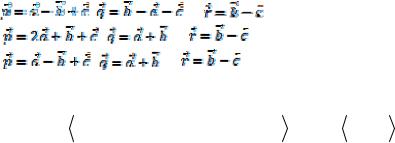
Упражнение 3.19.
Найти смешанное произведение векторов ar,b,cr, где векторы b и c перемножаются векторно, а
их результат на вектор скалярно, см формулу (10). Затем найти смешанное произведение по формуле (16).
Проверить свойства (11) и (12) смешанного произведения по формуле (10). |
|
|
|
||
Упражнение 3.19. |
|
|
|
|
|
С помощью смешанного произведения доказать, что векторы |
|
, |
|
и |
|
1,2,2 |
компланарны, определить ориентацию этой тройки. Ответьте |
на вопрос: как это связано |
|||
|
1, 2,0 |
|
0,1,1 |
|
|
понятие компланарность с понятиями базис и линейная зависимость для этих векторов. Построить эти векторы. Вектор изобразить синим, вектор зеленым, вектор красным.
Упражнение 3.20
Исследовать с помощью смешанного произведения векторы
на компланарность ,
векторы ar,br,cr-некомпланарны, их смешанное произведение равно +1.
A) |
|
|
|
|
, |
|
|
|
|
и |
|
|
, |
|
|
|
|
B) |
|
|
|
|
|
, |
|
|
и |
|
|
, |
|
|
|
|
|
C) |
|
|
|
|
, |
|
|
|
и |
|
|
. |
|
|
|
|
|
Упражнение 3.21. |
r |
|
|
r |
|
r |
|
|
|
|
|
||||||
Вычислить |
r |
+ |
|
r |
r |
r |
r |
если |
r |
r |
=А. |
||||||
a |
2b −c, 3a −b, 2a |
+ 2b |
+c , |
a,b,c |
|||||||||||||
Упражнение 3.22 |
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
r |
r |
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть a, b, c – некомпланарные векторы. Найти значение λ, при котором следующие |
|||||||||||||||||
|
|
|
|
|
|
|
r |
r |
r |
|
r |
r |
r |
r |
r |
− |
r |
векторы компланарны: p = a − |
2b |
+λc, |
q = |
3a +b −c, |
r = a |
λc. |
|||||||||||
|
|
|
|
|
|
|
|
Задачи для самостоятельного решения |
|||||||||
1. Даны векторы |
ar = (1; −2; 3), |
|
br = (1; 0; −3), |
c = (0; 4;1). |
Вычислить: а)[ar+2b, ar−cr]; б) |
||||||||||||
ar,br |
|
,cr |
− ar, br,cr |
; в) |
[ar,br], [ar,cr] . |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2.Вычислить 
ar, br, cr
, если 
2ar −b, ar +3br +cr, br −cr
= 5. Ответ: −95 .
3. При каких λ векторы ar = (3; −1; 4), b = (1; 0; 3), c = (λ; 2; λ −1), взятые в указанном порядке, образуют правую тройку?
4.Вычислить 
2ir−3rj +5k , ir+ rj, 2 rj −kr
.
Отметим, что векторное и смешанное произведение векторов (наряду со скалярным произведением) используется не только для вычисления площадей и объёмов, но является одним из основных инструментов для исследования прямых и плоскостей в пространстве (задач на составление уравнений прямых и плоскостей, взаимное расположение прямых и плоскостей и т.д.).
33