Векторное произведение

следующему условию: если смотреть из конца вектора c, то кратчайший поворот от вектора a

к вектору br осуществляется против часовой стрелки. Иначе ar,b,cr – левая тройка. Система

координат Oxyz – правая, если базисные векторы i,

rj, kr образуют правую тройку, и левая, если

ri, rj, kr– левая тройка.

r

r

r

Векторным произведением векторов a и b

(обозначается [a, b] или a

×b ) называется

вектор cr

такой, что выполняются условия:

r

r r

(1)

c a, b;

cr

= Sr r

(2)

a,b

(длина этого вектора равна площади параллелограмма, построенного на векторах ar и b );

r r r

(3)

векторы a,b,c образуют правую тройку.

r

r r

однозначно.

Замечание. Очевидно, условия (1) – (3) определяют вектор c

= a, b

Условие (3), конечно, относится к случаю, когда векторы a и b

неколлинеарны. Если ar

b, то

r r

r

условие (2) показывает, что a, b

= 0.

Свойства векторного произведения векторов:

r r

r r

(антикоммутативность);

(4)

[a, b] = −[b, a]

27

r

r r

r r r

r

(5)

[a

+b, c] =[a, c] +[b, c] (дистрибутивность);

r r

r r

).

(6)

[λa,b] = λ[a,b] ( λ

векторов по первому аргументу. Имеет место также линейность по второму аргументу:

r r r

r r

r

r

r

r

r r

(7)

[a, b +c] =[a, b] +[a, c],

[a, λb] = λ[a, b].

Условие коллинеарности векторов

r r

r

r

a, b коллинеарны

[a, b] = 0;

Выражение векторного произведения через

координаты векторов

Пусть ar = (a1; a2

r

= (b1; b2 ; b3 )

– векторы, заданные своими координатами в

; a3 ), b

прямоугольной системе координат, и

r r

r

i,

j, k – правая тройка. Тогда:

r r

=

ir

rj

kr

.

(8)

a, b

a

a

2

a

1

3

b1

b2

b3

Если раскрыть определитель, то получится:

r

r r

r

r

[a, b] = (a2b3

−a3b2 )i +(a3b1

−a1b3 ) j

+(a1b2 −a2b1)k.

(9)

Или, что тоже самое:

r r

a

a

a

a

a

a

=

b b

; −

b b

;

b b

.

a, b

2

3

1

3

1

2

2

3

1

3

1

2

Упражнение 3.13.

Найти векторное произведение векторов

и

с помощью определителя

стандартной функцией cross(a,b)

третьего порядка см формулу (8) и проверить решение1,2,0

b

2,1,0

Упражнение 3.15.

Упростить выражение

r

+

r

r

a

2b, a

−2b . Затем найти скалярное

произведение тех же векторов.

>> syms a1 a2 a3 b1 b2 b3

>> a=[a1 a2 a3];b=[b1 b2 b3];

>> ans1= cross(a,b)

>> ans2=cross(a+2*b,a-2*b)

>> simplify(ans2)

>>ans2./ans1

>> simplify(ans)

ans =

[ -4, -4, -4]

2

4 ,

Вывод

2 ,

Вывод.

Скалярное произведение тех же векторов преобразуется к совершенно иному

виду, а именно,

.

Упражнение 3.16.

Найти векторное произведение векторов

и

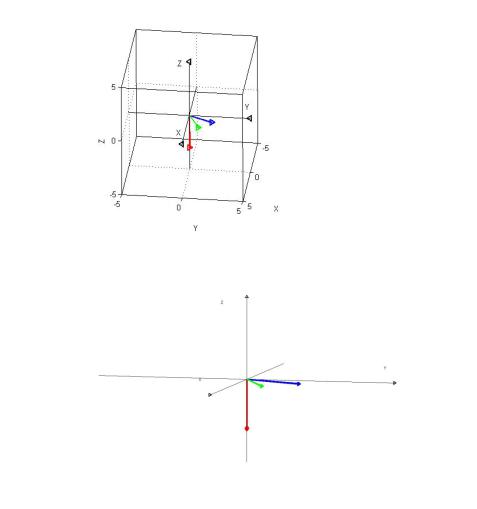
. Изобразить все данные и

результат. Первый вектор изобразить синим, второй

зеленым, результат красным. Сделать выводы: как

1,2,0

b

2,1,0

связаны определение векторного произведения и то, что мы получили на рисунке.

>> a=[1,2,0];b=[2,1,0];

// Задаем векторы

>> c=cross(a,b)

// Находим векторное произведение

c =

0 0

-3

// Нашли векторное произведение.

>> line([0 1],[0,2],'LineWidth',2)

//первый вектор

, по умолчанию цвет синий

>> plot3(1,2,0,'>','LineWidth',2)

//конец вектора a, по

умолчанию цвет синий

1,2,0

2,1,0

>> line([0 2],[0,1],'Color','green','LineWidth',2)

// второй вектор

.

>> plot3(2,1,0,'>g','LineWidth',2)

// конец вектора b

>> line([0 0],[0,0],[0 -3],'Color','red','LineWidth',2)

// результат

векторного произведения

c a b

0,0, 3

b

>> plot3(0,0,-3,'>r','LineWidth',2)

// конец вектора

>> plot3(5,0,0,'<k','LineWidth',2)

// направление оси 0Xc

>> plot3(0,5,0,'<k','LineWidth',2)

// направление оси 0Y

>> plot3(0,0,5,'<k','LineWidth',2)

// направление оси 0Z

>> text(4.5,-0.5,0.8,'X')

// подпись оси 0X

>> text(-0.5,4.5,0.8,'Y')

// подпись оси 0X

>> text(-0.5,-1,4.5,'Z')

// подпись оси 0Z