Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Московский государственный университет экономики, статистики и информатики (МЭСИ)

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математический анализ

.pdf

Скачиваний:

Добавлен:

05.06.2015

Размер:

4.32 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3313 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

4. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Если корни х1 и х2 квадратного трехчлена ax2+bx+d действительные и х1≠х2, то ax2+bx+d=a(x-x1)(x-x2) и для вычисления интеграла (4.53) пользуемся третьей подстановкой Эйлера

ax2	+ bx + d =	a(x − x1 )(x − x2 )=t(x-x1)	(4.64)
или		a(x − x1 )(x − x2 )=t(x-x2).
ax2	+ bx + d =	a(x − x1 )(x − x2 )=t(x-x2).	(4.65)

Если возвести обе части(4.64) в квадрат и найти х через новую переменную t, то получим

x =	x	t 2	− ax	2
	1			2
		t 2	− a
		t 2	− a

ax2 + bx + d

,dx = 2a(x1 − x2 )t dt,

(t 2 − a 2 )2

= a(x1 − x2 ) t. t 2 − a

(4.66)

(4.67)

Тогда, как нетрудно заметить, с учетом (4.66), (4.67) интеграл(4.53) принимает вид

t 2 − ax

a(x1

− x2 )t

(x1 − x2 )t

2a ∫R

dt.

− a

− a)

− a

В заключение этого пункта получим формулу (4.25) с помощью первой подстановки Эйлера (4.54).

Рассмотрим ∫	x	2dx	2 . Так как многочлен второй степени под квадратным корнем
	x	±a

не имеет действительных корней и коэффициент при х2 имеет положительный знак, то пользуемся первой подстановкой Эйлера

x 2 ± a 2 =t-x.

Отсюда x=

t 2 ma 2

, dx=

t 2 ±a 2

dt,

2t 2

± a

t 2 ±a 2

2t (t 2 ±a 2 )

∫ x2dx±a 2

= ∫

dt = ∫dt =ln

+C=ln x + x2

± a 2

+ C,

(t 2

±a 2 ) 2t 2

что совпадает с (4.25).

120

4. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Примеры

Пример 1. Вычислить

∫

(2 3 x + 1)ln (3 x + 2 )dx , x>0.

(4.68)

33 x 2

Решение:

Заменяя,

что

= d 3 x

и введя новую переменную по формуле

33 x 2

3 x = y , (4.68) перепишем в виде

∫(23 x +1) ln(3

x + 2)d 3

x = ∫(2 y +1) ln( y + 2)dy .

(4.69)

Интеграл

(4.69),

вычислим

методом

интегрирования

по частям, взяв

U = ln( y + 2), dU =

и dV = (2 y +1)dy,

V = y2 + y .

y + 2

Тогда, согласно (4.19), имеем

∫(2 y +1) ln( y + 2)dy = ( y 2 + y) ln( y + 2) − ∫

y 2 + y

dy .

(4.70)

y + 2

Второй член в правой части (4.70) представляет собой неопределенный интеграл от

неправильной рациональной дроби

2 +

y +

Выделяя в этой дроби целую часть (см. пункт 4.5.) и представляя ее в виде

y 2 +

= y

− 1

после

вычисления

y +

∫

y 2 + y

dy =

y 2

− y + 2 ln( y + 2) + C, из (4.70) получим

y + 2

∫(2 y +1) ln( y + 2)dy = ( y 2

+ y) ln( y + 2) −

y 2

+ y − 2 ln( y + 2) + C .

Теперь остается перейти к переменной x в (4.71).

интеграла

(4.71)

Ответ: ∫	(23	x +1) ln(3 x + 2)			dx = (3 x2 + 3 x − 2) ln(3 x + 2) −	1	3	x2 + 3 x + C.
		3	x	2		2
		3

121

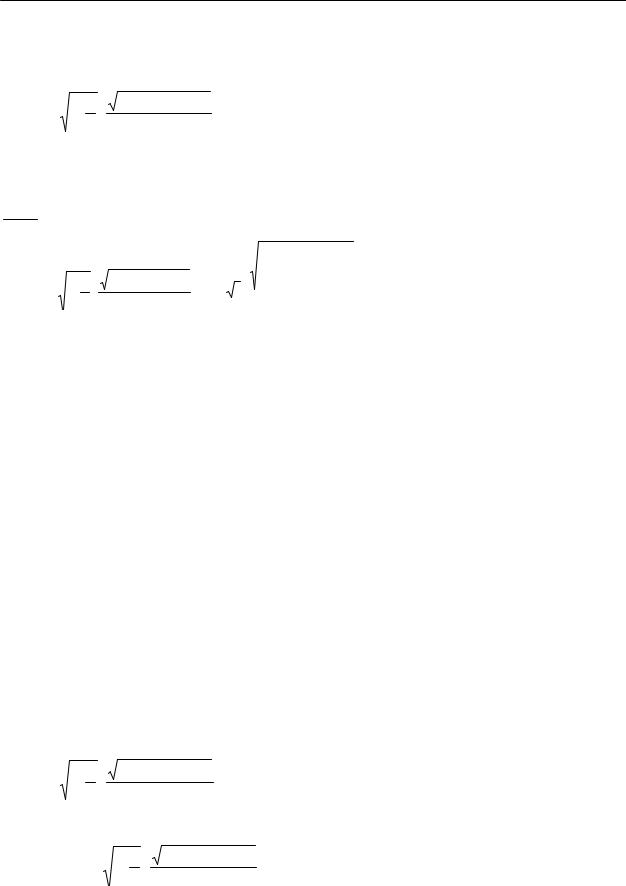
4. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

1 + t 2

Пример 2. Вычислить
∫ tg x		sin x(1 + cos x)dx , 0 ≤ x ≤		π .		(4.72)
2		sin x +1		2
Решение: Применяя подстановку (4.44) с учетом x = 2arctgt, dx =					2dt	, sin x =
					1 + t 2	, sin x =
	1−t 2				1 + t 2
, cos x =	1−t 2		получим

	1	+ t 2
	1	+ t 2

1−t

sinx(1+cosx)

1+t

2dt

tdt

∫

dx=∫

=4∫

sinx +1

(4.73)

1+t2

(t +1)2 (t2 +1)

1+t2

Подынтегральная

функция в (4.73) является правильной рациональной дробью от-

носительно переменной t. Представим ее в виде суммы простейших правильных дробей

методом Лагранжа (см. (4.35)).
Имеем
	t	=	A	+	B	+	Et + D	,	(4.74)
	(t +1)2 (t 2 +1)	=	t +1	+	(t +1)2	+	t 2 +1	,	(4.74)
	(t +1)2 (t 2 +1)		t +1		(t +1)2		t 2 +1

что приводит к системе линейных уравнений для определения неопределенных коэффи-

циентов A, B, E, D:

A + B = 0,

t 2

A + B

+ 2E + D = 0,

(4.75)

A + E

+ 2D =1,

+ D = 0.

A + B

Решая систему (4.75), получим А=0, В = −

, Е = 0, D =

. Тогда вместо интеграла

(4.73) будем иметь

4∫

tdt

= −2∫

2∫

2(t +1)

−1

+ 2arctgt + C .

(t +1)

+1)

(t +1)

Возвращаясь к старой переменной, получим

∫

tg x

sin x(1 + cos x) dx

+ x + C .

sin x +1

Ответ: ∫

tg x

sin x(1 + cos x) dx =

+ x + C .

sin x +1

122

			4. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пример 3. Вычислить:
dx	.			(4.76)
∫x3 1 + x5

Решение: Если перепишем (4.76) в виде
∫x−1 (1+ x5 )−		1	dx ,	(4.77)
		3

то заметим, что под интегралом в (4.77) стоит дифференциальный бином (см. пункт 4.7),

причем m=-1, n=5, p = −												1	и		m +1		= 0 – целое число. Для вычисления интеграла (4.77)
причем m=-1, n=5, p = −												3	и			n	= 0 – целое число. Для вычисления интеграла (4.77)
												3				n
делаем подстановку (4.52).
Итак имеем
					(1+x5) −						1								1							3			4
1+x5 = t3 ,													= t-1,			x = (t3 -1)					,		dx =				(t3		– 1) −		t2 dt .	(4.78)
											3									5										5
											3									5					5					5
Тогда (4.77) с учетом (4.78) принимает вид																									5
Тогда (4.77) с учетом (4.78) принимает вид
	3	∫(t	3		−	1	−1		3				−	4	2		3	∫				tdt						.				(4.79)
	3		3	−1)		5 t	−1	(t	3	−1) 5 t					2	dt =	3					tdt
5				−1)		5 t		(t		−1) 5 t						dt =	5		(t −1)(t				2	+ t	+1)
5																	5		(t −1)(t					+ t	+1)
Функция										t						под интегралом в (4.79) представляет собой правильную
Функция					(t −1)(t 2						+ t +1)					под интегралом в (4.79) представляет собой правильную

рациональную дробь, которую можем представить в виде суммы простейших правильных рациональных дробей методом Лагранжа в виде

Bt + D

t −1

(t −1)(t 2 + t +1)

t 2 + t +1

Для определения пока неизвестных коэффициентов A, B, D получим систему урав-

нений

t 2

A + B = 0,

− B

+ D =1,

− D = 0.

Отсюда А =

, В =

−

, D =

и интеграл (4.79) принимает вид

(t −1)dt

tdt

∫

−

∫

t −1

−

∫

t −

+ t

t +

1 ln t −1 −

ln t

2 + t +1 +

3 arctg 2t +1

+ C =

(t −1)2

3 arctg

2t +1

+ C ,

t 2 + t +1

где t = 3 1+ x5 .

Ответ:

∫

5 =

ln 3

(3 1+ x5 −1)2

arctg

23 1+ x5 +1

+C.

1+x

)

1+ x

( 1+ x

123

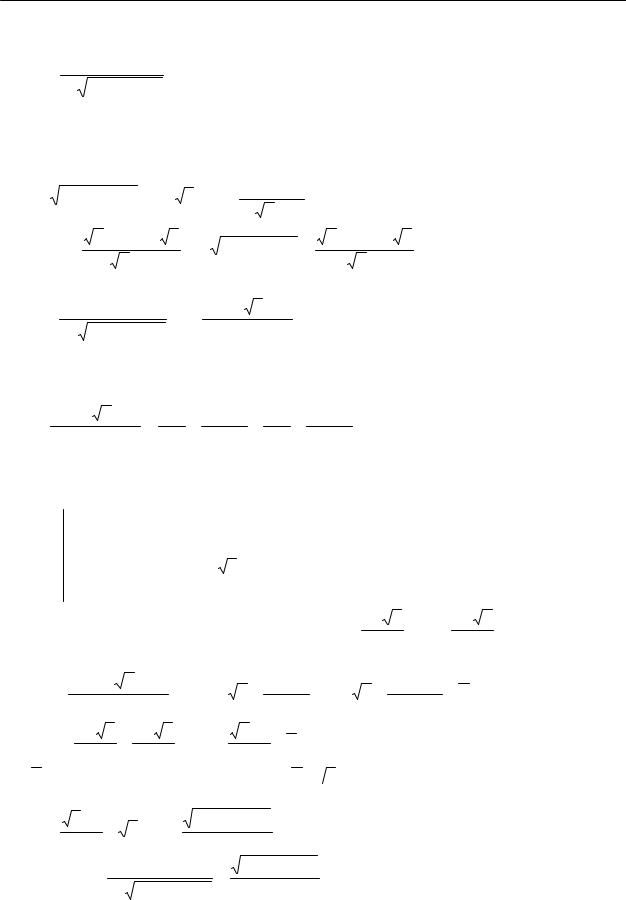
		4. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
Пример 4. Вычислить:
(x −1)dx
∫ x2 2x2 −2x +1	, x≠0.	(4.80)

Решение: Так как квадратный трехчлен 2x2 – 2x + 1 не имеет действительных корней (D = -4 < 0) и коэффициент при x2 положительное число (2 > 0), то для вычисления (4.80) можно пользоваться первой подстановкой Эйлера (4.54).

Имеем

2x2 − 2x +1 = t − 2x , x =

t 2 −1

2( 2t −1)

dx =

2t 2

− 2t +

2 dt ,

2x2

− 2x +1 =

2t 2

− 2t + 2 .

(4.81)

2t −1)2

2t −1)

Тогда с учетом (4.81) интеграл (4.80) принимает вид

∫

(x −1)dx

= 2∫

t 2

− 2 2t +1

(4.82)

− 2x +1

(t −1)

(t +1)

2 dt .

Для вычисления (4.82) разложим подынтегральную правильную рациональную дробь на простые правильные рациональные дроби с неопределенными коэффициентами в виде

t 2 − 2 2t +1

(4.83)

(t −1)2 (t +1)2

t −1

(t −1)

t +

(t +1)2

Приведя правую часть (4.83) к общему знаменателю и приравнивая коэффициенты при одинаковых степенях t справа и слева в знаменателях (4.83), получим следующую систему линейных уравнений для определения коэффициентов A, B, C, D.

A + E = 0,

t 2

+ D =1,

A + B − E

(4.84)

− A + 2B − E − 2D = −2 2,

− A + B + E + D =1.

Решая систему (4.84), получим А = E = 0, В =

1 −

2 ,

D =

1 + 2

. Тогда вместо ин-

теграла (4.82) будем иметь

2∫

t 2

− 2

2t +1

2)∫

+ (1 + 2)∫

+ C =

(t +

+1)

2 dt = (1

−

(t −1)

= −

1 −

− 1 + 2 + C =

2 −t

+ C ,

(4.85)

t −1

t +1

t 2 −1

где С – производная постоянная . Взяв С= 2 +С, где С – производная постоянная , и переходя в (4.85) к переменной x, окончательно получим

−t

2 + C =

2x2

−

2x +1

+ C.

t 2

−1

Ответ: ∫

(x −1)dx

2x2 − 2x +1

+ C.

− 2x −1

124

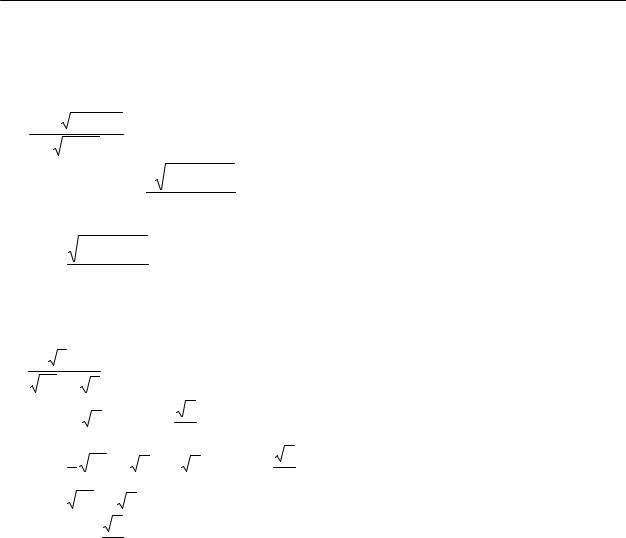
4. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

Тест 4

Вычислить неопределенные интегралы.

1. ∫

2x −

arcsin x

dx , -1<x<1.

1− x

а) −ln

1 − x

−

2 (arcsin x)3

+ c ;

б) ln|1-x2|+c;

в)

(arcsin x)3

+ c ;

г) - 2 x+c.

2. ∫

xdx

, x>0.

x2 +43

а)

+ x ;

966

x −192arctg

б)

2 + c ;

−

8 x + 96

x −192arctg

в) 6 x5 − 8 x + c ;

г)

+ c .

arctg

3. ∫(x2ex + ln 2 x)dx , x>0.

а) ex(x2-2x+2)+c; б) lnx(lnx-2)+c; в) xlnx+c;

г) ex(x2-2x+2)+xlnx(lnx-2)+2x+c.

4. ∫x3ch3xdx .

а)

+c ;

sh3x

б)

sh3x

−

+c;

в)

sh3x

−

sh3x

+c ;

г)

sh3x +c .

125

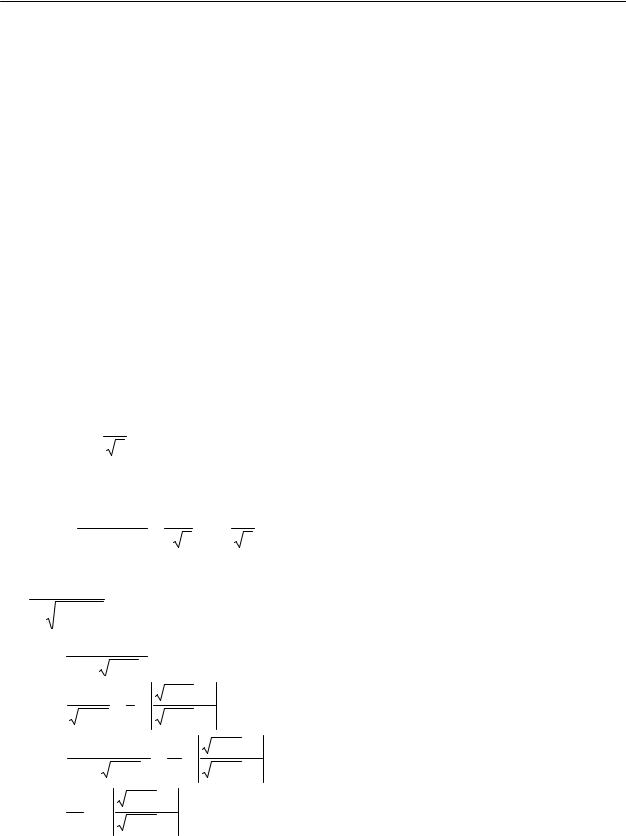
4. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

∫

−4 sin x +3cos x

а)

+c ;

2 − tg

б)

+c;

в) tg x +c;

г) −

+ c .

∫

(sin 2 x +2cos2

а) −

tgx

+c ;

4 tg2x +2

(

)

б)

arctg tgx + c ;

в)

+c ;

tg2x +2

г) −

(

tgx

)

+ 3

arctg tgx + c .

4 tg2x +2

3 , x≠0, x≠-1.

7. ∫ x3

1 − x

(

)

а)

15x2

+5x −1

+c ;

4x2

1 + x

б)

1 ln 1 + x −1 + c ;

1 + x

1 + x +1

в)

15x2

+ 5x − 2

+ x −1

+ c ;

4x2

1 + x

+ x +1

г)

+ ln 1 + x −1 + c .

1 + x +1

126

4. НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

8. ∫ x3 + x4 dx , x>0.

(x + x

)

1 +2x

а)

−

x + x

8 ln x

+ 1 + x

+c ;

(x + x

)

x + x2

б)

−

+c ;

в)

1 ln x + 1 + x +c ;

1 +2x

x + x2 + 1 ln x + 1 + x +c .

г) −

9. ∫

9dx

, x≠±1.

(

)

−1

а)

2x6

−3x2

−1

+c ;

−1

б)

2x6

−3x2

−1

+c ;

−1

в)

8 ln|x -1|+c;

г) 3ln|x2+1|+c.

10. ∫

xdx

, x<1 U x>3.

(

)

− 3x + 2

− 4x

+ 3

а) ∫ d F ( x ) = F ( x ) + C ;

б)

arcsin

+c ;

x −

в)

−4x + 3

;

x −1

г)

−4x +3

−arcsin

+c .

x −1

x −

127

5. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИМЕНЕНИЕ

Раздел V. Определенный интеграл и его применение

5.1. Определение определенного интеграла

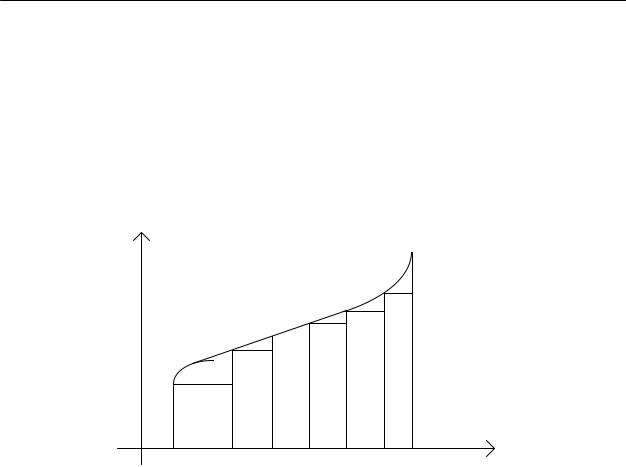
Рассмотрим геометрическую задачу вычисления площади криволинейной трапеции и покажем, как при ее решении приходим к понятию определенного интеграла.

Пусть на плоскости X0Y имеем криволинейную трапецию ABCD, ограниченную кривой y=f(x), определенной и непрерывной при x [a;b], и двумя прямыми x=a и x=b (см.рис.5.1).

y=f(x)

B
B
A		D
0 x =a	x1 x2 xi xi+1	x =b	x
0		n

Рис. 5.1.

Разделим основание AB этой трапеции на n частей произвольным образом(разбиение Т) и проведем ординаты соответствующих точек деления

x0=a<x1<x2<...<xi<xi+1<...<xn=b.

Точки x0, x1, x2,..., xi, xi+1,...,xn называются точками разбиения T.

Возьмем i-тую элементарную трапецию и заменим ее приближенно прямоугольни-

ком с основанием ∆xi=xi+1-xi и высотой f(ξi), где ξi абсцисса произвольной точки из сегмента [xi;xi+1]. Тогда площадь i-той трапеции приближенно равна площади i- того прямо-

угольника, т.е. Si≈f(ξi) ∆xi. Если суммировать площади всех элементарных прямоугольников (i=1,2,...,n), то получим приближенную площадь криволинейной трапеции ABCD в виде

n	(5.1)
SABCD ∑ f (ξ1 ) ∆xi

i=1

Очевидно, что точное значение криволинейной площади SABCD получим, если в (5.1) перейдем к пределу, когда max ∆xi→0 (n→∞), т.е.

S ABCD = maxlim 0 ∑ f (ξ)∆x . (5.2)

∆xi → i i=1

128

5. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ И ЕГО ПРИМЕНЕНИЕ

Последнее, как покажем ниже, по определению и есть определенный интеграл от

функции f(x) в пределах от a до b ( ∫f(x)dx ).

Определение 5.1. Сумма вида

n
I(xi,ξi)= ∑ f (ξi )∆xi =f(ξ1)∆x1+f(ξ2)∆x2+...+f(ξn)∆xn	(5.3)

i=1

называется интегральной суммой функции f(x), соответствующей данному разбиению Т сегмента [a;b] и данному выбору промежуточных точек ξi на частичных сегментах [xi-1,xi].

Определение 5.2. Конечный предел интегральных сумм функции f(x) при стремлении к нулю max ∆xi называется определенным интегралом от функции f(x) в пределах от a до b и обозначается так

b	n
∫f (x)dx = maxlim∆xi →0	∑f (ξ)∆xi .	(5.4)
a	i=1

5.2. Верхняя и нижняя интегральные суммы Дарбу и их свойства

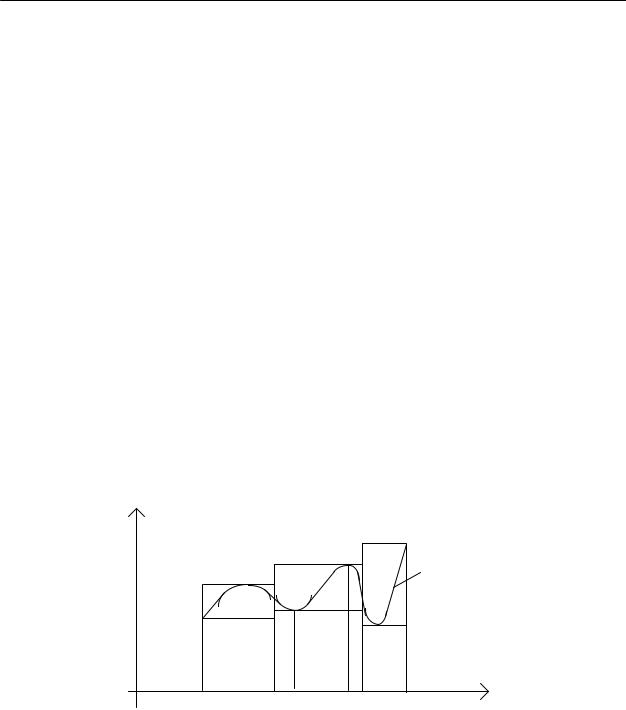
Пусть функция f(x) определена и ограничена на сегменте [a;b] и для этого сегмента имеем разбиение Т a=x0<x1<x2<...<xi-1<xi<...<xn.

Предположим, что Мi является точной верхней гранью, а mi - точной нижней гранью функции f(x) на i-ом элементарном сегменте [xi-1, xi] (см. рис. 5.2. для случая непрерывной функции f(x)).

M i	y=f(x)

m i

				xi




a		xi-1			b	x
a		xi-1			b	x
Определение 5.2. Суммы вида			Рис. 5.2.
Определение 5.2. Суммы вида
	n
S=M1∆x1+M2∆x2+...+Mn∆xn= ∑M i ∆xi ,
	i=1
	n
s=m1∆x1+m2∆x2+...+mn∆xn= ∑mi ∆xi ,						(5.5.)

i=1

называются, соответственно верхней и нижней интегральными суммами Дарбу функции f(x) для данного разбиения Т сегмента [a,b].

129

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 1213 / 3313 14 15 16 17 18 19 20 21 22 23 24 25 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
05.06.20153.06 Mб20мат мет.doc
#
05.06.201520.22 Кб10МАТ.АНАЛИЗ.docx
#
05.06.2015297.47 Кб109мат_МЕТОД_ИССЛЕД_ОПЕРАЦ.doc
#
05.06.2015166.91 Кб15Математика-1.doc
#
05.06.20152.97 Mб28Математический анализ для экономистов.doc
#
05.06.20154.32 Mб77Математический анализ.pdf
#
05.06.2015429.57 Кб27материалы для курсового лекции.doc
#
01.05.2025166.93 Кб0Материалы к курсу Международные инвестиции_.docx
#
05.06.20151.76 Mб290Матлогика Пономарев.pdf
#
05.06.2015113.15 Кб12медиабизнес.doc
#
05.06.20155.68 Mб54Медиарекламные исследования.pdf