Математический анализ

1. ТЕОРИЯ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Решение: б) При x → 3 числитель и знаменатель этой дроби б.м.ф., то есть имеет

место неопределенность типа 00 . Число 3 является корнем и многочлена, стоящего в

числителе, и многочлена, стоящего в знаменателе. Разлагая числитель и знаменатель на простые множители, получим:

есть в данном случае числитель и знаменатель этой дроби б.м.ф. при x →1 и имеем неоп-

Ответ: ∞ .

42

1. ТЕОРИЯ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Решение: д) Числитель и знаменатель этой дроби б.м.ф. при x → 0 . То есть имеем

ленностью типа [1∞ ]. Для ее раскрытия пользуемся вторым замечательным пределом, предварительно выполняя следующие преобразования:

Ответ: e12 .

Пример 3. Найти точки разрыва следующих функций:

Решение: а) Нетрудно заметить, что для всех точек числовой оси, кроме точки x = 0 условие непрерывности (1.46) выполняется. А что происходит в точке x = 0? Так

43

1. ТЕОРИЯ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

ной функции. Таким образом, заданная функция в точке x = 0 нарушается условие непрерывности заданной функции. Таким образом, заданная функция в точке x = 0 имеет устранимый разрыв.

Ответ: в точке x = 0- устранимый разрыв.

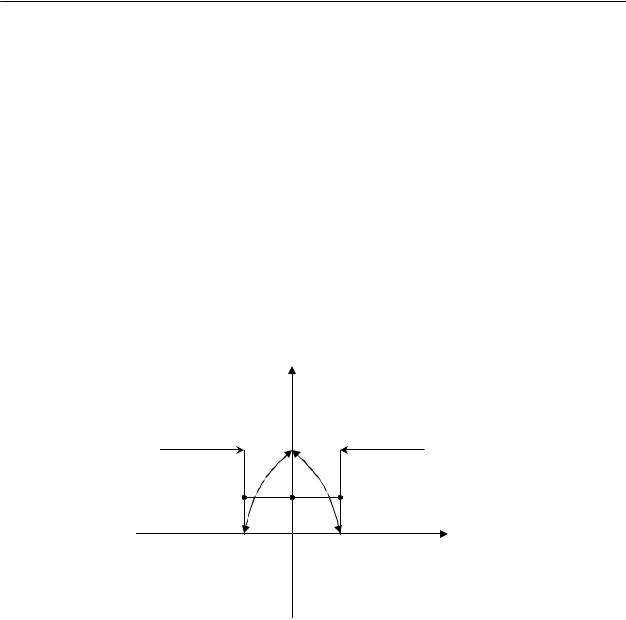
Решение: б) Непрерывность данной функции во всех точках числовой оси, кроме точек 0; -2;+2, очевидна. А что происходит в точках 0;-2;2? Проверим условие непрерыв-

f (0) = 2 . Значит точка x = 0 для данной функции является точкой разрыва первого рода. Теперь проверим условие непрерывности (1.46) для данной функции в точках x=2 и

f(x)

Рис. 1.12.

Ответ: в точках, x=2, x=-2- разрыв первого рода, в точке x=0 -устранимый разрыв.

Решение: в) Очевидно, что рассматриваемая функция является непрерывной во всех точках числовой оси, кроме точки x=2, которая не входит в область ее определения. Определим характер разрыва данной функции в точке x=2. Имеем

Следовательно, точка x=2- точка разрыва первого рода. Ответ: точка x=2 – точка разрыва первого рода.

Решение: г) Очевидно, что заданная функция непрерывна на всей числовой оси кроме точки x=0 (она не входит в область определения функции). Определим характер разрыва заданной функции в точке x=0. Имеем

44

1. ТЕОРИЯ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Так как один из односторонних пределов (в данном случае правосторонний) не равен конечному числу, то точка x=0 для данной функции является точкой разрыва второго рода.

Ответ: точка x=0 – точка разрыва второго рода.

Пример 4. Определить порядок малости б.м.ф. f(x) по отношению к основной бесконечно малой ϕ(x)=x при х→0.

а) f(x)=2(ex3 -1) при х→0; ϕ(x)=x при х→0.

б) f(x)=ln(sin x2+1) при х→0; ϕ(x)=x при х→0.

Решение: а). Пусть функция f(x)=2(ex3 -1) б.м.ф. порядка n по отношению к основной бесконечно малой ϕ(x) = x при x →0. Тогда по определению (1.28.) и с учетом того,

Отсюда заключаем, что б.м.ф. f(x)=2(ex3 -1) бесконечно малая третьего порядка по отношению к основной бесконечно малой x при x → 0 .

Ответ: ex3 -1 бесконечно малая третьего порядка по отношению к бесконечно малой x при x→ 0.

Решение: б) Рассуждая аналогично примеру а) имеем

Ответ: ln(sin x2 + 1) бесконечно малая второго порядка по отношению к бесконечно малой x при x→0.

45

1. ТЕОРИЯ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

Тест 1

а) 0; б) ∞; в) 5 г) 3.

4. limx→∞ x[ln(3x −1)− ln(3x −2)].

а) ∞; б) 0;

в) 13 ; г) 2.

3

5. lim(1 +cos x)cos x .

x→π2

а) 1;

б) е3;

в) e; г) 0.

6. lim x + 4 −3x . x→∞ x + 8

а) 1;

46

1. ТЕОРИЯ ЧИСЛОВЫХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ И ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ

б) ∞;

в) е; г) е12.

а) 0; б) 2;

в) 12 ; г) 5.

Определите порядок б.м.ф. f(x) по отношению к б.м.ф. ϕ(х):

8. f(x)= x(x +1) , ϕ(x)=x, x→0. 1 + x

а) 1; б) 3; в) 4; г) 6;

9. f(x)= 1 + x2 tg π2x , ϕ(x)=x, x→0.

а) 2; б) 1; в) 3; г) 4.

Найти точку разрыва функции и определить его характер: 10. f(x)= xx .

а) х=0 – точка разрыва первого рода; б) х=0 – точка разрыва второго рода; в) х=0 – точка устранимого разрыва.

47

2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Раздел II. Дифференциальное исчисление функции одной переменной

2.1. Определение производной функции первого порядка

Пусть функция y=f(x) определена в некоторой окрестности точки х0 и пусть х0+∆х, где ∆х есть приращение аргумента, есть некоторая точка этой окрестности.

Определение 2.1. Если существует предел отношения ∆y = f(x0 + ∆x)− f(x0 ) при

∆x ∆x

∆х→0, то этот предел называется производной первого порядка функции y=f(x) в точке х0 и обозначается так:

говорят, что для этого значения х0 существует бесконечная производная, равная соответственно +∞; -∞; ∞.

ной или бесконечной правосторонней (левосторонней) производной функции y=f(x) в точке х=х0 и обозначается так:

Теорема 2.1. Функция y=f(x), определенная в некоторой окрестности точки х=х0, имеет конечную производную f′(x0) тогда и только тогда, когда существуют равные друг другу конечные правосторонняя и левосторонняя производные этой функции в точке х0,

т.е. когда f′(x0+0)=f′(x0-0). В этом случае f′(x)= f′(x0+0)=f′(x0-0).

Заметим, что доказательство этой теоремы следует из теоремы 1.16 об односторонних пределах.

2.2. Геометрический смысл производной.

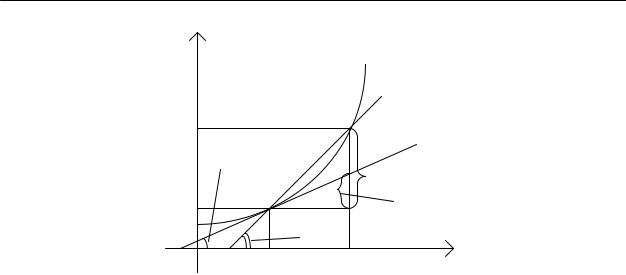
Пусть функция y=f(x) определена и непрерывна на некотором интервале (а;b) и имеет конечную производную в точке x0 (a;b). Рассмотрим график этой функции

(рис. 2.1.).

47

2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

y

A

Рис. 2.1.

На графике точка А0 имеет координаты А0[x0;f(x0)], а точка А – координаты A[x0+∆x; f(x0+∆x)], где приращение аргумента ∆х>0 и x0+∆x (a;b). Через ϕ(∆х) обозначим

Заметим, что при стремлении точки А к точке А0 по графику, т.е. при стремлении ∆х к нулю, секущая А0А займет свое предельное положение, совпадающего с касательной к графику в точке х0. При этом ϕ(∆х)→ϕ(х0), где ϕ(х0) есть угол между касательной к графику в точке х0 и положительным направлением оси 0х. Итак, учитывая вышесказанное,

(2.4) показывает, что производная функция y=f(x) первого порядка в точке х0 равна тангенсу угла между касательной к графику функции y=ϕ(x) в точке х0 и положительным направлением оси 0х.

2.3. Дифференцируемость функции. Дифференциал функции и его геометрический смысл

Пусть функция y=f(x) определена на интервале (a;b), х – некоторое фиксированное значение аргумента, ∆х – любое приращение аргумента такое, что (х+∆х) (a;b).

Определение 2.3. Функция y=f(x) называется дифференцируемой в точке х, если приращение ∆у=∆f(x) этой функции в точке х, соответствующее приращению аргумента ∆х, может быть представлено в виде

где А – константа, не зависящая от ∆х, а α(∆х) – является бесконечно малой при ∆х→0.

48

2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

Заметим, что функция α(∆х) при ∆х=0, вообще говоря, не определена. Поэтому в этой точке приписываем значение α(0)=0, чтобы функция α(∆х) стала непрерывной в точке ∆х=0. Тогда равенство (2.5) можно распространить и на значение ∆х=0. Заметим также, что так как α(∆х) и ∆х бесконечно малые при ∆х→0, то α(∆х) ∆х=0(∆х), т.е. второй член в (2.5) бесконечно малая величина более высокого порядка, чем ∆х. С учетом того (2.5) можно переписать в виде

Теорема 2.2. Для того, чтобы функция у=f(x) являлась дифференцируемой в точке х (символически это записывается так: f(x) C′(x)), необходимо и достаточно, чтобы она

Последнее, по определению 2.1 означает, что y′=f′(x)=A.

Достаточность.

Дано: конечная y′=f′(x). (2.9)

Доказать: ∆у=А ∆х+α(∆х) ∆х. (2.10)

Из (2.9) с учетом (1.36) имеем

∆∆yx − f ′(x)= α(∆x) или ∆y=f′(x) ∆x+α(∆x) ∆x, (2.11)

где α(∆х)→0 при ∆х→0.

Если теперь постоянную величину f′(x) обозначить через А, то (2.11) перепишется

в виде

∆y=A ∆x+α(∆x) ∆x,

что и доказывает дифференцируемость функции y=f(x).

Теорема 2.3. Если функция y=f(x) дифференцируема в точке х, то она непрерывна в этой точке.

Из (2.12) следует, что

∆y=f′(x) ∆x+α(∆x) ∆x.

49

2. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

прерывности (см. определение 1.34) функция y=f(x) непрерывна в точке х.

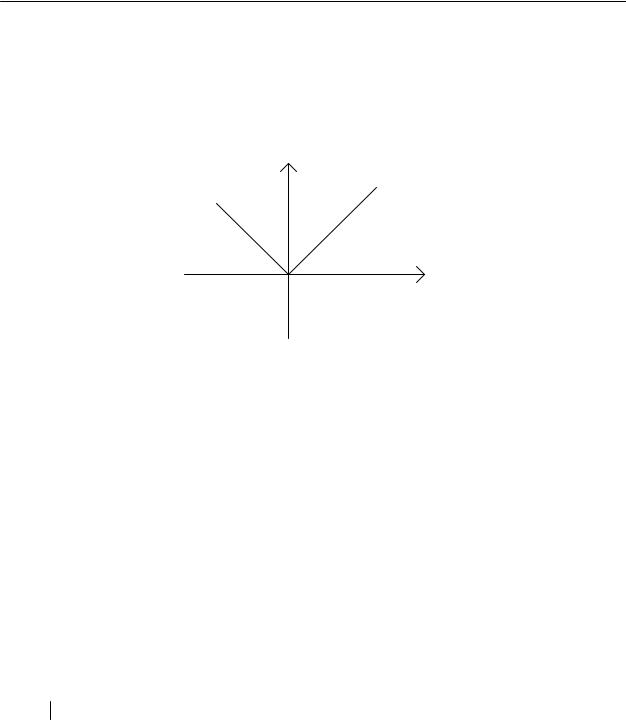
Отметим, что обратное утверждение, не имеет места, т.е. непрерывная в точке х функция не обязательно является дифференцируемой в этой точке. Для примера, рассмотрим функцию у=|x|, график которой приведен на рисунке 2.2.

y

y=|x|

Рис. 2.2.

Поскольку ∆у=|x+∆x|-|x|≤|x+∆x-x|=|∆x| и lim ∆y = 0 , то функция y=|x| непрерывна в

∆x→0

любой точке x (-∞;+∞). Покажем, что эта функция в точке х=0 не имеет производной. Действительно, так как

и правосторонняя производная функции в точке х=0 отлична от левосторонней производной, т.е. функция y=|x| в точке х=0 не имеет конечной производной. В остальных точках конечная производная функции y=|x| существует и равна

Теперь перейдем к определению понятия дифференциала функции y=f(x). предполагая, что y=f(x) C′(x), на основании теоремы 2.2 имеем

Пусть f′(x)≠0, т.е. первое слагаемое в (2.14) является главной линейной относительно ∆х частью приращения дифференцируемой функции.

50