3. Обратное интерполирование

Одним из важных аспектов применения интерполяционной формулы Лагранжа является решение так называемой задачи обратного интерполирования — нахождения приближенного значения по известному значению. Речь здесь пойдет, в первую очередь, о таблично заданных функциях, для которыхне совпадает ни с одним узлом. Формально можно поступить следующим образом: построить обратную функциюи по заданномунайтипо формуле

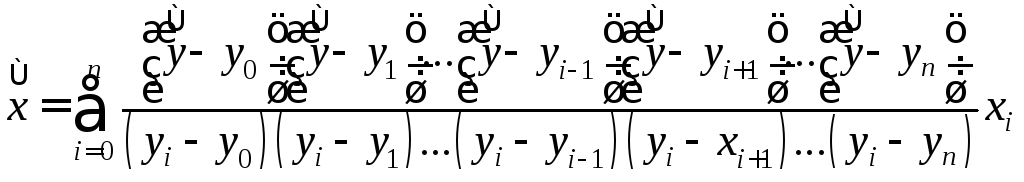(39)

т.е. поменяв в формуле (9) значения функции и аргумента. Это нетрудно проделать для многочленов небольших степеней, однако процесс заметно усложняется при увеличении степени. Если же степень многочлена заранее неизвестна, то наиболее приемлемы интерполяционные формулы Ньютона, Бесселя и Стирлинга.

Поступаем следующим образом. Выбираем базовый узел , наиболее близкий к заданному значению. Предполагая, что функциямонотонна, анаходим допуская его близость к, т.е. его находят из соответствующих интерполяционных формул путем последовательных приближений (итераций) длины интервала, из которого следует.

Пусть, например, , т.е. находится в середине диагональной таблицы разностей, и, следовательно, применима любая из центральных интерполяционных формул. Из формулы

выражаем

и строим итерационный процесс

(40)

при k=0, 1, 2… , начиная с . Количество членов в формуле (37) можно зафиксировать в соответствии с поведением конечных разностей, а сам итерационный процесс продолжаем до выполнения условия , где - наперед заданная погрешность вычисления.

Аналогичные формулы можно получить исходя, из других интерполяционных выражений. Например, если и находится в начале диагональной таблицы разностей, то подходящей для обратного интерполирования итерация будет

(41)

Пример 5. Пусть функция y=y(x) задана в виде таблицы (см. пример 4 из предыдущего параграфа). Требуется найти приближенно корень уравнения y=0 с точностью =0,01.

Решение.

1. По диагональной таблице разностей определяем, что искомый интервал , так как, и можно применить любую из полученных формул (40) или (41).

2. Полагая, что ,,n=3, в соответствии с формулой последовательных приближений (41) и данными таблицы примера 4, находим:

Видно, что разность , следовательно, итерационный процесс можно завершить, и искомое .

Решение задачи с использованием формулы (40) предлагается сделать читателю самостоятельно.

0. Интерполяцияс кратными узлами. Полиномы Эрмита

При решении инженерных и экономических задач часто возникает задача восстановления интерполяционного многочлена по известным значениям функции и производным в равноотстоящих узлах. Приведем два примера.

1. Пусть переменное движение материальной точки описывается по неизвестному закону . При этом известно: координаты точек,,…,; скоростей,,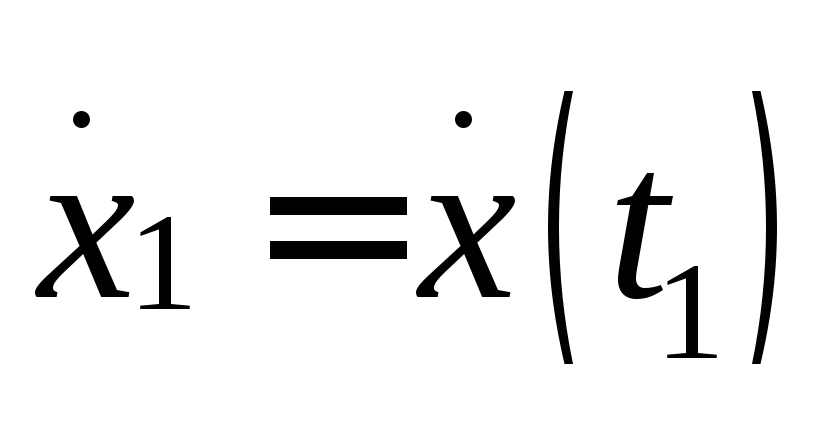…,; ускорений,,…,;...и т.д. до,,…,. Требуется по заданным значениям найти закон движения.

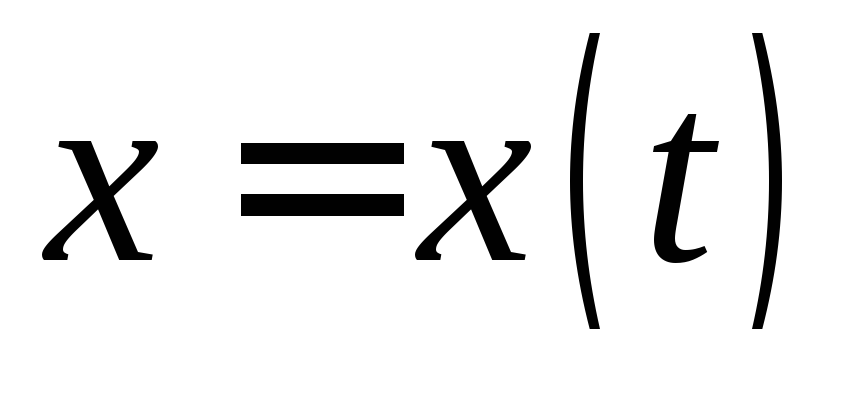2. Пусть объем произведенной продукции описывается неизвестной функцией . При этом известно: количество продукции,,…,; производительность труда,,…,. При этом некоторые данные могут отсутствовать. Требуется по заданным значениям восстановить неизвестную функцию и значения.

Итак, имеем следующую постановку задачи.

Пусть функция задана в равноотстоящих узлах, где, и имеется информация о значениях производных произвольного порядка в этих точках, то есть

, ,,….,— всегозначений;

, ,,….,— всегозначений;

, ,,….,— всегозначений;

… … … … … … … … …

, ,,….,— всегозначений.

В общем случае , кроме того, информация об промежуточных производных может отсутствовать.

Необходимо получить явный вид функции .

Будем называть узел , в котором определенапроизводная, узлом кратности; узелв котором определена- производная, узлом кратности; и т.д… узелв котором определена- производная, узлом кратности.

Решение задачи о нахождении явного вида функции будем называть задачей о кратных узлах, а сам полином, аппроксимирующий функцию — полиномом Эрмита.

Поиск общего вида интерполяционного многочлена Эрмита представляет сложную задачу и требует привлечения математического аппарата теории функции комплексного переменного и выходит за рамки настоящего курса.

Можно показать, что искомый многочлен будет n-ой степени, которая определяется из равенства , а его аналитическая форма определяется выражением

(42)

где - многочлен Лагранжа m-ой степени, построенный по m известным значениям функции ,-многочлен степени m+1.

Формула (42) составлена из следующих соображений. В узлах, при , где, второе слагаемое равно нулю, и значения функции в этих точках равны. Таким образом, выражение (42) представляет собой выделение многочлена Лагранжа из многочлена Эрмита, а второе слагаемое степениn должно обращаться в нуль в узловых точках и состоит из произведения многочлена m+1 степени¹ и неизвестного многочлена , для определения которого продифференцируем (42)

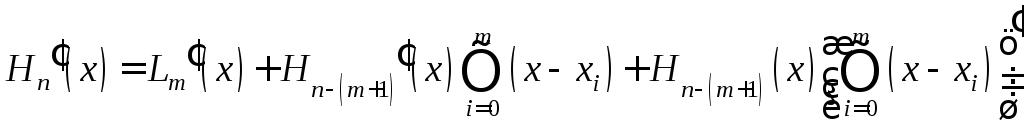(43)

В узловых точках, второе слагаемое равно нулю, и

(44)

Если информация об интерполируемой функции исчерпывается данными об ее первых производных, то формула (41) будет окончательной и достаточной для восстановления неизвестной функции простым методом Лагранжа. Если известны производные более высоких порядков, то процесс дифференцирования (39) продолжают - раз, т.е. до максимальной кратности.

Пример 6. Пусть некоторая функция задана в виде

i	x
0	34	36	32	4
1	36	38	30
2	38	31	1	8

Требуется найти многочлен Эрмита, для которого: ;;, для.

Решение.

1. Определяем кратность каждого узла и кратность интерполирующего многочлена. Имеем: m=2; ; ; , откуда .

2. Общий вид многочлена Эрмита будет

.

Интерполяционный многочлен Лагранжа находим по формуле (11)

следовательно,

(*)

3. Так как максимальная кратность равна 2, то, дифференцируя дважды (*), получаем

Из полученных формул получаем

4. Сведем полученные данные о многочлене в таблицу

i	xi
0	34
1	36
2	38

Определяем кратность каждого узла и уточняем кратность многочлена . Имеем: m=2; ; ; , откуда .

5. Общий вид многочлена Эрмита будет

.

Новый интерполяционный многочлен Лагранжа находим по формуле (11):

следовательно,

(**)

6. Так как максимальная кратность узлов таблицы многочлена 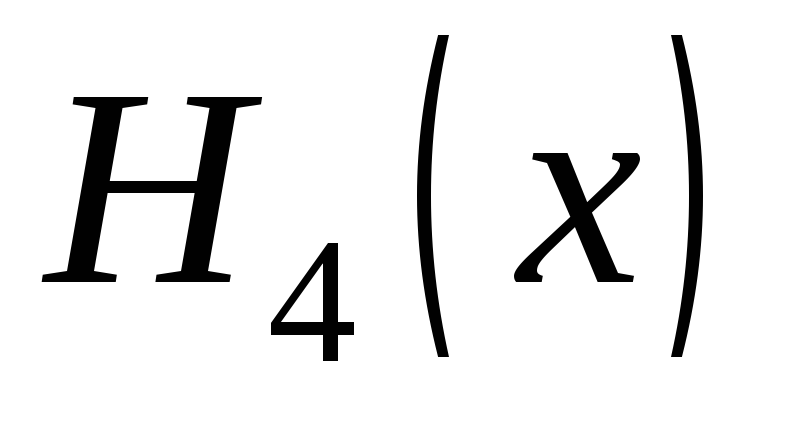равна 1, то, дифференцируя один раз уравнение (**), получаем

и по двум точкам

многочлен определяется таблицей

i	xi
0	34
1	36
2	38

восстанавливается линейной интерполяцией (10)

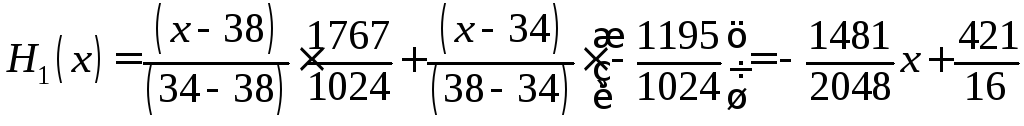
Подставляя полученное выражение в (**), получаем для искомого многочлена

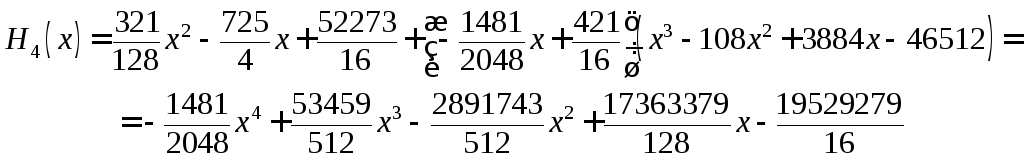
Наконец, подставляя последнее выражение в исходное (*), находим интерполирующий функцию полином Эрмита

7. Непосредственной проверкой (проверьте!), убеждаемся, что полученный многочлен действительно является интерполирующим для функции, т.е. удовлетворяет условию задачи. Кроме того, имеем возможность найти неопределенное в условии значение.