Контрольные вопросы и задачи
Дать определение истинной абсолютной и предельной абсолютной погрешностей приближенного числа. В чем их различие?
Найти предельную абсолютную погрешность числа
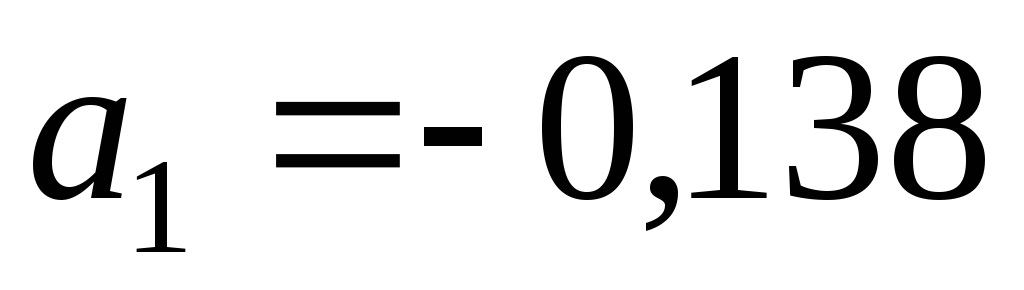числом
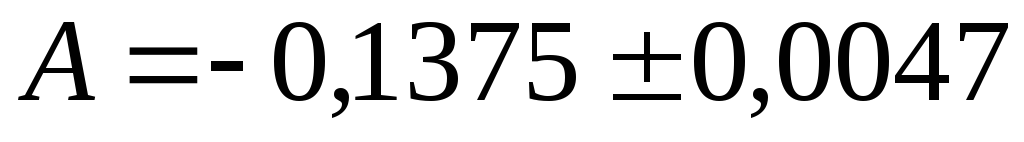.Дать определение истинной относительной и предельной относительной погрешностей приближенного числа. В чем их различие?
Вывести формулу для определения предельной относительной погрешности приближенного числа.
Найти предельную относительную погрешность числа
числом
.Выяснить, какое из приближенных равенств точнее:
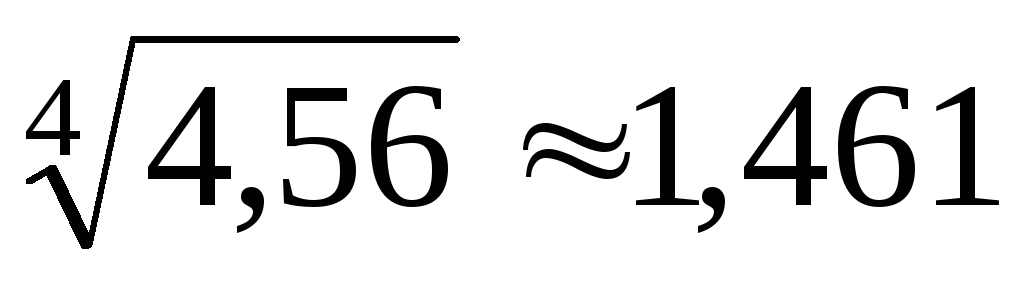или
.Дать понятие значащей, верной цифр числа.
Записать число a=104,7032 в виде позиционной записи. Найти старший и младший разряды.
В числе
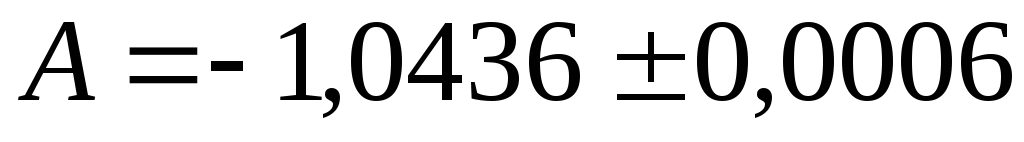найти верные цифры. Округлить приближенное
число с сохранением верных цифр.Вывести формулу для вычисления предельной абсолютной погрешности суммы (разности) двух приближенных чисел.
Даны числа
;
;
.
Найти приближение
для точного числа
.
Вычислить погрешности; результат
округлить с сохранением верных цифр.Вывести формулы для вычисления предельной абсолютной и предельной относительной погрешностей произведения (частного) двух приближенных чисел.
Чему равны
.Дано число
.
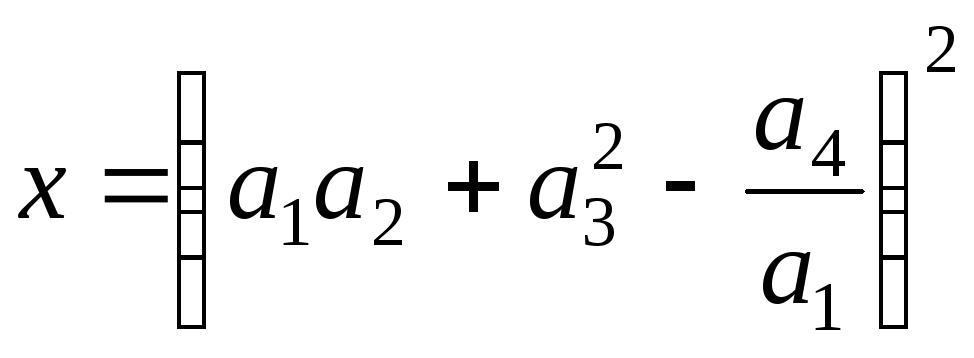Выразить
через числа
и их предельные абсолютные погрешности.Пусть
.
Выразить
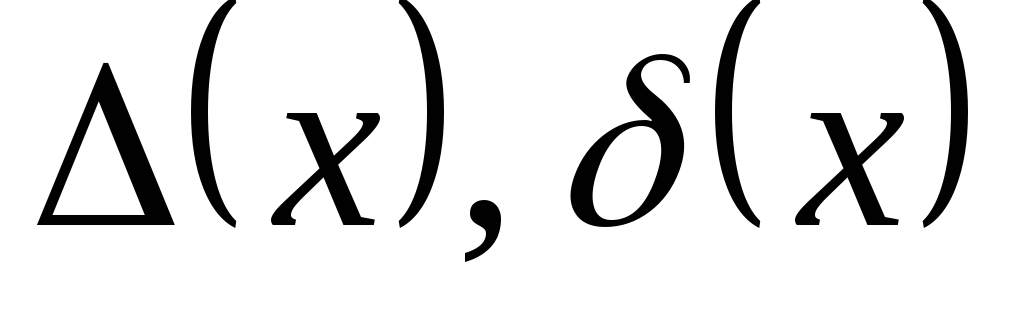через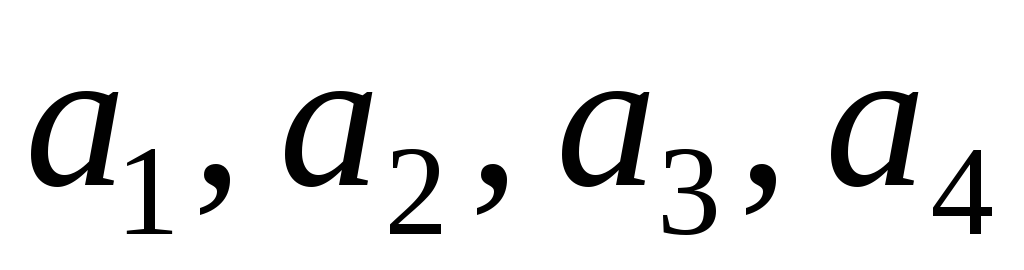
и их предельные абсолютные погрешности.Вывести формулы для вычисления предельной абсолютной и предельной относительной погрешностей значения функции в точке.
Вывести формулы для вычисления предельной абсолютной и предельной относительной погрешностей значений основных элементарных функций.
Дать алгоритм табулирования функции на заданном отрезке с заданным шагом.
19.
Построить квадратичную интерполяцию
Лагранжа, сплайн-интерполяцию и график
функции
на отрезке
по трем ее значениям:
,
,
.
Найти остаточный член, оценить погрешность
интерполяции по контрольной точке
и сравнить ее с фактической (по таблицам).
|
№ |
|
|
|
|
|
№ |
|
|
|
|
|
|
1 |
|
0 |
/2 |
|
/10 |
16 |
|
0 |
/2 |
|
/10 |
|
2 |
|
0 |
/4 |
/2 |
/10 |
17 |
|
2 |
3 |
4 |
2.5 |
|
3 |
|
1 |
10 |
100 |
15 |
18 |
|
1 |
2 |
3 |
2.5 |
|
4 |
|
0 |
/4 |
/3 |
/6 |
19 |
|
1 |
2 |
3 |
2.5 |
|
5 |
|
0 |
1/2 |
1 |
1/10 |
20 |
|
0 |
/4 |
/3 |
/6 |
|
6 |
|
0 |
1/2 |
1 |
1/10 |
21 |
|
1 |
2 |
3 |
2.5 |
|
7 |
|
1/5 |
1/3 |
2/3 |
1/4 |
22 |
|
1 |
2 |
3 |
2.5 |
|
8 |
|
1 |
10 |
100 |
78 |
23 |
|
1 |
2 |
3 |
2.5 |
|
9 |
|
0 |
/4 |
/3 |
/6 |
24 |
|
1 |
10 |
100 |
28 |
|
10 |
|
0 |
|
2 |
/8 |
25 |
|
1 |
2 |
3 |
2.5 |
|
11 |
|
0 |
/4 |
/2 |
/8 |
26 |
|
1 |
16 |
64 |
2.5 |
|
12 |
|
1 |
4 |
8 |
2.5 |
27 |
|
3 |
5 |
7 |
4.5 |
|
13 |
|
1 |
8 |
16 |
2.5 |
28 |
|
3 |
5 |
7 |
2.5 |
|
14 |
|
1 |
2 |
3 |
2.5 |
29 |
|
1 |
2 |
3 |
2.5 |
|
15 |
|
1 |
2 |
3 |
2.5 |
30 |
|
5 |
6 |
7 |
5.5 |
21. Найдите многочлен, данные о котором представлены следующей таблицей:
|
№ |
x |
|
|
|
№ |
x |
|
|
|
|
1. |
1 |
3 |
3 |
4 |
16. |
4 |
3 |
3 |
4 |
|
2 |
|
3 |
3 |
6 |
3 |
3 |
| ||
|
3 |
3 |
|
8 |
8 |
3 |
|
8 | ||
|
2 |
3 |
3 |
2 |
4 |
17 |
6 |
9 |
9 |
4 |
|
6 |
8 |
3 |
|
8 |
|
3 |
| ||
|
9 |
4 |
1 |
|
10 |
3 |
3 |
8 | ||
|
3 |
5 |
6 |
2 |
4 |
18 |
4 |
3 |
3 |
4 |
|
10 |
|
3 |
|
6 |
3 |
3 |
1 | ||
|
15 |
3 |
1 |
8 |
8 |
|
|
8 | ||
|
4 |
8 |
3 |
3 |
4 |
19 |
7 |
6 |
3 |
4 |
|
16 |
3 |
0 |
|
14 |
3 |
3 |
| ||
|
24 |
3 |
1 |
8 |
21 |
1 |
1 |
8 | ||
|
5 |
34 |
3 |
3 |
4 |
20 |
5 |
3 |
3 |
4 |
|
36 |
|
3 |
|
10 |
|
3 |
| ||
|
38 |
3 |
1 |
8 |
15 |
3 |
1 |
8 | ||
|
6 |
1 |
6 |
3 |
4 |
21 |
8 |
|
2 |
4 |
|
6 |
8 |
|
|
16 |
|
0 |
| ||
|
11 |
1 |
1 |
8 |
24 |
3 |
1 |
8 | ||
|
7 |
7 |
6 |
2 |
4 |
22 |
1 |
3 |
2 |
4 |
|
14 |
8 |
3 |
|
6 |
8 |
0 |
| ||
|
21 |
|
1 |
8 |
11 |
1 |
1 |
8 | ||
|
8 |
4 |
6 |
32 |
4 |
23 |
34 |
6 |
2 |
4 |
|
7 |
8 |
3 |
|
36 |
3 |
0 |
| ||
|
9 |
|
1 |
8 |
38 |
1 |
1 |
| ||
|
9 |
10 |
3 |
32 |
4 |
24 |
8 |
3 |
3 |
4 |
|
20 |
3 |
3 |
|
16 |
3 |
3 |
3 | ||
|
30 |
1 |
|
8 |
24 |
|
|
8 |
|
№ |
x |
|
|
|
№ |
x |
|
|
|
|
10 |
30 |
3 |
3 |
4 |
25 |
2 |
3 |
3 |
4 |
|
40 |
3 |
3 |
|
3 |
|
3 |
| ||
|
50 |
|
1 |
8 |
4 |
31 |
1 |
8 | ||
|
11 |
10 |
3 |
|
4 |
26 |
2 |
3 |
3 |
4 |
|
12 |
3 |
3 |
3 |
6 |
3 |
|
| ||
|
14 |
|
1 |
8 |
8 |
3 |
1 |
8 | ||
|
12 |
7 |
6 |
3 |
4 |
27 |
1 |
3 |
3 |
4 |
|
9 |
8 |
3 |
|
6 |
3 |
3 |
| ||
|
11 |
1 |
1 |
8 |
11 |
3 |
1 |
8 | ||
|
13 |
8 |
6 |
3 |
4 |
28 |
1 |
3 |
3 |
4 |
|
12 |
8 |
3 |
|
2 |
3 |
3 |
| ||
|
16 |
1 |
|
8 |
3 |
1 |
1 |
8 | ||
|
14 |
34 |
6 |
3 |
|
29 |
3 |
6 |
3 |
4 |
|
36 |
|
3 |
38 |
9 |
8 |
3 |
| ||
|
38 |
1 |
1 |
8 |
15 |
1 |
1 |
8 | ||
|
15 |
7 |
6 |
3 |
4 |
30 |
4 |
6 |
3 |
4 |
|
8 |
|
3 |
38 |
6 |
3 |
3 |
31 | ||
|
9 |
1 |
|
8 |
8 |
|
|
8 |
