
ChM_V_INZhENERNYKh_RASChYoTAKh_chast_1
.pdf
еѐ к векторам в (3.4) и записать |
x * x(k 1) |
и |
|
C(x * x( k ) ) |
|
, то урав- |
нение в (3.4) приобретѐт скалярный вид и сходство в строке (3.3) усилится.
Обобщая длину вектора как меру сразу всех его компонент, записывают норму 
 x
x
 вектора в виде:
вектора в виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
|
|
|
|
|
|
|
|
p 1 p . |
|
|||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
p |
p |
|
|
x1 |
|
p |
|
xn |
|
p |
p |
|
xn |
(3.5) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
Практически используют нормы при p, равном 1, 2 и , то есть: |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
max |
|
|
|
|
|
||||||||||||||||||
|
|
x |
|
|
|
xi |
|
; |
|
|
x |
|
|
|
|
|
|
x |
|
x12 |
xn |
2 ; |
|
x |
|
|
|
|
xi |
|
. |
(3.6) |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|||
Рассматривая вместо |
Cx вектор |
Ce с произвольным единичным |
||||||||||||||||||||||||||||||||||||||||||||||||||||
вектором e , вводят матричную норму 
 C
C
 , подчинѐнную соответствующей векторной норме, как
, подчинѐнную соответствующей векторной норме, как
C |
|
|
|
|
|
|
|
C |
|
p |
max |
|
|
|
Ce |
|
|
|
p . |
(3.7) |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
|
|
Она характеризует наибольшее растяжение вектора при умножении на C . Для итерационной формулы в (3.4) с учѐтом (4.7) можно записать:
x* x(k 1) |
|
|
|
C(x* x(k ) ) |
|
|
|
C |
|
|
|
(x* x(k ) ) |
|
. |
(3.8) |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из (3.8) по аналогии с условием c 1 можно заключить, что
для сходимости метода простых итераций при любом x(0) достаточно, чтобы матричная норма была бы меньше 1, то есть 
 C
C
 1.
1.
Матричные нормы вычисляются по формулам:
|
|
|
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
C |
|
1 maxj |
i 1 |
ci, j |
; |
|
C |
|
maxi |
j 1 |
ci, j |
. |
(3.9) |
|
|
|
|
|
|
|
|
|
|
Вторая норма матрицы, равная арифметическому корню из наибольшего собственного значения матрицы CTC , трудно вычисляема и для практической оценки сходимости не применяется. По аналогии с методом итераций для одного уравнения можно записать формулу для
51
завершения итераций, гарантирующих абсолютную погрешность при
достижении x(k 1) |
не больше, чем : |
|
|
|||||||||||||||||
|
|
x(k 1) x(k ) |
|
|
1 |
|
|
|
|
|
Delta . |
(3.10) |
||||||||
|
|
|
|
C |
|
|
||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
C |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|||||
Для бесконечной нормы |
|
|
|
с величиной Delta |
сравнивают наи- |
|||||||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
большую из разностей между компонентами x для итераций (k+1) и (k). По назначенной в расчѐтах величине Delta оценку гарантированной точности полученного решения можно определить по этой же формуле.
Достаточное условие сходимости (его называют диагональным преобладанием) сформулируем для специальной схемы получения итерационной формулы, использованной в численном примере.
Для сходимости метода простых итераций при решении СЛАУ Ax=b при любом начальном приближении x(0) достаточно, чтобы:
или абсолютная величина элемента на главной диагонали для любого столбца матрицы была больше суммы абсолютных величин всех дру-
|
|
n |
|
, j 1, , n , |
|
|
|
||
гих элементов этого столбца, то есть |
aj, j |
i 1 |
ai, j |
|
|
|
i j |
|
|
или абсолютная величина элемента на главной диагонали для любой строки матрицы была больше суммы абсолютных величин всех дру-
|
|
n |
|
|
, i 1, , n . |
|
|
|
|
||
гих элементов этой строки, то есть |
ai,i |
j 1 |
ai, j |
||
|
|
j |
i |
|
|
Заметим, что это достаточное условие – его выполнение гарантирует сходимость, но если оно не выполнено, то итерации могут как сходиться, так и расходиться. Например, для рассмотренного числового
|
|
|
|
|
|
|
|
|
|
|
|
|
5 2 3 |
|
a2,1 |
|
|
|
a2,3 |
|
, или для 2-го |
|
примера, |
|
для 2-ой строки: |
a2,2 |
|
|
|
|
|||||||||||||||
столбца |
|
a2,2 |
|
5 4 3 |
|
a1,2 |
|
|
|
a3,2 |
|
, |
а расчѐты показывают сходимость. |
|||||||||
|
|
|
|
|
|
|||||||||||||||||
Необходимые и достаточные условия требуют, чтобы все собственные значения матрицы C были по абсолютной величине меньше 1.
52

3.1.3 Метод Зейделя
Для рассмотренной в разделе 3 системы уравнений (I, II, III) выразим неизвестные, расположенные на главной диагонали,
|
2x1 |
1x2 |
1x3 |
|
1 |
(I) |
||
|
4x1 |
3x2 |
|
0x3 |
|
2 |
(II) |
|
|
|
|
||||||
2x |
2x |
2 |
3x |
3 |
9 |
(III) |
||
|
1 |
|
|
|
|
|||
x(k 1)
x(k 1)
2
x3(k 1)1
0x1(k ) 1x2(k ) 1x3(k )
4x1(k 1) 0x3(k ) 0x3(k )
2x1(k 1) 2x2(k 1) 0x3(k )
2 1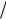 2
2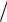 3 2
3 2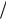 3
3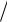 3 9
3 9 3
3
То есть, применим такую же специальную схему преобразования системы, как и в методе простых итераций, однако, вычисляемые компоненты неизвестных здесь сразу используем в последующих уравнениях – на это указывают номера итераций (k+1) компонент, расположенных правее знаков равенства. В этом и состоит характерное отличие стационарного метода Зейделя, называемого ещѐ методом Зей-
деля-Гаусса.
Таким же образом (как в методе простых итераций) выберем век-
тор |
x(0) |
начального приближения, |
например, |
x(0) |
1 2 |
2 3 9 3 T |
||||||||
0.5 0.67 |
3 T , и найдѐм последующие приближения: |
|
|
|
|
|
|
|||||||
|
x1(1) 0x1(0) 1 0.67 1 3 2 0.5 1.33 |
|
|
|
0.96 |
|
|
1.00 |
||||||
x(1) |
4 ( 1.33) 0x(0) 1 2.5 3 0.67 2.44 |
, |
x(2) |
|
1.95 |
|
, |
x(3) |
|
2.01 |
|
|||
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
||
x(1) |
2 ( 1.33) 2 2.44 0 x(0) 3 3 0.48 |
|
|
|
1.06 |
|
|
|
|
0.99 |
|
|||
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
Последовательность векторов x(k ) |
быстро |
сходится |
к |
решению |
||||||||||
x* 1 2 1 T . |
|
|
|
|
|
|
|
|
|
|
|
|||
Метод Зейделя во многом похож на метод простых итераций, для обоих методов справедливо сформулированное выше достаточное условие сходимости (для метода Зейделя допустимы не строгие неравенства и хотя бы одно строгое). Структура формулы (см. [1]) для завершения итераций при выполненном достаточном условии подобна
(3.10).
|
x(k 1) x(k ) |
|
|
1 |
Delta , |
(3.11) |
|
|
|||||
|
|
|
||||
|
|
|
|
|
|
но в качестве можно использовать вместо 
 C
C
 величину
величину
53
|
|
|
n |
|
|
ci, j |
|
|
|
|
|
n |
|
ai, j |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
max |
|
|
j i |
|
|
|
|
|
max |
|
|
j i 1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
i 1 |
|
|
|
или |
|
|
|
i 1 |
|
|
, |
(3.12) |
||||||
i |
1 |
|
ci, j |
|
i |
ai,i |
ai, j |
||||||||||||||
|
|
j 1 |
|
|
|
|
|
j 1 |
|
|
|
||||||||||
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
где формула, указанная слева, относится к преобразованной системе общего вида (3.1), а справа - к специальной схеме преобразования исходной системы.
Однако метод Зейделя и метод простых итераций имеют свои не одинаковые необходимые и достаточные условия сходимости. Поэтому можно привести примеры, для которых один из методов сходится, а другой нет. По условиям сходимости методов можно сказать, что для матриц СЛАУ с диагональным преобладание хорошо сходится метод простых итераций, а для быстрой сходимости метода Зейделя матрица должна быть близка к нижней треугольной. Заметим, что для строго нижней треугольной матрицы метод Зейделя даѐт решение после первой «итерации». Отметим, что нормализация системы (см. в разделах 3.2 и 5) делает еѐ теоретически сходящейся по методу Зейделя.
3.1.4 О применении итерационных методов
Для систем линейных уравнений с плотно заполненной матрицей итерационные методы не имеют преимуществ перед прямыми методами. Модификации прямых методов хорошо работают и с ленточными положительно-определѐнными матрицами (они часто встречаются в технических расчѐтах) – при решении ширина ленты не увеличивается и не занимает дополнительной памяти. Но для систем уравнений с редко заполненными матрицами больших размеров прямые методы, которые в процессе решения заполняют числами прежде «нулевые» элементы матрицы, требуют огромные объѐмы памяти. А вот итерационные методы не изменяют коэффициенты в матрице системы в процессе вычислений. Более того, для многих СЛАУ, встречающихся в приложениях, коэффициенты в уравнениях составляют небольшие наборы чисел, например, числа: 4; 2;-1, которые вообще не нужно хранить в матрице – они просто записываются в операторах расчѐтной программы. Если коэффициенты легко вычисля-
54
ются, то также можно обойтись без матрицы. Для таких СЛАУ итерационные методы весьма эффективны. Заметим, что при хорошей сходимости (о чѐм в итерационных методах приходится особо заботиться) требуется мало итераций для получения результата с небольшой инженерной точностью – это сокращает время решения задачи.
Отметим, что в пакетах для математических расчѐтов нет универсальной подпрограммы для эффективного решения СЛАУ итерационными методами. Отдельные программы тесно связаны со спецификой своих задач и успешно решают только их. Поэтому обычно программируют итерационное решение СЛАУ, ориентируясь на особенности структуры матрицы коэффициентов своей конкретной системы.
3.2 Задание к расчетно-графической работе №3
Задание 1. Решить СЛАУ из раздела 2.3.2 методом Зейделя; для этого:
a.Проверить и, при необходимости, обеспечить сходимость мето-
да. (Для обеспечения сходимости возможно потребуется преобразовать Ax b Hx f систему: Ax b к сходящейся Hx f . см. далее «Способы приведения исходной СЛАУ…»).
b. Вычислить вектор начального приближения для системы H x f ,
у которой обеспечивается условие сходимости. Рекомендуется |
|
этот вектор вычисляется по формуле: x(0) f1 / h1,1 f2 / h2,2 |
f3 / h3,3 T . |
c. Привести систему Hx f к итерационной форме, |
выразив xi |
из i -го уравнения (для всех уравнений). Затем, используя вектор начального приближения x0 , выполнить по методу Зейделя необходимое число итераций для получения совпадения 2-ой после запятой значащей цифры во всех компонентах вектора решения.
Представить в отчѐте СЛАУ Ax b; Hx f с пояснением выполненного преобразования, программу расчета и результаты двух первых ( x(0) , x(1) ) и последнего приближений.
55
Задание 2. Решить СЛАУ (см. далее «Варианты задания 2») методом итераций или методом Зейделя. Компоненты вектора решения вычислять с абсолютной погрешностью не более 0.001.
3.2.1 Пример выполнения задания 1
а. Сходимость метода Зейделя гарантируется при выполнении како- го-либо условия, например, диагонального преобладания (способ 1) или преобладания нижней левой треугольной части матрицы (способ 2), нормализация системы также достаточна для теоретической сходимости метода (способ 3). Далее на примерах поясняются эти способы приведения Ax b к Hx f и проверки условий сходимости метода для системы Hx f .
Отметим, что при приведении исходной системы Ax b к схо-
дящейся Hx f по способам 1 и 2 используют равносильные преобразования системы: складывают, вычитают, переставляют уравнения, предварительно умножают их на ненулевые коэффициенты; переставляют столбцы матрицы системы (т.е. меняют порядок неизвестных) и стремятся получить диагональное преобладание или (по способу 2) большие по абсолютной величине числа в нижней треугольной части матрицы. В способе 2 целесообразно проверить реализованное для системы из трѐх уравнений необходимое и достаточное условие сходимости метода Зейделя. При этом вычисляются коэффи-
циенты , 1 , 2 , 3 , |
4 , , , и для 2 |
4 убеждаются, что 2 4 2 и |
||
sign (α) (α γ) |β | , |
а при 2 4 |
сходимость |
имеет место при |
|
sign( ) ( ) 0 . Нормализация системы Ax b |
, которая заключа- |
|||
ется в умножении правой и левой еѐ частей на матрицу AT |
, теоре- |
|||
тически гарантирует сходимость, но она может оказаться очень медленной.
56

Способы приведения исходной СЛАУ к сходящейся (по методу Зейделя) (Способ 1) Получение диагонального преобладания: Сходящиеся системы
перестановкой строк
(i) 2 |
4 |
1 |
x1 |
|
|
7 |
(iii) 7 |
4 |
2 |
x2 |
|
1 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ii) |
1 |
3 |
5 |
x2 |
|
|
0 |
|
(ii) |
1 |
3 |
5 x1 |
|
|
0 |
|
|
|
7 |
4 |
2 |
|
|
|
1 |
|
|
2 |
4 |
1 |
|
|
|
7 |
|
(iii ) |
x2 |
|
|
|
(i) |
x3 |
|
|
|
||||||||
перестановкой столбцов
(i) |
2 |
4 |
1 |
x1 |
|
7 |
|
|
(i) 4 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(ii) |
|
1 |
3 |
5 |
|
x2 |
|
0 |
|
|
(i) |
|
3 |
|
|
7 |
4 |
2 |
|
|
|
|
|
|
|
|
4 |
(iii) |
|
x3 |
|
1 |
|
|
(iii) |
||||||
|
( j) |
( jj) |
( jjj) |
|
|
|
|
|
|
( jj) |
|||
(Способ 2)
Преобладание нижней левой треугольной части матрицы
2 |
1 |
|
x1 |
|
|
7 |
|
|
|
|
|
|
|
|
|
1 |
5 |
|
x2 |
|
|
0 |
|
7 |
2 |
|
|
|
|
|
|
|
x3 |
|
1 |
|
|||
( j) |
( jjj) |
|
|
|
|
|
|
(ii ' ) (ii) 2 (iii)
|
(i) [ 4] 2 |
1 |
x1 |
|
7 |
|
||
|
|
|
|
|
|
|
|
|
(ii) |
3 |
[5] |
1 |
x2 |
|
0 |
|
|
|
|
4 |
2 |
|
|
|
|
|
|
(iii ) |
[ 7] x3 |
|
1 |
|
|||
|
|
( jj) |
( jjj) |
( j) |
|
|
|
|
|
(i) |
5 1 |
3 |
x1 |
|
1 |
|
|
|
(i ' ) (i) (ii) (iii) |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
(ii) |
4 |
3 |
2 |
x |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
1 |
|
|
2 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(iii) |
3 |
5 |
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
Проверка необходимого и |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
достаточного условия сходимости: |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
( 4) ( 3) 5 60 , ( 1) 2 3 6, 4 0 4 ( 1) 0 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 0 ( 3) 3 0, 2 ( 4) 2 ( 1) 8, 3 ( 1) 4 5 20 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 4 |
(0) 8 ( 20) 0 12 |
|||||||||||||
|
Случай 4 2 |
|
|
|
4 60 ( 6) |
(12)2 . |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
sign (α) (α γ) |β | |
|
|
|
При этом: |
|
|
2 4 2 |
(12)2 4 602 |
|
- |
верно ! |
||||||||||||||||
|
и |
|
знак(60) (60 ( 6)) |12 | |
1 (54) 12 |
- |
верно ! |
||||||||||||||||||||||||
|
Для случая 2 4 |
сходимость будет при |
sign( ) ( ) 0 . |
|
||||||||||||||||||||||||||
|
(Способ 3) Умножение (слева) системы на транспонированную матрицу |
|||||||||||||||||||||||||||||
|
|
|
|
AT |
|
|
|
A x |
|
AT f |
|
|
|
|
|
|
H |
x f |
|
|||||||||||
|
5 4 |
3 |
5 1 |
|
3 |
|
x1 |
|
|
5 4 |
3 |
|
1 |
|
|
50 |
20 |
8 |
x1 |
|
2 |
|||||||||
|
1 |
3 |
1 |
4 |
|
3 2 |
|
x2 |
|
|
1 |
3 |
1 |
|
|
3 |
|
20 11 |
8 |
x |
|
|
|
5 |
|
|||||
|
3 2 |
|
3 |
1 5 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
8 |
|
|
2 |
|
|
|
|
|||||
|
5 |
|
x3 |
|
2 5 |
|
5 |
|
8 |
38 |
x |
3 |
|
|
22 |
|
||||||||||||||
50 ( 5) ( 5) 4 4 3 3 ; |
|
|
20 1 ( 5) ( 3) 4 ( 1) 3 ; |
8 3 ( 5) 2 4 5 3 |
||||||||||||||||||||||||||
11 1 1 ( 3) ( 3) ( 1) ( 1) ; |
8 3 1 2 ( 3) 5 ( 1) ; |
38 3 3 2 2 5 5 |
||||||||||||||||||||||||||||
2 ( 5) 1 4 ( 3) 3 5 |
|
5 1 1 ( 3) ( 3) ( 1) 5 |
22 3 1 2 ( 3) 5 5 |
|||||||||||||||||||||||||||
57

Поверим необходимое о достаточное условие для системы H x f
|
2x1 |
1x2 |
1x3 |
1 |
(I) |
|
Таблица 3.1 |
|
|
|
|
|
|
||||||||
|
4x1 |
3x2 |
|
0x3 2 |
(II) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
H |
|
|
|
|
H |
|
|||||||||||
2x |
2x |
|
3x |
|
9 |
(III) |
|
|
|
|
|
|
|
|
|||||||
2 |
3 |
|
2 |
|
1 |
|
|
1 |
2 |
|
|
1 |
1 |
||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||
По таблице 3.1 |
со сдвоенной |
4 |
|
3 |
|
|
0 |
4 |
|
|
3 |
0 |
|||||||||
-2 |
|
2 |
|
|
3 |
-2 |
|
|
2 |
3 |
|||||||||||
матрицей H системы вычисля- |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
ем коэффициенты: 18; 1 6; 2 0; 3 |
12; 4 |
8; ( 6) 0 12 8 2 . |
|||||||||||||||||||
Поскольку 2 |
4 22 |
4 18 0 , то для этого случая проверяем усло- |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
вия: 2 4 2 22 |
4 182 |
и sign ( ) ( ) |
|
|
|
1 (18 0) |
2 |
. |
|
||||||||||||
Оба условия выполняются, следовательно, система H x f |
|
будет да- |
|||||||||||||||||||
вать сходящийся процесс, задаваемый итерационной формулой (см. пункт c.).
b. В соответствии с рекомендацией x(0) 1 2 2 3 9 3 T 0.5 0.67 |
3 T . |
||||
c. Приводим систему H |
x f к итерационной форме: |
|
|||
x(k 1) |
0x(k ) |
1x(k ) |
1x(k ) 2 1 2 |
|
|
|
1 |
1 |
2 |
3 |
|
|
4x1(k 1) 0x3(k ) 0x3(k ) 3 2 3 |
|
|||
x2(k 1) |
|
||||
x(k 1) |
2x(k 1) 2x(k 1) |
0x(k ) 3 9 3 |
|
||
|
3 |
1 |
2 |
3 |
|
Для вычисления приближений по методу Зейделя используем макрос:
Sub Пример_4_1()
k = 0: x1 = 1 / 2: x2 = 2 / 3: x3 = 9 / 3
Cells(k + 2, 1) = k: Cells(k + 2, 2) = x1: Cells(k + 2, 3) = x2: Cells(k + 2, 4) = x3
Do
w = (1 - 1 * x2 - 1 * x3) / 2: Delta = Abs(w - x1): x1 = w
w = (2 - 4 * x1) / 3: v = Abs(w - x2): Delta = IIf(v > Delta, v, Delta): x2 = w w= (9+2 * x1 - 2 * x2) /3: v = Abs(w - x3): Delta = IIf(V > Delta, v, Delta): x3= w k = k + 1
Cells(k + 2, 1) = k: Cells(k + 2, 2) = x1: Cells(k + 2, 3) = x2: Cells(k + 2, 4) = x3 Loop While Abs(Delta) > 0.001
End Sub
Результаты решения представлены в таблице 3.2.
58
Таблица 3.2
|
A |
B |
C |
D |
1 |
k |
x1 |
x2 |
x3 |
2 |
0 |
0,5 |
0,666667 |
3 |
3 |
1 |
-1,33333 |
2,444444 |
0,481481 |
4 |
2 |
-0,96296 |
1,950617 |
1,057613 |
5 |
3 |
-1,00412 |
2,005487 |
0,993599 |
6 |
4 |
-0,99954 |
1,99939 |
1,000711 |
7 |
5 |
-1,00005 |
2,000068 |
0,999921 |
|
|
|
|
|
|
n o o 3 o o o o o o |
|
|
n |
|
|
|
|
|
|
|
|
o n o o 3 o o |
o o o |
|
5 |
||
o o n o o 3 o |
o o o |
|
5 |
||
|
|
|
|
|
|
2 o o n o o 3 |
o o o |
|
5 |
||
|
|
|
|
|
|
1 4 o o n o o |
3 o o |
|
5 |
||
A |
|
|
,b |
|
|
o 1 2 o o n o |
o 3 o |
|
5 |
||
|
|
|
|
|
|
o o 1 4 o o n |
o o 3 |
|
5 |
||
o o o 1 2 o o |
n o o |
|
5 |
||
|
|
|
|
|
|
o o o o 1 4 o |
o n o |
5 |
|||
o o o o o 1 2o |
o o n |
n |
|||
Рисунок 3.1
3.2.2 Пример выполнения задания 2
Sub Пример_3_2() ʹ См. рисунок 3.1, n=9 Dim x(1 To 10) As Double, y(1 To 10) As Double Dim b(1 To 10) As Double, S As Double
n=9: For i = 1 To 10: b(i) = 5: x(i) = b(i) / n: Next i
b(1) = n: b(10) = n: x(1) = 1: x(10) = 1 k = 0: Cells(k + 2, 1) = k
For i = 1 To 10: Cells(k + 2, i + 1) = x(i): Next i Do: k = k + 1
For i = 1 To 10 S = b(i):
j = i + 3: If j < 11 Then S = S - 3 * x(j)
j = i - 3: If 0 < j Then S = S - IIf(i Mod 2, 4, 2) * x(j) j = i - 4: If 0 < j Then S = S - 1 * x(j)
y(i) = S / n
Next i
Cells(k + 2, i) = k: Delta = 0: For i = 1 To 10:
S = Abs(y(i) - x(i)): If S > Delta Then Delta = S x(i) = y(i): Cells(k + 2, i + 1) = x(i)
Next i
Loop While Delta > 0.0001
End Sub
59
Вектор решения, вычисленный по программе, приведѐн в таблице 3.3.
Таблица 3.3
k |
X(1) |
X(2) |
X(3) |
X4) |
X(5) |
X6) |
X(7) |
X(8) |
X(9) |
X(10) |
16 |
0,8829 |
0,5391 |
0,4746 |
0,3513 |
0,0493 |
0,2428 |
0,0242 |
0,5056 |
0,4422 |
0,9677 |
3.2.3 Варианты задания 1
см. в разделе 2.3.2
3.2.4 Варианты задания 2
Вар. n=1-5
2n
ooo1
A o
o
oooo
Варианты задания 2
o |
o o 1 |
o |
o o o o |
|
|
n |
|
|||||
2n o |
o o 1 |
o |
o o o |
|
|
|
|
|||||
|
|
n |
|
|||||||||
o |
2n o o o 1 |
o |
o o |
|
|
n |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
o o |
2n o o o 1 |
o |
o |
|
|
n |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
o |
o o |
2n o |
o o 1 |
o |
|
|
2 |
|||||
|
|
|
|
|
|
|
|
|
|
, |
b |
|
1 |
o |
o o |
2n o o o 1 |
|
|
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
o 1 |
o |
o o |
2n o o o |
|
|
n |
|
|||||
o o 1 |
o |
o o |
2n o o |
|
|
n |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
o o o 1 |
o |
o o |
2n o |
|
|
n |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
o o o o 1 |
o o o |
2n |
|
n |
|
|||||||
Вар. n=6-10
n
oo21
A o
oooo
Варианты задания 2
o o 2 1 o o o o |
o |
|
n |
|
||
n o o 2 1 o |
o o |
o |
|
|
|
|
|
|
n |
|
|||
o n o o 2 1 o o |
o |
|
|
n |
|
|
|
|
|
|
|
|
|
o o n o o 2 1 o |
o |
|
|
n |
|
|
|
|
|
|
|
|
|
2 o o n o o 2 1 |
o |
|
|
2 |
||
|
|
|
|
, |
b |
|
1 2 o o n o o 2 1 |
|
|
2 |
|||
|
|
|
|
|
|
|
o 1 2 o o n o o 2 |
|
|
n |
|
||
o o 1 2 o o n o |
o |
|
|
n |
|
|
|
|
|
|
|
|
|
o o o 1 2 o o n |
o |
|
|
n |
|
|
|
|
|
|
|
|
|
o o o o 1 2 o o n |
|
6 |
||||
60
