
ChM_V_INZhENERNYKh_RASChYoTAKh_chast_1
.pdf1 РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1 Решение нелинейных уравнений
1.1Краткие теоретические сведения
Нелинейным называется уравнение вида
f (x) 0, |
(1.1) |
если его левая часть не является линейной функцией. Функция f(x) может содержать трансцендентные, специальные функции или сте-
пень неизвестного x . |
Квадратное |
алгебраическое уравнение |
ax 2 bx c 0 является |
нелинейным |
уравнением, корни которого |
можно определить по прямым формулам. Аналитические решения существуют также для корней полиномиальных уравнений, степень которых, согласно теореме Н.Абеля (30-е года XIX века), не выше четвертой. В инженерной практике обычно приходится решать нелинейные уравнения более сложного вида, вычислить значения корней которых в виде конечной формулы оказывается невозможным.
Корень уравнения f (x) 0 называется простым, если′ ( ) ≠ 0. В противном случае (т.е. если ′ =0) корень называется кратным. Геометрически корень уравнения соответствует абсциссе точки пересечения графика функции y f (x) с осью Ox. Корень является простым, если график функции пересекает ось Ox под ненулевым углом, и кратным, если пересечение происходит под нулевым углом. Функция f(x) представленная на рисунке 1.1 имеет
пять корней: три простых корня 1 , 2 и 3, и два кратных корня 4 и
5 .
Задача отыскания простых корней является более простой (и чаще встречающейся), чем задача определения кратных корней. Рассматриваемые в данной работе методы поиска корней нелинейных уравнений ориентированы, в первую очередь, на отыскание простых корней.
11

y
|
|
2. |
|
3. |
|
|
|
5 |
|
|
|
|
|
||||
1. |
|
|
|
|
|
4. |
|
|
|
|
|
|
|
|
x
Рисунок 1.1 – График нелинейной функции с пятью корнями
Решение задачи отыскания корней нелинейного уравнения осуществляется в два этапа. Первый этап называется этапом локализа-
ции (или отделения корней), второй – этапом итерационного уточнения корней.
Первый этап. Локализация корней. Отрезок [a,b], содержащий только один корень уравнения (1.1), называют отрезком локализации корня . Цель этапа локализации считается достигнутой, если для каждого из подлежащих определению корней удалось указать отрезок локализации. Длину отрезка локализации стремятся сделать минимальной. Указать универсальный метод локализации корней не представляется возможным. Наиболее часто используют: построение графика функции f(x) и табличный способ отделения корней.
Наличие персонального компьютера с пакетом MS Office позволяет, достаточно легко, построить график нелинейной функции, анализ которой позволит определить отрезки локализации. Напомним, что удобнее всего для построения графика функции одной переменной использовать точечную диаграмму Excel. В некоторых случаях, когда функцию f(x) можно разложить на две функции f1(x) и f2(x) простого вида, использование компьютера может не потребоваться. Например, уравнение − − = 0 можно преобразовать к виду = − и, построив графики двух функций 1 = и 2 = − ( см. рисунок 1.2), можно определить отрезок локализации корня ([0:1]) без выполнения расчетов на ЭВМ.
12

|
y |
|
|
|
|
|
2 |
|
|
|
|
|
1 |
= |
|
|
|
|
1 |
|
|
|
|
|
|
|
= − |
|
|
|
|
2 |
|
|
|
|
0 |
|
|
|
|
-1 |
|
1 |
2 |
x |
|
Рисунок 1.2 – Графики функций |
= и |
= − |
|||
|
|
1 |
|
2 |
|
Применение табличного способа локализации корней позволяет не использовать возможности вычислительной техники, т. к. не требует точного вычисления значений функций. Значение функции требуется определить с точностью «до знака» (плюс или минус), и такие расчеты могут быть сделаны в уме. При этом способе локализации о наличии на отрезке [xi ; xi+1] корня судят по перемене знака функции на концах отрезка. Пример применения табличного способа показан на рисунке 1.3.
х |
− |
|
3 |
|
− |
− |
|
|
0 |
|
|
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
||
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
знак f(x) |
|
+ |
|
+ |
|
|
|
|
|
+ |
|
+ |
|
+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рисунок 1.3 – Иллюстрация табличного способа отделения корней
Очевидно, что в примере, представленном на рисунке 1.3, функция f(x) имеет два корня. Один корень находится в интервале [− , − 2], второй в интервале от нуля до + 2 .
К сожалению, четный корень не удается локализовать на основании перемены знака функции с помощью даже очень точной таблицы.
13
Необходимо отметить, что не всегда для успешного отыскания корня уравнения (1.1) необходимо полное решение задачи локализации. В некоторых случаях достаточно найти хорошее начальное приближение (0) к корню .
Второй этап. Итерационное уточнение корней. На этом этапе для вычисления с необходимой точностью >0 каждого из корней уравнения используют тот или другой итерационный метод, позволяющий рассчитать последовательность x(0), x(1), … , x(n) приближений к корню . Существует большое число методов для итерационного поиски корня нелинейного уравнения. В данной работе рассматриваются три наиболее часто используемых в инженерной практике (в скобках приведены названия, под которыми эти методов могут встретиться в других источниках):
метод простых итераций (метод последовательных приближений);
метод Ньютона (метод касательных);
метод деления отрезка пополам.
Уточнение корней с помощью итерационных методов связано с обеспечением (метод итераций) или проверкой (метод Ньютона) условия сходимости процесса и с выполнением определенных ограничений на гладкость функций в интервале значений аргумента, где имеется единственный корень уравнения. Как правило, эти обстоятельства налагают требования на ширину локализованного участка для корня и на характер поведения функции f (x) , еѐ первой и второй производных ( f (x) и f (x) ) на этом участке.
Метод деления отрезка пополам позволяет вычислить единственный корень уравнения с заданной точностью на интервале без наложения дополнительных условий на функцию и еѐ производные, предполагая только непрерывность функции f(x). Однако, количество арифметических операций для вычисления корня с такой же точностью что и в других рассматриваемых методах существенно больше.
14
1.2 Метод простых итераций
Для реализации метода простых итераций решения нелинейного уравнения (1.1), необходимо преобразовать это уравнение к виду:
x (x) |
(1.2) |
Это преобразование можно выполнить различными способами. Например, можно левую часть исходного уравнения (1.1) умножить на постоянный множитель отличный от нуля. а затем добавить x в обе части уравнения. В результате получается уравнение:
x x f (x) |
(1.3) |
Функция φ в этом случае будет определяться зависимостью
(x) x f (x)
Вычисление корня выполняется по следующей схеме. В отрезке локализации корня [a,b] выбирается начальное приближение x(0) и подставляется в правую часть уравнения (1.2). Получается первое приближение к корню x(1) = φ(x(0)). Подставив первое приближение x(1) в правую часть уравнения (1.2) вычисляем следующее приближение x(2) = φ(x(1)). Продолжая этот процесс неограниченно, получим последовательность приближений к корню вычисляемых по формуле
x(n+1) = φ(x(n)), n≥0 |
(1.4) |
Геометрическая интерпретация итерационного процесса метода простых итераций, для функции φ(x) с положительной первой производной, приведена на рисунке 1.4. Корнем является абсцисса точки пересечения графиков двух функций y1=x и y2=φ(x).
15

Y |
|
|
y1=x |
|
|
|
|
|
|
x(2)=φ(x(1)) |
|
|
|
y2=φ(x) |
|
|
|
|
|
x(1)=φ(x(0)) |
|
|
|
|
0 |
x(0) |
x(1) |
x |
X |
|
|
|
|
Рисунок 1.4 – Определение корня методом простой итерации
Сходимость метода итераций. Сходимость метода простых итераций связана с выполнением на отрезке локализации корня условия
|
(1.5) |
(x) 1 |
т.е. 1 (x) 1
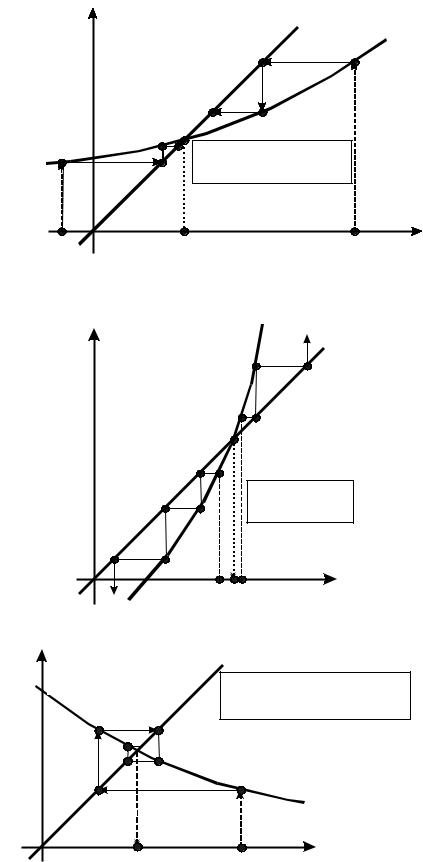
На рисунках 1.5 – 1.8 представлена геометрическая иллюстрация поведения итерационного процесса в четырех простейших случаях взаимного расположения прямой y1=x и нелинейной функции y2=φ(x). В случаях, представленных на рисунках 1.5 и 1.7, итерационный процесс сходится к корню уравнения, в случаях показанных 1.6 и 1.8 процесс расходится. Эта иллюстрация наглядно демонстрирует условие сходимости метода простых итераций выраженное формулой (1.5). Знак первой производной функции φ(x) определяет характер приближений к корню. Для положительной первой производной процесс решения происходит «ступеньками», а для отрицательной производной ′ – по спирали. Вопрос сходимости итерационного процесса при этом, определяет значение модуля первой производной итерационной функции.
16
|
y |
|
|
|
|
|
|
|
|
|
( 0 ) |
|
|
|
|
|
2 |
( 0 |
) |
|
|
|
|
1 |
|
|
|
|
|
|
|
< ′ |
< 1 |
|
|
0 |
0 |
|
|
0 |
x |
1 |
|
|
|
2 |
|
Рисунок 1.5 – При 0<φ’ x)<1 метод итераций сходится |
|||||
|
y |
|
|
|
|
|
|
( 0 |
) |
|
|
|
|
2 |
|
|
|
|
|
|
( |
0 ) |
|
|
|
|
1 |
|
|
|
|
|
φ'(x)>1 |
|
|
|
|
0 |
0 |
|
|
|
|
2 |
|
|
|
|
|
1 |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
Рисунок 1.6 – При φ’ x)>1 метод итераций расходится |
|||||
y |
− < ′ |
|
|
|
|
|
< 0 |
||
|
( 0 |
) |
|
|
|
1 |
|
|
|
|
10 |
x |
|
|
Рисунок 1.7 - При -1<φ’ x)<0 метод итераций сходится
17

y |
|
|
φ'(x)<-1 |
0 |
|
1 |
x |
Рисунок 1.8 - При φ’ x)<-1 метод итераций расходится
Из приведенных рисунков видно, что процесс итераций сходится к искомому корню, если на участке, внутри которого имеется единственный корень, выполняется условие: 1 (x) 1.
При использовании преобразования исходного уравнения (1.1) к виду (1.3), с помощью введенного множителя можно обеспечить сходимость, выбрав его так, чтобы при всех x внутри интервала локализации данного корня модуль производной функции (x) был меньше единицы, т.е.
|
|
|
|
|
|
|
|
|
1 |
(1.6) |
|
|
|
|
|
||||||
|
|
(x) |
|
|
1 f (x) |
|
||||
Таким образом, −1 < 1 + ′ |
< 1 |
или −2 < ′ |
< 0 для |
|||||||
случая, когда ′ |
> 0 и 0 < ′ |
< 2 в случае ′ < 0. |
|
|||||||
Метод простых итераций имеет линейную скорость сходимости, правильный выбор начального приближения позволяет уменьшить количество итераций для достижения заданной точности вычисления корня.
В практических инженерных расчетах часто, в качестве критерия окончания итерационного процесса, применяют сравнение аргумен-
тов на текущей и предыдущей итерациях: |
|
( ) − ( −1) ≤ |
(1.7) |
18

1.3 Метод Ньютона (метод касательных)
Метод Ньютона является одним из наиболее эффективных численных методов решения самых разных нелинейных уравнений. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643—1727). Поиск решения осуществляется путѐм построения последовательных приближений и осно-
ван на принципах метода простых итераций. Метод Ньютона называют также методом касательных, т.к. новое приближение x(k+1) явля-
ется абсциссой точки пересечения касательной, проведенной в точке (x(k) , f(x(k)) к графику функции f(x), с осью Ox (см. рисунок 1.9).
Постановка задачи. Пусть уравнение f(x) имеет один корень на отрезке [a,b], причем первая и вторая производные ′ ( ) и ′′ ( ) на этом отрезке существуют, непрерывны и сохраняют на отрезке постоянные знаки. Требуется определить этот корень с заданной точностью .
y |
|
|
|
f (x0) |
|
|
|
y=f(x) |
|
|
|
|
|
f '(x0) |
|
a |
|
|
b=x0 |
0 |
|
x2 |
x1 |
x |
Рисунок 1.9 – Метод Ньютона (касательных)
Внутри отрезка локализации корня [a,b] назначаем (смотри рисунок 1.9) начальное приближение корня x0 . В точке x0 , f (x0 ) рассчитываем касательную к кривой y f (x). Уравнение этой касательной имеет вид:
y f (x0 ) f (x0 ) x x0
19
Абсциссу точки пересечения касательной с осью Ox принимаем за следующее приближение корня, т.е.
x1 |
x0 |
|
f (x0 ) |
|
f (x0 ) |
||||
|
|
|
Повторяем процесс: проводим касательную к кривой y f (x) в точке x1 , f (x1 ) , абсциссу точки пересечения касательной с осью Ox принимаем за следующее приближение корня:
x2 |
x1 |
|
f (x1) |
|
f (x1) |
||||
|
|
|
В общем виде формула метода касательных имеет вид:
xn 1 |
xn |
f (xn ) |
(1.8) |
|
f (xn ) |
||||
|
|
|
Процесс повторяется до тех пор, пока не будет выполнено условие нахождения корня с заданной точностью. В инженерной практике, берут один из следующих критериев останова:
1. f(x(n))< - значение функции на данной итерации стало меньше заданного .
2. ( ) − ( −1) ≤ изменение x(n) в текущей итерации стало меньше заданного .
Чаще всего используют критерий 2. Условие сходимости метода Ньютона:
1.функция f(x) на отрезке локализации корня [a,b] непрерывна;
2.первая и вторая производные ( f´(x) и f"(x) ) непрерывны на интервале [a,b] и могут быть вычислены в любой точке интервала, причем первая производная не обращается в ноль;
3.вторая производная на интервале [a,b] постоянна по знаку;
4.начальное приближение х0 выбирается так, чтобы выполнялось условие
( 0) ∙ "( 0) > 0
20
