Теория матана

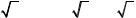
f 0 lim f x lim

sinx

2

2 1 2 .

x

x 0

x 0

3)

этот предел равен f x0 – значению функции f x в точке

x0 , т.е.:

lim f x f x0 .

(23)

x x0

Так как x0

lim x , то равенству (23) можно придать следующую форму:

x x0

lim f x f

lim x

.

x x0

x x0

Следовательно, для непрерывной функции символы lim и f

можно переставить.

Разность

x x0

называют приращением аргумента и обозначают

x, а разность

f x f x0 называют прира-

щением функции,

соответствующим данному приращению аргумента x, и обозначают

y , т.е.

lim

y 0 .

(24)

x 0

Операции над непрерывными функциями

1)

Пусть

функции

f x

и

g x

непрерывны

в

точке

x0 .

Тогда

функции

f x g x , f x g x ,

f x

g

x 0

также непрерывны в точке x0 .

g x

2) Переход к пределу под знаком непрерывной функции.

Если функция u x

в точке x0

имеет предел

A, а функция

f u

непрерывна в точке u A,

то сложная функция f x в точке x0 имеет предел, равный

f A , иными словами:

lim f

x

f

lim

x

.

(25)

x x

x x

0

0

3) Непрерывность сложной функции.

Если

функция u x

непрерывна

в

точке

x0 , а

функция y f u

непрерывна

в точке

u0

x0 , то сложная функция y f x непрерывна в точке x0 , т.е.

lim f x f x0 .

(26)

x x0

4)

Основные

элементарные

функции

ax , x , loga x, sinx, cosx,

tgx,

ctgx,

arcsin x, arccosx, arctgx, arcctgx непрерывны во все точках, где они определены. Любая функция

элементарные функции, за исключением нулей знаменателей.

Точки разрыва функции

Пусть функция

f x определена в некоторой окрестности точки x0 . Точку x0 называют точкой

разрыва функции

f x

в следующих случаях:

1) функция

f x

не определена в точке x0 ;

2) функция

f x

определена в точке x0 , но:

а) не существует lim f x ;

x x0

б) существует lim f x , но lim f x f x0 .

x x0

x x0

Если существует lim f x , но

f x не определена в точке

x0

или lim f x f x0 , то x0 на-

x x0

x x0

сторонние пределы

lim f x f x0 0 ,

lim

f x f x0 0 , то x0

называют точкой разрыва типа

x x0 0

x x0 0

“скачок”, а разность

f x0 f x0 0 f x0

0 – скачком функции

f x в точке x0 . Устранимый

на промежутке a;x0

x0;b , называют непрерывной слева в точке x0 (непрерывной справа в точке

0

x x0 0

f

x

f

0

x x0 0

f

x

f

0

.

x ), если

lim

x

lim

x

2

11

x

x, если x 1

16

x2

1

1) f x

1

;

2)

f x

.

, если x 1

x

2 3x 2

1

3 5

x

Решение. 1) Функция не определена в точке x 0

и поэтому в ней разрывна. Кроме того, точкой воз-

lim f x 0,

1

1

1

1

1

так

как

, 5

x

,

0

при

x 0 ;

lim

,

так

как

1

1

x 0

x

3 5x

x 0

3 5x

3

1

1

1

1

x 0 . Следовательно, lim f x lim f x , в точке

, 5

x

0,

при

x 0

функция

1

x

3 5x

3

x 0

x 0

0 f

0 0

1

1

имеет

разрыв

1-го

рода

–

скачок:

скачок

в

точке

x 0

равен f

.

3

3

2

11

5

1

5

5

lim

f x lim

x

x

, lim

f x

lim

, f 1

.

1

x 1 0

x 1 0

16

16

x 1 0

x 1 0

16

16

3 5x

Следовательно,

lim

f x

lim

f x lim f x f 1 ,

в точке

x 1функция непрерывна.

Эскиз

x 1 0

x 1 0

x 1

графика около точки разрыва дан на рис. 1.

2) Функция определена и непрерывна во всех точках, кроме x 1,

x 2, в которых знаменатель обраща-

ется в ноль. Исследуем эти точки. Для x 1:

x2 1

0

x 1 x 1

x 1

lim

lim

lim

2

2

3x 2

x 1 0 x

0

x 1 0 x 1 x 2

x 1 0 x 2

lim

x2 1

lim

x 1

2 .

x 1 0 x2 3x 2

x 1 0 x 2

Следовательно,

lim

f x lim

f x lim f x 2 ,

но f x не существует в точке

x 1. В точке

x 1 0

x 1 0

x 1

x 1

– устранимый разрыв. Чтобы доопределить функцию до непрерывности в этой точке,

полагаем

f 1 lim f x 2.Для

x 2:

lim

x2 1

lim

x 1

т.к. x 1 3,

x 2 0 и

x 2 0;

x 1

x 2 0 x2 3x 2

x 2 0 x 2

x2 1

x 1

lim

lim

,

т.к. x 1 3,

x 2 0 и

x 2 0. Следовательно,

в точке

x 2 раз-

x 2 0 x2 3x 2

x 2 0 x 2

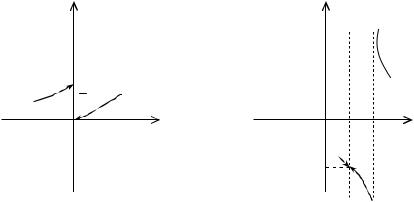
рыв 2-го рода. Эскиз графика около точек разрыва дан на рис. 2.

y

y

0

x

0 1 2

x

-2

СОДЕРЖАНИЕ.

1.

Числовая последовательность и ее предел

2

2.

Предел последовательности

2

3.

Правила предельного перехода

4

последовательности

4

5.

2-й замечательный предел

5

последовательностей

6

7.

Предел функции в точке

10

8.

Теоремы о пределах

12

9.

Предел функции в бесконечности

13

10.

Бесконечно малые и бесконечно большие функции

13

11.

Техника нахождения пределов

14

Применение к нахождению пределов

17

13.

Непрерывность функции

20