Федеральное государственное образовательное учреждение

высшего профессионального образования

НОВОУРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ

Кафедра высшей математики

Учебно – справочное пособие по курсу «ВЫСШАЯ МАТЕМАТИКА»

для студентов всех специальностей заочной формы обучения

Новоуральск 2007

УДК 519 О − 66

ББК 22.171

МиМ − 2.3. − __________ −07

Интегрирование.

Учебно – справочное пособие по курсу «ВЫСШАЯ МАТЕМАТИКА» для студентов всех специальностей заочной формы обучения

Новоуральск, изд. НГТИ. − 32 с.

Автор: старший преподаватель кафедры высшей математики НГТИ

Орлов Юрий Владимирович.

Пособие содержит 10 задач контрольной работы по теме «Интегралы и их применение» и справочник по данной теме.

Пособие обсуждено на заседании кафедры высшей математики НГТИ и рекомендовано к использованию в учебном процессе студентами всех специальностей заочной формы обучения.

“ ____ ” ______________ 200 ___ г.

Зав. кафедрой к.ф.м.н. ___________________ А.П. Золотарёв

Согласовано:

Председатель методической комиссии:

Профессор, д.т.н _____________ А.Е. Беляев

Содержание

	Введение ………………………………………..	4
	1 Контрольное задание:
	Задача №1 …………………………………......	5
	Задача №2 ….……………………………….....	7
	Задача №3 …………………………………......	9
	Задача №4 …………………………………......	10
	Задача №5 …………………………………......	11
	Задача №6 ….……………………………….....	13
	Задача №7 …………………………………......	15
	Задача №8 …………………………………......	16
	Задача №9 …………………………………......	19
	Задача №10 .……………………………….....	20
	2 Справочник………..………………..................	21
	Рекомендуемая литература …..……………	31

Введение

Данное пособие является сборником заданий второй контрольной работы (по теме «Интегралы и их применение») во втором семестре изучения курса «Высшая математика». Задания составлены для студентов заочной формы обучения, но могут выдаваться студентам и дневной и вечерней форм обучения. Первая контрольная работа в данном семестре выполняется по теме «Пределы, непрерывность и дифференцирование функции одной переменной».

Каждый студент при решении данной контрольной работы должен выполнить десять задач, которые заключаются в нахождении неопределенных, вычислении определенных интегралов либо в их применении. В соответствии с порядковым номером студента в списке группы в очередном задании выполняется соответствующий номер и решение всех задач оформляется в соответствии со стандартом НГТИ оформления текстовой документации.

Для удобства освоения данной темы пособие содержит справочник с таблицей интегралов и основными методами интегрирования. Более подробное изложение таких методов интегрирования можно изучить в литературе, список которой приведён в конце пособия.

1 Контрольное задание

Задача №1 Найти неопределенный интеграл, выполнив необходимые замены

Задача №2 Вычислить определенный интеграл, выполнив необходимые замены

Задача №3 Найти неопределенный интеграл, выполнив интегрирование по частям

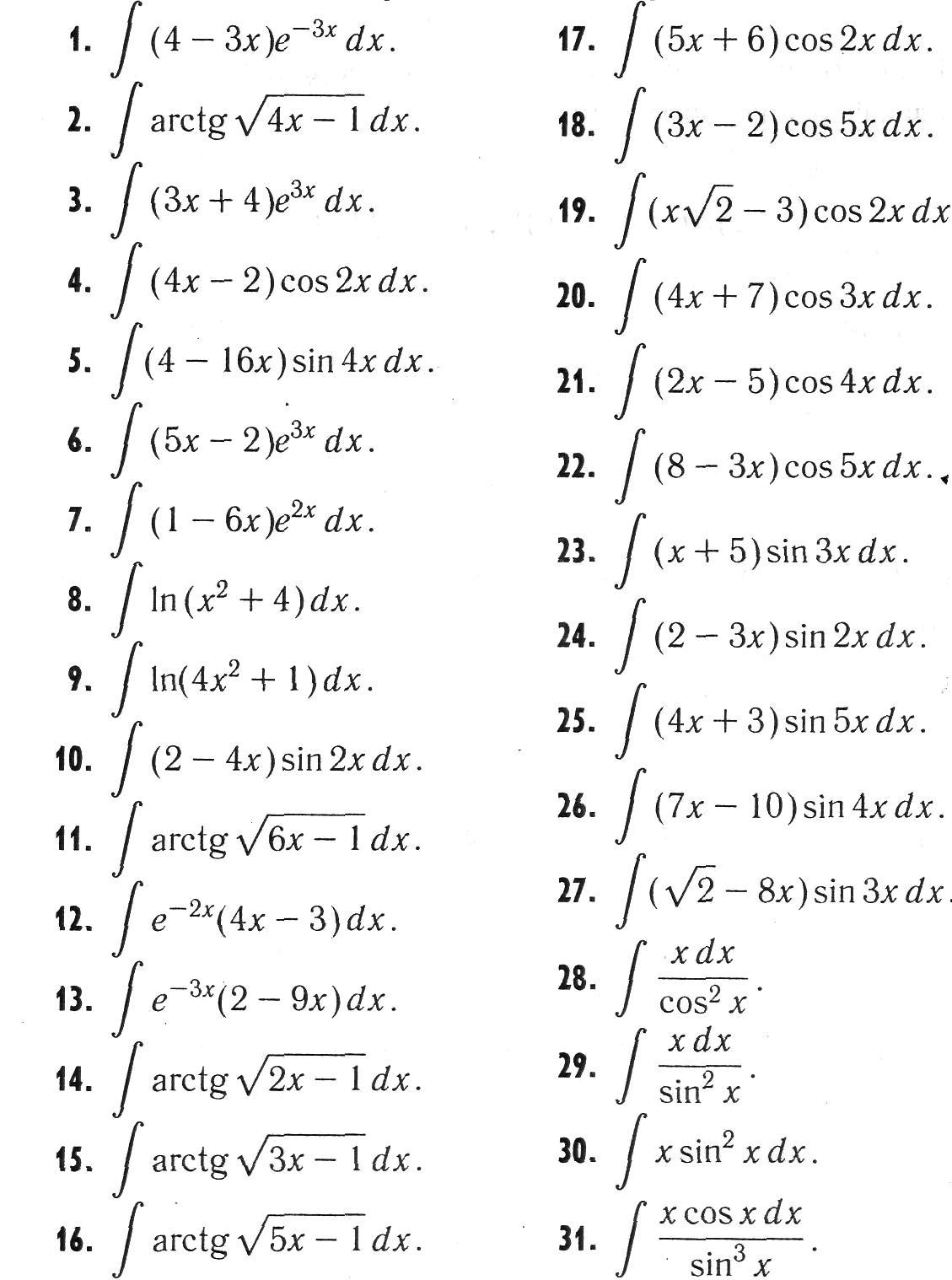
Задача №4 Вычислить определенный интеграл, выполнив интегрирование по частям

Задача №5 Найти неопределенный интеграл, разложив функцию на сумму элементарных дробей

Задача №6 Найти определенный интеграл от тригонометрических функций

Задача №7 Вычислить площадь фигуры, ограниченной линиями в декартовой системе координат

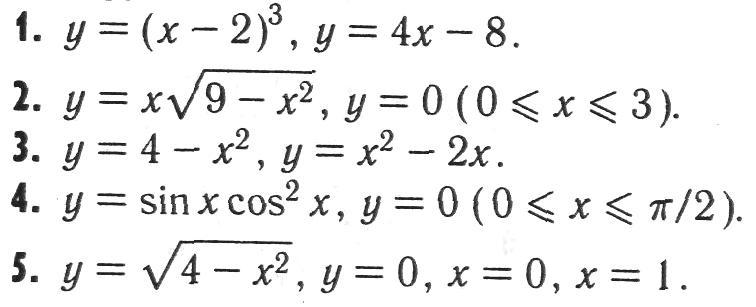
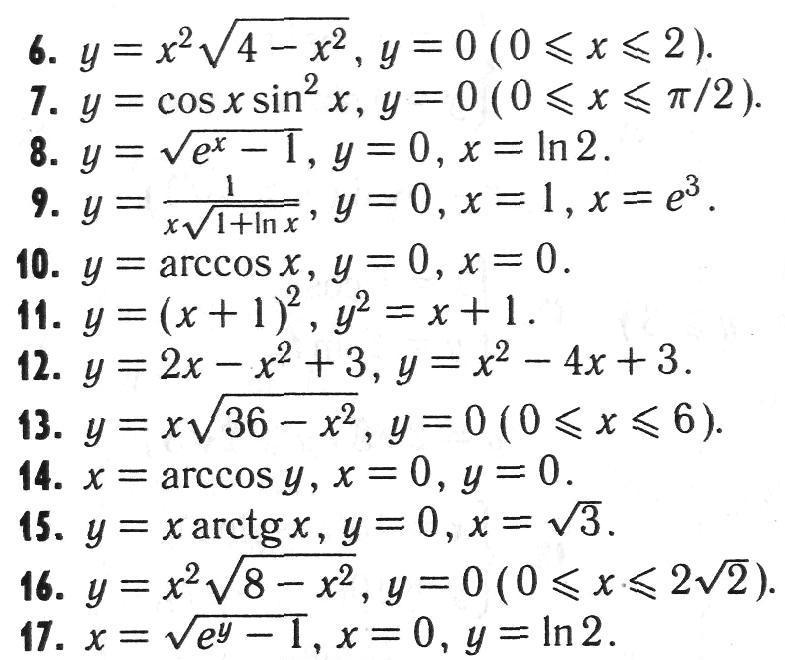
Задача №8 Вычислить площадь фигуры, ограниченной линиями в декартовой системе координат

Задача №9 Вычислить площадь фигуры, ограниченной линиями в полярной системе координат

Задача №10 Вычислить объём тела, образованного вращением фигуры, ограниченной графиком функции. В вариантах 1 – 16 ось вращения ОХ, а в вариантах 17 – 32 ось вращения ОY.

Справочник

• Функция F(x) является первообразной для f(x) если ;

• Если то ;

• Таблица основных интегралов

Функция	Первообразная	Функция	Первообразная
		1	х

• Определённый интеграл ;

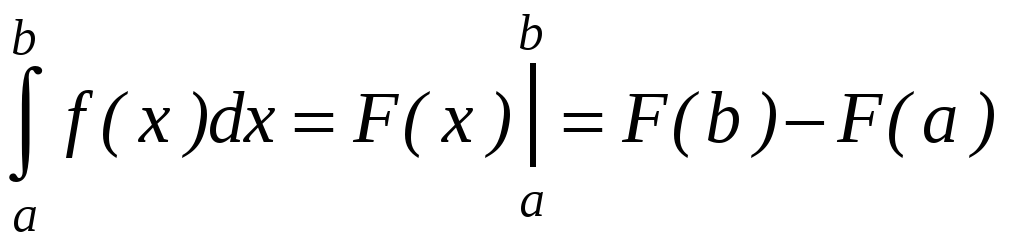• Замена переменной а);

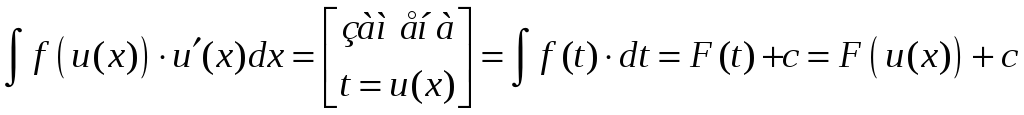б) ;

• Интегрирование по частям

• Разложение на элементарные дроби

а) неправильная дробь,

выделение целой части и правильной дроби:

,

;

б) ,

,

,

,

;

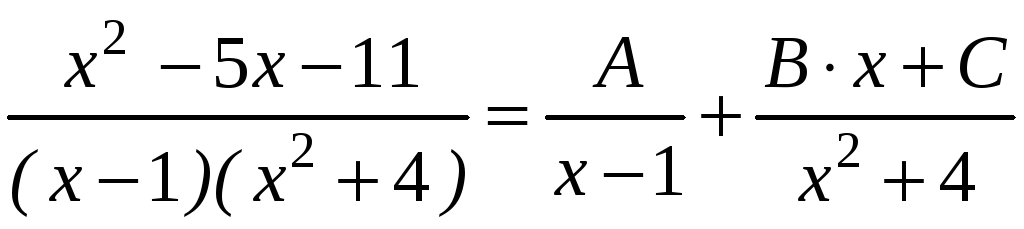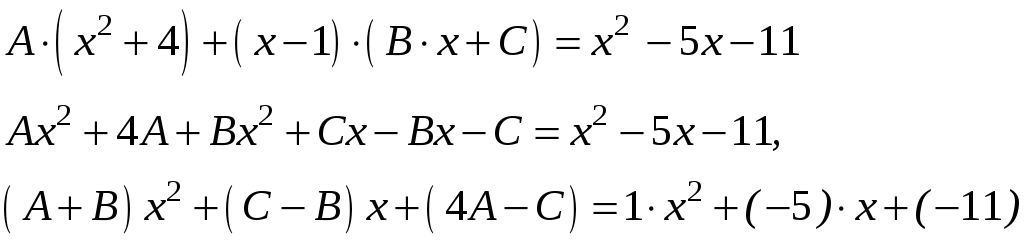
• Примеры разложений правильной дроби (дробно-рациональной функции) на сумму элементарных дробей

,

,

,

число коэффициентов каждый раз равно порядку многочлена в исходном знаменателе;

• Интегралы от элементарных дробей:

1) ;

2) ;

3) ;

5) Интеграл вида при находится по формуле

;

• Интегрирование тригонометрических функций

Пусть -рациональное выражение от .

Тогда

а) находится с помощью универсальной подстановки

,

получим интеграл от дробно-рациональной функции;

б) или при чётности подынтегральной функции относительно синуса и косинуса находится с помощью подстановки

;

в)

в.1) – любое замена ;

в.2) – любое замена ;

в.3) -нечётное положительное, – любое замена

-нечётное положительное, – любое замена

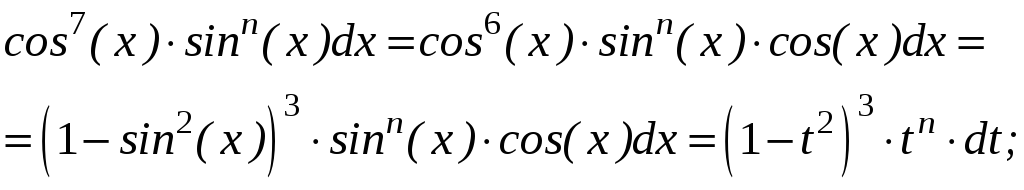
в.5) – чётные положительные числа, тогда каждую степень

понижают вдвое по формулам

г) При интегрировании произведения тригонометрических функций используются формулы

,

,

;

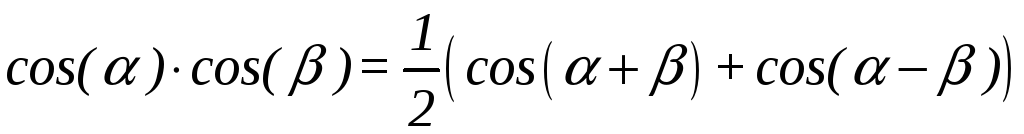• Площадь фигуры в декартовых координатах:

а) Площадь криволинейной трапеции, ограниченной осью ОХ, прямыми слева, справа, и графиком функции при условии ;

Если , то ;

б) Площадь между графиком и осью ОY

в) Если фигура ограничена в декартовых координатах графиком функции снизу, графиком сверху, вертикальными прямыми слева и справа, то;

• Площадь между параметрически заданной линией

при и осями декартовой системы координат:

г.1) С осью ОХ ;

г.2) С осью ОY ;

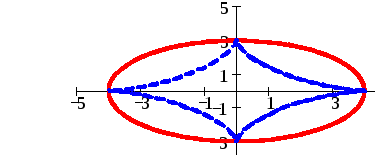
• Линия является эллипсом с полуосями 4 и 3.

• ;

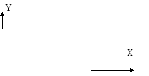
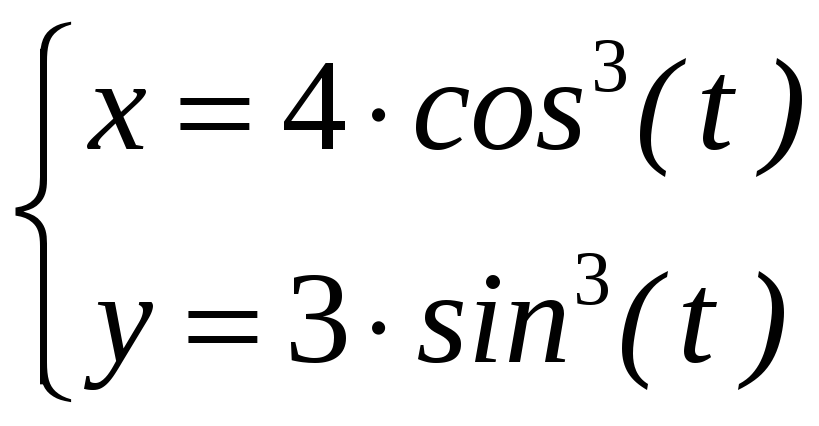
• Циклоида (заданная параметрически)

При а=1

• Линии в полярных координатах

-угол поворота от полярной оси (оси ОХ) против часовой стрелки, -расстояние до полюса (начала координат).

r

M

Полярная ось

Полюс

• Примеры линий в полярных координатах

• Площадь в полярных координатах:

Если фигура ограничена исходящими из полюса лучами ,

и линией , то площадь такого криволинейного сектора ;

Если фигура ограничена исходящими из полюса лучами ,

и линиями ближе к полюсу, дальше от полюса, то площадь такой фигуры ;

• Объём тела

а) Если для любой проекции тела на ось ОХ известна площадь поперечного сечения такого тела,

то его объём тела ;

б) Если в плоскости ХОY задана линия и при она вращается вокруг оси ОХ, то объём тела вращения

;

Если в плоскости ХОY задана линия и при она вращается вокруг оси ОY, то объём тела вращения

.

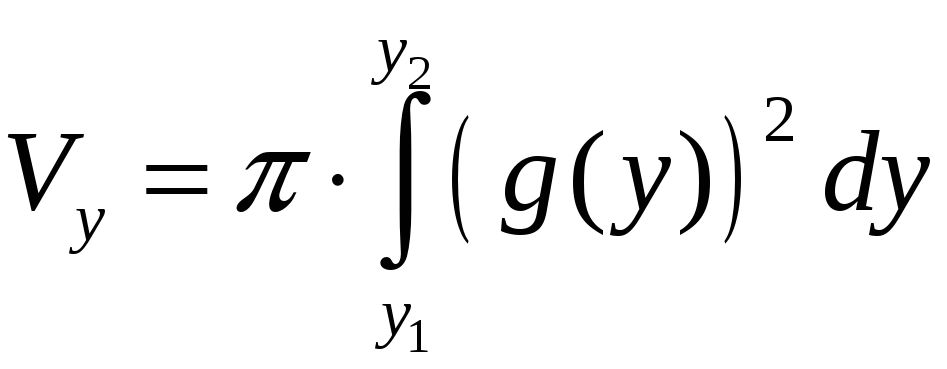Рекомендуемая литература

1) Шнейдер В.Е., Слуцкий А.И., Шумов А.С.

Краткий курс высшей математики (в двух томах).

Т.1. – М.: Высшая школа, 1978.-530 с.;

2) Пискунов Н.С. Дифференциальное и интегральное исчисление

для ВТУЗов. Т.1. – М.: Наука, 1978 – 560с.;

3) Бугров Н.С., Никольский С.М.

Высшая математика. Дифференциальное и интегральное

исчисление. – М.: Наука, 1981.-432 с.;

4) Данко П.Е., Попов А.Г., Кожевникова Т.Я.

Высшая математика в примерах и задачах (в двух частях).

Ч.1. – М.: Высшая школа, 1986 – 304, 416 с.;

5) Задачи и упражнения по математическому анализу для ВТУЗов.

под ред. Демидовича Б.П. – М.: Наука, 1972.- 632 с.;

6. Шипачев В.С. Высшая математика: Учебное пособие для ВУЗов.

– М.: Высшая школа, 1996 – 320 c.;

7) Власов В.Г. Конспект лекций по высшей математике.

– М.: Айрис, 1998 – 288с.

УДК 519 О − 66

ББК 22.171

МиМ − 2.3. − __________ −07

Орлов Юрий Владимирович

Интегрирование.

Учебно – справочное пособие по курсу «ВЫСШАЯ МАТЕМАТИКА» для студентов всех специальностей заочной формы обучения

Новоуральск, изд. НГТИ, 2007 − 32 с.