Занятие 10 Прямые в пространстве
Основные типы уравнений прямой линии
Векторно-параметрическое уравнение прямой линии:
.
(12)
Каноническое уравнение прямой:
(13)
Отметим, что одновременно l, m, n не могут обратиться в 0.
Уравнения (13) можно рассматривать как сокращенную форму записи, например, такой системы:
Связкой прямых будем называть совокупность прямых пространства, проходящих через фиксированную точку, либо попарно параллельных.
Прямую L назовем общим перпендикуляром к прямым L1 и L2, если она перпендикулярна к каждой прямой и с обеими пересекается.
Основные утверждения
Пусть 
–
радиус-вектор фиксированной точки
прямой l, a
–
направляющий вектор прямой L.
Тогда уравнение
,
где t - параметр, принимающий действительные значения, будет уравнением прямой L.
Пусть прямая L
в пространстве проходит через точку 
параллельно вектору 
.
Тогда ее координатно-параметрические
и канонические уравнения, соответственно,
имеют вид
x=x0+lt, y=y0+mt, z=z0+nt,
Если 
–
направляющий вектор прямой L
в пространстве и 
–
радиус-вектор фиксированной точки
прямой L,
то уравнение
является уравнением прямой L.
Если прямая L в пространстве является пересечением двух плоскостей, заданных общими уравнениями, т.е. ее точки удовлетворяют системе уравнений
то в качестве направляющего вектора прямой можно выбрать следующий вектор:
Утверждение 5.
Если прямая L
на плоскости задана нормальным уравнением
и 
–
произвольная точка плоскости, то
расстояние 
от точки М
до прямой L
определяется формулой
.
Пусть в пространстве
точка М
имеет координаты 
,
прямая L
проходит
через точку 
параллельно
вектору 
,
система координат прямоугольная.
Тогда расстояние 
от точки М
до прямой L
будет следующим:
.
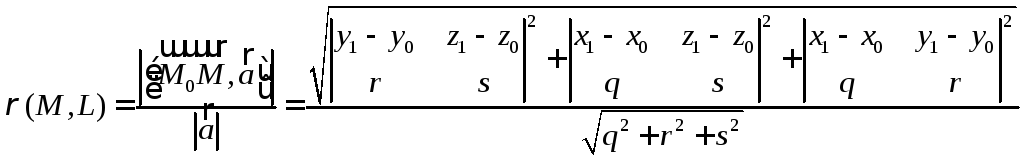Пусть в пространстве
заданы две непараллельные прямые L1
и L2,,
имеющие направляющие векторы 
и 
,
проходящие через точки 
и 
соответственно. Система координат
прямоугольная. Тогда уравнение общего
перпендикуляра задается системой
уравнений:
,
,
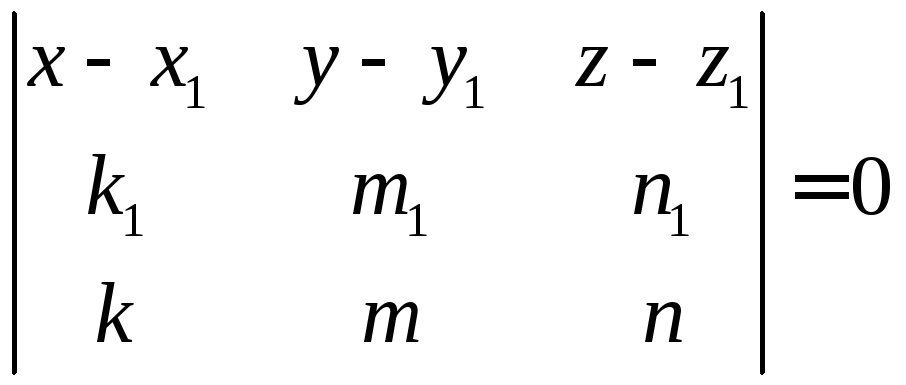где
.
Если L1
и L2
– скрещивающиеся
прямые, которые проходят через точки
M1(x1,
y1,
z1)
и M2(x2,
y2,
z2)
параллельно векторам 
и 
соответственно, то расстояние 
между прямыми L1
и L2
можно определить по формуле 
,
где 
,
.
Если П – алгебраическая поверхность (линия L) порядка k и l – прямая, то число точек пересечения поверхности П (линии L) и прямой l не превосходит k.
Задача 82. Найти
необходимые и достаточные условия, при
которых прямые 
и 
1) пересекаются (т.е. имеют единственную общую точку);
2) скрещиваются;
3) параллельны, но не совпадают;
4) совпадают.
Задача 83. Даны две прямые. Установить, пересекаются они, скрещиваются, параллельны или совпадают. Если прямые пересекаются или параллельны, составить уравнение плоскости, в которой они лежат. Если прямые пересекаются, найти также координаты точки их пересечения.
1) 
и 
2) 
и 
3) 
и 
4) 
и 
5) 
и 
Задача 84. [2,6.28]
Составить уравнение плоскости, проходящей
через точку 
и параллельной прямым 
и 
.
Задача 85 (с решением). Написать каноническое уравнение прямой, проходящей через точку (1,1,1) и параллельной плоскостям x+3y–4z+1 = 0, x= 0, а так же записать векторно-параметрическое и параметрическое уравнение этой прямой.
Решение. Для того чтобы написать каноническое уравнение данной прямой, надо знать точку, через которую она проходит, и направляющий вектор. Направляющий вектор находим по формуле
.
Каноническим уравнением данной прямой будет уравнение
,
векторно-параметрическим
,
где 
=(1,1,1),
= (0, –4, –3), параметрическим x
= 1, y
= 1–4t ,
z
= 1-3t.
Задача 86(с решением).
Составить уравнение перпендикуляра,
опущенного из точки (3, 2, 1) на прямую 
.
Решение.
Искомый перпендикуляр 
лежит в плоскости π,
ортогональной заданной прямой l,
направляющий вектор которой равен 
.
Поэтому уравнение плоскости π
имеет вид
2x+4y+z+D=0,
где константу D
определяем из условия, что 
π:
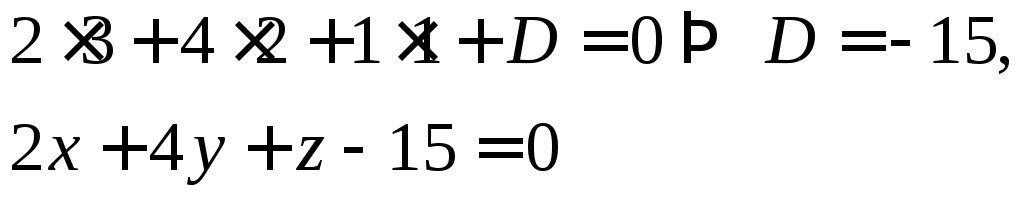
есть искомое
уравнение плоскости. Основание
перпендикуляра 
имеет координаты (
),
удовлетворяющие соотношениям
,
2x
+4y
+z
-15=0,
откуда получаем
(
).
Следовательно, искомая прямая описывается соотношениями
или
.
Задача 87 (с решением). Найти проекцию прямой
2x+3y+4z+5=0,
x-6y+3z-7=0
на плоскость 2x+2y+z–15=0.
Решение.
Искомая проекция может быть задана как
прямая пересечения плоскости π
2x+2y+z+5=0
с ортогональной к ней плоскостью π,
проходящей через заданную прямую l.
Последнее означает, что плоскость π
является элементом пучка, образованного
плоскостями π
2x+3y+4z+5=0
и π2
x-6y+3z-7=0.
Следовательно,
уравнение π
имеет вид 
Условие ортогональности
плоскостей π и π
дает
откуда
и уравнение плоскости π есть 4x-9y+10z-9=0, а уравнение ортогональ-ной проекции
2x+2y+z-15=0,
4x–9y+10z–9=0.
Задача 88. Составить
уравнение плоскости, проходящей через
точку 
и прямую, заданную уравнениями:
1) 
2) 
Задача 89. Составить
уравнение прямой, проходящей через
точку 
и пересекающей две данные прямые:
1)
и 
2) 
и 
Задача 90. Найти угол между прямыми:
1) 
и 
2)
и 
Задача 91. Плоскости
являются соответственно плоскостями
новой системы координат, а точка 
имеет в новой системе координаты (1,1,1).
1) Найти координаты
точки в исходной системе координат,
если известны ее координаты 
в новой системе координат.
2) Составить в новой
координатной системе канонические
уравнения прямой, которая в исходной
системе задается уравнениями 
.