Занятие 12 Классификация кривых второго порядка на плоскости
Основные утверждения
Пусть в декартовой системе координат задано уравнение
Ах2 + 2Вху + Су2 + 2Dx + Ey + f =0.
Тогда существует такая прямоугольная система координат, в которой
это уравнение принимает один из следующих девяти канонических видов:
1. 
– эллипс.
2. 
– мнимый эллипс (пустое множество).
3. a2 x2+b2y2 = 0 – пара мнимых пересекающихся прямых 1 точка.
4. 
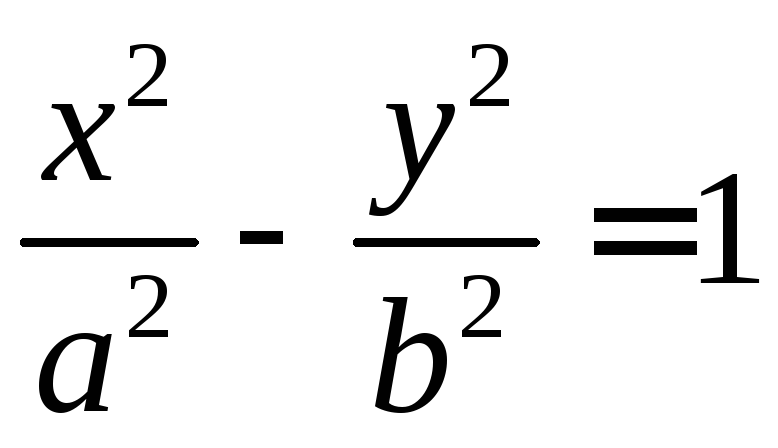– гипербола.
5. a2 x2-b2y2 = 1 – пара пересекающихся прямых.
6. у2 ='2рх – парабола.
7. у2 – а2 = 0 – пара параллельных прямых.
8. y2 + а2 = 0 – пара мнимых пересекающихся прямых (пустое множество).
9. у 2 = 0 – пара совпавших прямых.
Задача 101 (с решением). Пусть в некоторой прямоугольной системе координат кривая второго порядка задана уравнением
.
Найти ее канонический вид и каноническую систему координат.
Решение.
Здесь A=5,
B=2,
C=8.
В данном случае 
и
поэтому надо осуществлять поворот
исходной системы координат на угол,
который определяется условием
или 
Известна связь
между 
и 
:
откуда получаем уравнение
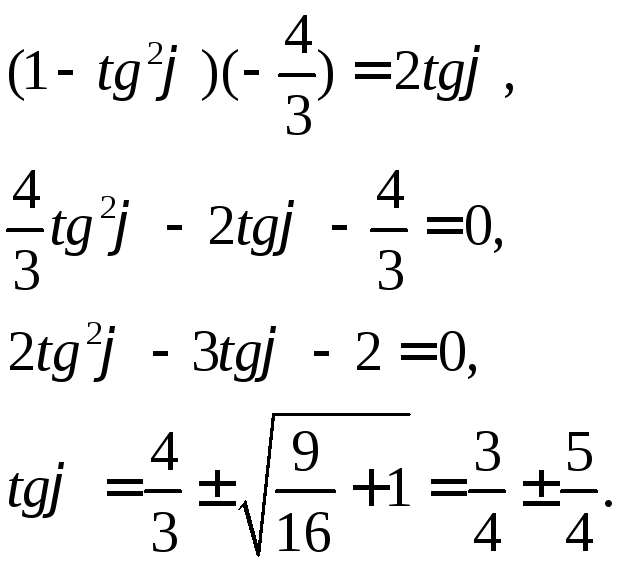
Для 
имеем 2 значения 
Выберем
одно из них, например, 
Для того, чтобы применять формулы связи координат одной и той же точки при повороте одной прямоугольной системе координат относительно другой:
надо знать такие
функции угла поворота φ,
как 
и
.
Вспоминаем формулы связи между 
Можно брать либо обе формулы со знаком +, либо со знаком -.
Имеем в данном случае при выборе знака +:
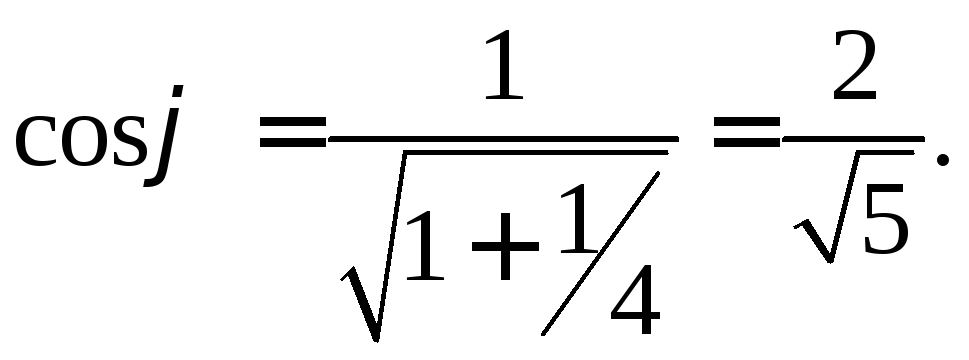
Итак, связь координат осуществляется по формуле
В этой новой системе координат имеем уравнение
Раскрываем скобки:
Выделяем
полные квадраты:
Если ввести новые
переменные 
то в этих переменных наше уравнение
имеет канонический вид
Для того, чтобы построить график данной кривой, вычисляем связь между координатами в исходной системе координат и самой последней из рассмотренных:
Эти формулы говорят
о том, что начало новой системы координат
имеет во второй системе координат
координаты (2,3), базисные векторы имеют
во втором базисе координаты 
.
Для более точного изображения эллипса в старой системе координат найдем его точки пересечения с осями координат: при x=0
имеем 2 точки пересечения; если положить y=0, то точки пересечения определяются из уравнения
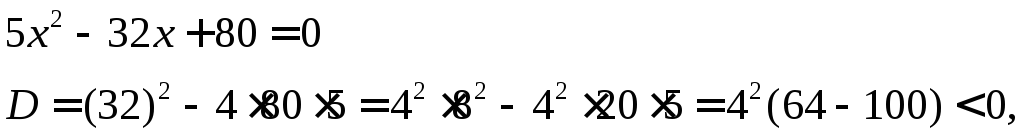
точек пересечения с осью абсцисс нет.
Задача 102. Определить тип кривой 2-го порядка, составить ее каноническое уравнение и найти каноническую систему координат:
1) 
2) 
Занятие 13 Канонические уравнения поверхностей второго порядка
Основные определения
Эллипсоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение
Однополостным гиперболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение
Двуполостным гиперболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение
Эллиптическим параболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение
Гиперболическим параболоидом называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение
Эллиптическим цилиндром называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение
Гиперболическим цилиндром называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение
Параболическим цилиндром называется поверхность, которая в некоторой декартовой прямоугольной системе координат имеет уравнение
у2 = 2рх.
Основные утверждения
Утверждение 1. Общее уравнение поверхности второго порядка в общей декартовой системе координат
имеет в канонической прямоугольной системе координат один из 17 канонических видов. из которых 8 – перечисленные поверхности, остальные представляют собой плоскости (2 или 1), линии, точки или пустое множество.
Задача 103. (с решением). Вывести уравнение сферы с центром в точке C(xo, yo, zo радиуса r.
Решение. Сфера есть множество точек, находящихся на расстоянии r от точки C(xo, yo, zo). Введем в пространстве декартову прямоугольную систему координат. Точка M(x, y, z) лежит на сфере S тогда и только тогда, когда длина отрезка CM равна r или тогда и только тогда, когда CM2=r2 . Расстояние между точками M и C равно
Поэтому уравнение окружности будет иметь вид
В частности, уравнение сферы радиуса r с центром в начале координат имеет вид:
