Занятие 4 Проекции. Скалярное произведение векторов

Основные определения

Число, равное будем называть скалярным произведением векторов и , обозначая его (,).

Примечание. Скалярное произведение является числовой функцией двух векторных аргументов.

Система векторов называется ортогональной, если скалярное произведение любых двух векторов и , при равно нулю.

Ортогональная система векторов называется ортонормированной, если векторы этой системы имеют единичную длину.

Основные утверждения

Скалярное произведение как функция двух векторных аргументов обладает следующими свойствами:

1) - симметричность;

2) - линейность;

3) – положительная определенность.

Обратно, любая действительная функция двух векторных аргументов на плоскости или в пространстве, удовлетворяющая свойствам (1)-(3) совпадает со скалярным произведением.

Для любых двух векторов и справедливы утверждения:

1) (отметим, что нулевой вектор будем считать перпендикулярным ко всем векторам);

2)

3) , здесь - угол между векторами и ;

4) если - ортогональная проекция вектора на ненулевой вектор , то;

5) если - ортонормированный базис и координатные строчки векторов и в этом базисе и соответственно, то

Если – ортонормированный базис и – произвольный вектор, то

Задача 24. Дан равносторонний треугольник , длины сторон которого равны 1. Вычислить выражение

Задача 25. В треугольнике проведены медианы . Вычислить выражение

Задача 26. Найти скалярное произведение векторов и , если:

1) ;

2) ;

3) ;

4) и сонаправлены;

5) и противоположно направлены.

Задача 27. Найти скалярное произведение векторов и , заданных своими координатами:

1) ;

2) ;

3) .

Задача 28. Найти угол между векторами и , заданными своими координатами:

1) ;

2)

Задача 29. Найти расстояние между точками и , заданными своими координатами:

1)

2)

Задача 30. Дан вектор . Найти ортогональную проекцию вектора на прямую, направление которой определяется вектором , и ортогональную составляющую вектора относительно этой прямой, если вектор имеет координаты:

Задача 31. Объяснить геометрический смысл всех решений векторного уравнения , а также его частного решения, коллинеарного вектору :

1) в плоском случае;

2) в пространственном случае.

Задача 32. Дан произвольный тетраэдр . Доказать: если перпендикулярны ребра и и ребра и , то ребра и также перпендикулярны.

Задача 33. Найти сумму векторов, являющихся ортогональными проекциями вектора на стороны квадрата.

Задача 34. Найти из условия , где – некомпланарные векторы.

Занятие 5 Векторное и смешанное произведение векторов

Основные определения

Упорядоченная тройка некомпланарных векторов называется правой, если из конца третьего вектора кратчайший поворот от первого ко второму вектору виден совершающимся против часовой стрелки. В противном случае тройка называется левой.

Векторным произведением векторов и называется вектор , удовлетворяющий трем условиям:

1) вектор ортогонален векторам и ;

2) тройка ,, – правая;

3) .

Обозначим векторное произведение .

Смешанным произведением векторов ,, будем называть число, равное , обозначая его или (,,).

Прямоугольную таблицу чисел, состоящую из т строк и п столбцов будем называть матрицей размера , а матрицу размера будем называть квадратной порядка п.

Пусть задана квадратная матрица порядка 2

Определителем этой матрицы (определителем 2-го порядка) назовем число . Обозначать это число будем

Определитель третьего порядка определим следующим образом:

.

Основные утверждения

Смешанное произведение обладает следующими свойствами:

1) , если тройка – правая. , если тройка – левая (здесь – объем параллелепипеда, построенного на векторах ;

2) при перестановке любых двух сомножителей смешанное произведение принимает про­тивоположное значение;

3) если , то ;

4) векторы – компланарны.

Векторное произведение обладает следующими свойствами:

1)

2)

3)

4) ;

5), где – площадь параллелограмма, построенного на векторах и .

Если и , – координатные строчки соответственно векторов в базисе , то

1) ,

2) .

Если базис - ортонормированный, правый, то

3) ,

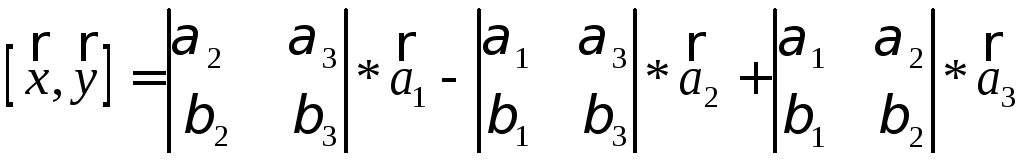4) .

Если ,, – вычисленные в некотором базисе координатные строчки векторов соответственно, то

компланарны

тройка имеет ту же ориентацию, что и тройка базисных векторов .

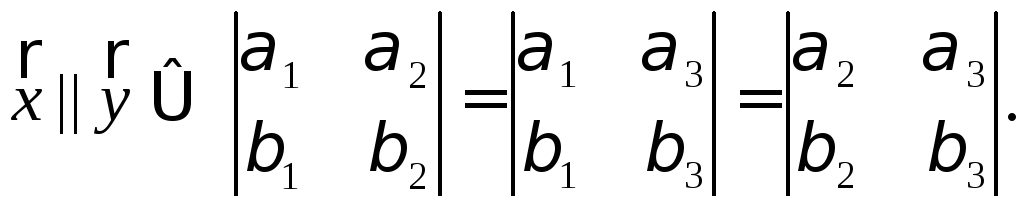
Определитель 3-го порядка обладает следующими свойствами:

1. _{При перестановке строк его значение меняется на противоположное;}

2)

3) ;

4) при транспонировании значение определителя не меняется: .

Задача 35.Упростить выражения:

1)

2) .

Задача 36. Векторы образуют:

1) ортонормированный правый базис;

2) ортонормированный левый базис;

3) ортогональный правый базис.

Выразить векторные произведения через векторы

Задача 37. Найти векторное произведение векторов и , заданных своими координатами:

1)

2)

3)

Задача 38. На векторах и отложенных из одной точки, построен треугольник. Найти площадь этого треугольника и длины трех его высот.

Задача 39. Доказать тождества:

1)

2)

3)

Задача 40. Найти смешанное произведение векторов и , заданных координатами:

1)

2)

3)

Задача 41. Проверить, компланарны ли векторы, заданные координатами в произвольном базисе:

1)

2)

Задача 42 (с решением). Параллелепипед ABCDA’B’C’D’ задан координатами вершин ребер, выходящих из вершины А с координатами А(1,2,3), В(9,6,4), C(3,0,4) и A’(5,2,6).

Найти длину ребра АВ, угол между ребром АВ и AC; площадь основания ABCD, объем параллелепипеда и вычислить высоту, опущенную из вершины А’. Система координат прямоугольная.

Решение.

C'D'

A' B'

C D

A B

Длина ребра AB – это длина вектора, т. е. длина вектора (8,4,1). . Один из углов между AB и AC будет определяться, как один из углов между векторами и по формуле

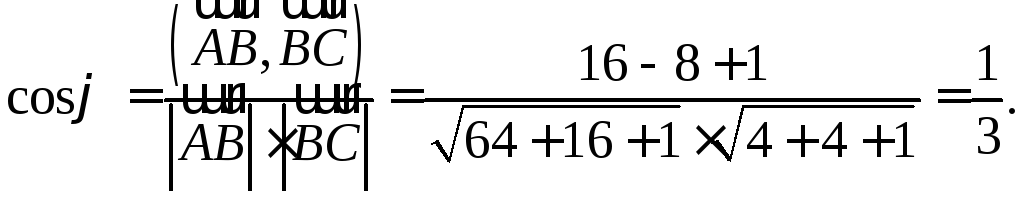
Площадь основания ABCD есть модуль векторного произведения векторов и :

И тогда

Объем параллелепипеда равен модулю смешанного произведения векторов, и (4,0,3). Поэтому

,

а .

С другой стороны, объем параллелепипеда есть произведение площади основания ABCD на высоту, опущенную из вершины A’, поэтому длину высоты можно получить, разделив объем параллелепипеда на площадь основания, т.е. она будет равна 48/26 = 24/13.

Задача 43. Даны точки являющиеся вершинами тетраэдра. Найти:

1) объем тетраэдра;

2) длину высоты тетраэдра, опущенной из вершины .

Задача 44. Доказать, что площадь выпуклого четырехугольника равна половине длины векторного произведения .

Задача 45. Найти необходимые и достаточные условия того, чтобы уравнение , где , имело решение. Найти общее решение этого уравнения.