Занятие 8 Уравнения прямых на плоскости

Основные типы уравнений прямой линии

Векторно-параметрическое уравнение прямой линии:

. (3)

Каноническое уравнение прямой линии:

. (4)

Договоримся, что, когда в уравнениях (4) какой-то знаменатель (l или m) равен 0, соответствующий числитель также равен 0. Одновременно все знаменатели обратиться в 0 не могут.

Примечание: Уравнение (4) является одной из форм записи общего уравнения прямой плоскости в пространстве.

Общее уравнение прямой линии:

Ах+Ву+С=0. (5)

Нормальное уравнение прямой линии:

xcos a+ysin a - p = 0. (6)

Заметим, что уравнение (6) есть частный вид уравнения (5) и уравнение (6) можно получить из (5), умножив уравнение (5) на число

Уравнение в отрезках:

является частным случаем уравнения (5).

Уравнение с угловым коэффициентом имеет вид: .

Пучком прямых линий будем называть совокупность прямых плоскости, проходящих через фиксированную точку, либо попарно параллельных.

Основные утверждения

Пусть – радиус-вектор фиксированной точки

прямой L, а – направляющий вектор прямой L. Тогда уравнение

где t – параметр, принимающий действительные значения, будет уравнением прямой L.

Пусть на плоскости задана прямая L, проходящая через точку M₀(x₀,y₀) параллельно вектору (l,п). Тогда ее координатно-параметрические уравнения имеют вид

x= x₀ + lt, y = y₀ + mt.

Общим уравнением прямой на плоскости в произвольной декартовой системе координат будет уравнение вида

Ax + By + С = 0,

где A² + B² 0.

Пусть – радиус-вектор фиксированной точки прямой L на плоскости и – ненулевой вектор, перпендикулярный к прямой L, тогда уравнение

=0

является уравнением прямой L.

Пусть на плоскости задана прямоугольная система координат и прямая L. Если р - расстояние от начала координат до прямой L, а a- угол между осью ОХ и лучом, перпендикулярным к L и пересекающимся с L, то общее уравнение можно представить в виде

x cos а + у sin а — р = 0.

Если прямая L на плоскости пересекает оси OX, OY в точках (а, 0), (0,b) и а, b 0, то общее уравнение этой прямой можно представить в виде

Пусть на плоскости задана прямоугольная система координат, прямая L составляет с осью ОХ угол и пересекает ось OY в точке (0, b). Тогда общее уравнение прямой можно представить в виде

у = kx + b.

Если на плоскости даны две точки: А(х₀, у₀) и В(х₁,y₁), то координатно-параметрические и канонические уравнения прямой (АВ) можно записать так:

x = х₀ + (x₁ – x₀) t, y = у₀ + (y₁ – y₀)t

и

Если прямая L на плоскости задана уравнением Ax+By+С = 0 и координаты вектора а есть (т,п), то

1) вектор будет параллельной прямой L в том и только в том случае, если выполняется условие Am + Вп = 0;

2) вектор (В,—А) будет направляющим вектором прямой L.

Прямые L₁ и L₂ на плоскости, задаваемые уравнениями A₁x+B₁y+С₁ = 0 и A₂x + B₂y + С₂ = 0, будут параллельны тогда и только тогда, когда существует  такое, что А₂ = A₁, В₂ = B₁ или

Прямые L₁ и L₂ совпадают, если А₂ = А₁, В₂ = B₁, C₂ = C₂.

Если A₁x + В₁y + C₁ = 0 и A₂x + В₂y + C₂ = 0 задают две различных прямых на плоскости, то любая прямая этого пучка задается уравнением

a_x + B₁y + C₁b_x + B₂y + C₂

где a и b - некоторые действительные числа, Три прямые на плоскости

L₁ : A₁x+B₁y+C₁=0, L₂ : A₂x+B₂y+C₂=0, L₃ : A₃x+B₃y+C₃=0

тогда и только тогда принадлежат одному пучку, когда выполняется условие

Если прямая L в плоскости задана в прямоугольных координатах уравнением Ax + By + С = 0, то вектор (A, В) перпендикулярен к прямой L.

Две точки M(x₁, y₁) и N(x₂, y₂) лежат в разных полуплоскостях относительно прямой Ax + By + С = 0 тогда и только тогда, когда числа Ах₁ + Ву₁ + С₁ и Ах₂ + Ву₂ + С₂ имеют противоположные знаки.

Пусть на плоскости в прямоугольной системе координат заданы урав­нения А₁x + В₁y + C₁ = 0 и А₂x + В₂y + C₂ = 0 прямых L₁ и L₂ соответственно. Тогда наименьший из углов между прямыми L₁ и L₂ можно вычислить по формуле

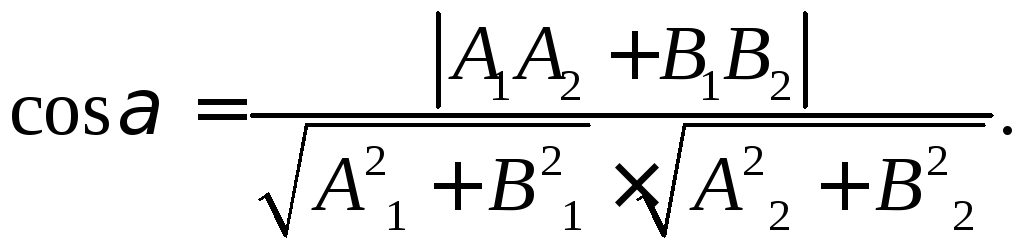
Задача 58. При каком необходимом и достаточном условии прямые и :

1) пересекаются в единственной точке;

2) параллельны, но не совпадают;

3) совпадают?

Задача 59. Записать уравнение прямой в виде

2) Записать уравнение прямой в параметрической и канонической формах.

3) Найти угловой коэффициент прямой .

Задача 60. Установить, пересекаются, параллельны или совпадают прямые данной пары; если прямые пересекаются, найти координаты точки пересечения:

1)

2)

3)

4) и

Задача 61. Даны две вершины треугольника (3, –1) и (1, 4) и точка пересечения его медиан (0,2). Найти координаты третьей вершины треугольника и составить уравнения его сторон.

Задача 62. Составить уравнения прямых, равноудаленных от трех точек и .

Задача 63.(с решением) Прямая линия на плоскости задана в общей декартовой системе координат уравнением x–3y–2=0. Задать ее в векторно-параметрическом виде, в параметрическом, через угловой коэффициент, как через 2 точки, в отрезках.

Решение. Для векторно-параметрического задания надо знать направляющий вектор и точку, через которую она проходит. За направляющий вектор прямой, заданной общим уравнением Ax+By+C=0, можно взять вектор (–B, A) . В данном случае A=1, B= -3 , поэтому за направляющий вектор берем (3, 1) , за координаты точки, через которую проходит прямая, – любую пару чисел, удовлетворяющую уравнению прямой. Например, положим x = 2 , тогда y = 0 , следовательно, точка (2, 0) лежит на прямой и векторно-параметрическое уравнение прямой есть где = (2,0), =(3, 1). В параметрической форме имеем x = 2 +3t, y = t. Заметим, что для того, чтобы вернуться к исходной записи, надо из этих уравнений исключить параметр t.

Если переписать общее уравнение прямой в виде y = x/3–2/3, то угловой коэффициент k равен 1/3. Для того чтобы написать уравнение прямой, проходящей через 2 точки, надо вычислить еще одну точку, лежащую на данной прямой. Возьмем x = 8 , тогда y = 2. Следовательно, уравнение нашей прямой можно записать также в виде или .

Переписав уравнение в виде , видим, что на осях координат отсекаются отрезки 2 и .

Задача 64 (с решением). Составить уравнение прямых, проходящих через точку (3,1) и образующих с прямой 3x–y–2 = 0 углы в 45^o . Система координат прямоугольная.

Решение.

y

l₁

135^o

l₂

A(3,1)

0 45^o x

l

Перепишем уравнение прямой l в виде y = 3x-2. Если прямая l образует с прямой l₂ угол _то с прямой l₁ угол _ и, следовательно, угловые коэффициенты для l₁ и l₂ могут быть найдены из соотношения

,

откуда получаем для k два значения k₁ = ½ , k₂ = –2. Осталось воспользоваться формулой прямой линии, проходящей через точку (3,1) с угловым коэффициентом ½ и –2: и .

Задача 65. Составить уравнение прямой, проходящей через точку и перпендикулярной прямой:

1)

2)

3)

4)

5)

Задача 66. На прямой найти точку, равноудаленную от точек и

Задача 67. Найти расстояние от точки до прямой, заданной своим уравнением:

1)

2)

3)

4)

5)

6)

Задача 68. Составить уравнения прямых, параллельных заданной прямой

и отстоящих от точки на расстояние .

64. Даны точка и прямая . Найти координаты:

1) проекции точки на прямую;

2) точки , симметричной с относительно прямой.

Задача 69. Даны уравнения сторон треугольника: Составить уравнение высоты, опущенной на третью сторону.

Задача 70. Точки и являются серединами оснований равнобедренной трапеции, а точки и лежат на ее боковых сторонах. Составить уравнения сторон трапеции.

Задача 71. Составить уравнение биссектрисы того угла между прямыми и , внутри которого лежит точка

Задача 72. На плоскости даны три точки и прямая . Составить уравнение этой прямой в новой системе координат .

Задача 73. Составить уравнения сторон квадрата, зная его центр (1,6) и по точке на двух непараллельных сторонах: , .