Занятие 6 Замена декартовой системы координат

Основные утверждения

Пусть в пространстве задана декартова система координат с началом в точке О и базисом ; вторая же система координат имеет начало в точке О' и базис . Положим, что координаты точки О' и векторов в первой системе координат будут соответственно , , Если при этом координаты точки М в первой системе координат есть , а во второй – , то справедливы формулы:

Задача 46. В пространстве даны два базиса и Векторы второго базиса имеют относительно первого базиса координаты , , соответственно.

1) Найти координаты вектора в первом базисе, если известны его координаты во втором базисе.

2) Найти координаты вектора во втором базисе, если известны его координаты в первом базисе.

3) Найти координаты векторов во втором базисе.

Задача 47. Координаты каждой точки пространства в системе координат О, выражаются через координаты этой же точки в системе формулами .

1) Выразить координаты через координаты

2) Найти координаты начала и базисных векторов первой системы координат во второй системе.

3) Найти координаты начала и базисных векторов второй системы в первой системе.

Задача 48. Найти координаты точки в системе координат , в пространстве, если известны ее координаты в системе координат , , ,

Задача 49. Дан правильный шестиугольник . Найти координаты точки плоскости в системе координат , если известны ее координаты в системе координат .

Задача 50. На плоскости даны две прямоугольные системы координат и , . Начало второй системы координат имеет в первой системе координаты (1,3), а векторы получаются из векторов , соответственно, поворотом на один и тот же угол в направлении кратчайшего поворота от к . Найти координаты точки в первой системе координат, если известны ее координаты во второй системе, считая угол равным:

Модуль II занятие 7 Общее понятие об уравнениях линий и поверхностей

Основные определения

Уравнение назовем общим уравнением линии L на плоскости (поверхности  в пространстве), если точка М(х,у) (M(x,y,z)) в том и только в том случае принадлежит линии L (поверхности ), когда ее координаты удовлетворяют заданному уравнению.

Параметрическими уравнениями линии L на плоскости будем называть систему уравнений

(1)

где и - действительные функции действительной переменной t такие, что точка М(х,у) принадлежит линии L тогда и только тогда, когда существует t, удовлетворяющее уравнениям (1). Для задания параметрических уравнений линии в пространстве к записанным двум уравнениям необходимо добавить уравнение для третьей координаты .

Параметрическими уравнениями поверхности  в пространстве будем называть систему уравнений

z= (2)

где и – действительные функции двух действительных переменных и и v такие, что точка M(x,y,z) принадлежит поверхности  тогда и только тогда, когда существуют u и v, удовлетворяющие уравнениям (2).

Поверхность S называется поверхностью вращения с осью d , если она составлена из окружностей, центры которых лежат на прямой d , и лежат в плоскости , перпендикулярной d .

Поверхность, состоящую из некоторого семейства параллельных прямых, будем называть цилинд­ром, прямые из этого семейства – образующими цилиндра, а линию пересечения этой поверх­ности и плоскости, не параллельной образующим, назовем направляющей этого цилиндра.

Поверхность, состоящую из прямых, проходящих через фиксированную ее точку, назовем конусом.

Линию L (поверхность ) назовем алгебраической, если в некоторой декартовой системе координат ее уравнение является алгебраическим, т.е. имеет вид

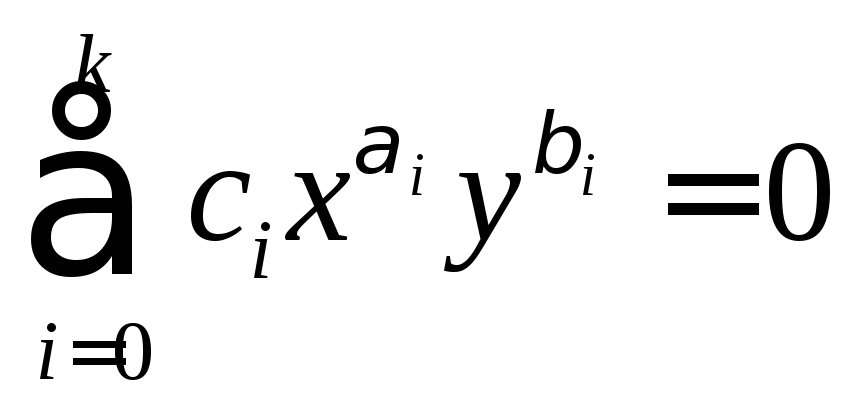
где , – действительные, a , – целые неотрицательные числа.

При этом будем называть порядком линии L (поверхности ).

Основные утверждения

Уравнение F(x,y) = 0 задает в пространстве цилиндрическую поверхность с образующей, параллельной оси OZ.

Если функция F(x,y,z) удовлетворяет условию (является однородной функцией степени n), то уравнение F(x,y,z) = 0 задает коническую поверхность с вершиной в начале координат.

Пусть в плоскости (x,z) кривая задана уравнением . Тогда уравнение поверхности, полученной вращением этой кривой вокруг оси OZ, есть .

Если в некоторой декартовой системе координат линия (поверхность) задается алгебраическим уравнением порядка п, то в любой другой декартовой системе ко­ординат ее уравнение будет алгебраическим порядка n.

Задача 51. Даны две точки и , расстояние между которыми равно . Найти множество точек, сумма квадратов расстояний от которых до точек и равна при условии, что .

Задача 52. Найти множество точек, для которых квадрат расстояния до точки пересечения двух взаимно перпендикулярных прямых в раза больше произведения их расстояний до этих прямых.

Задача 53. Вокруг точки вращается луч с постоянной угловой скоростью . По этому лучу движется точка с постоянной скоростью . Составить уравнение линии, описываемой точкой , в полярных координатах, если в начальный момент движения луч совпадает с положительным направлением полярной оси, а точка – с началом координат .

Задача 54. Написать уравнения:

1) плоскостей координат ;

2)плоскостей, проходящих через точку и параллельных плоскостям координат , , ;

3) плоскостей, делящих пополам двугранные углы между координатными плоскостями и и и .

Задача 55. Составить уравнение круглого конуса, основанием которого служит окружность , а вершина находится в точке

Задача 56. Написать уравнение поверхности, получающейся при вращении гиперболы :

1) вокруг ее действительной оси; 2) вокруг ее мнимой оси.

Задача 57. Центр окружности радиуса , плоскость которой перпендикулярна к оси , перемещается по оси с постоянной скоростью . По этой подвижной окружности равномерно перемещается точка так, что луч вращается с постоянной скоростью . Составить параметрические уравнения линии, описываемой точкой , при условии, что в начальный момент движения точка расположена на оси абсцисс.