4.4. Моделирование двухконтурной спр.

Представим модель двухконтурной СПР, построенную в программе Matlab:

Объект управления имеет вид:

---------------------------------------------------

ИССЛЕДОВАНИЕ ЭЛЕКТРОМЕХАНИЧЕСКИХ СИСТЕМ

---------------------------------------------------

ВВЕДИТЕ ТИП ИССЛЕДУЕМОЙ СИСТЕМЫ УПРАВЛЕНИЯ:

1 - СПР

2 - АКОР

3 - ОКСУ

1

--------------------------------

ВВОД БАЗОВЫХ ВЕЛИЧИН:

Введите число двигателей n=

n=2

Введите напрjaжение управления номинальное Uyn=

Uyn=10

Введите ток возбуждения номинальный ivn=

ivn=10.1

Введите напяжение возбуждения номинальное Uvn=ivn*Rv

Uvn=64

Введите максимальный ток двигателя Idmax=

Idmax=428

Введите угловую скорость двигателя номинальную wdn=

wdn=88.96

Введите конструктивную постояннную двигателя С=(Udn-idn*Rd)/wdn

C=2.5

Суммарная конструктивная постояннная равна Cs

Cs =

5

Момент максимальный Mdmax=

Mdmax =2140

-----------

ВВОД ДОПОЛНИТЕЛЬНЫХ ВЕЛИЧИН НЕОБХОДИМЫХ ДЛЯ МОДЕЛИРОВАНИЯ:

Введите величину зазора d=

d=1.57

Введите момент инерции первой массы J1s=

т.е момент инерции двигателей и редуктора

J1s=3.36

Введите момент инерции второй массы J2=

J2=33.6

момент инерции одномассовой системы

Js =

3.6960e+001

Введите эквивалентную жесткость с12=

c12s=7100

Введите коэффициент вязкого трения vz=0.01*c12

vz=71

Введите сопративление обмотки возбуждения Rv=

Rv=2.34

Введите коэффициент передачи возбудителja

Kv=Kf*Rv*ivn/Uyn

Kv=1.95

Введите коэффициент передачи генератора Kg=(Udn*n)/ivn

Kg=55

Введите постоянную времени генератора Tg=Lv/Rv

Tg=1.5

Введите коэффициент сопротивление якорной цепи Ra=

Ra=0.16

Введите постоянную времени якорной цепи Ta=La/Ra

Ta=0.061

Нажмите "1" чтобы исправить ошибку

или

Нажмите любую другую клавишу длja продолжениja

ВВЕДИТЕ ТИП ИССЛЕДУЕМОЙ СПР:

1 - техконтурная СПР

2 - двухконтурная СПР с ПИД регулятором тока

3 - пятиконтурная СПР

4 - четырехконтурная СПР

я выбираю вариант №2

------------------------------

ПАРАМЕТРЫ ДВУКОНТУРНОЙ СПР

------------------------------

kot = 2.3364e-002

kow = 1.1241e-001

kow1 = 1.1241e-001

koy = 4.6729e-003

kow2 = 1.1241e-001

ПИД-регулятор тока якорной цепи P+I/s+D*s

коэффициенты P I D соответственно равны

ans = 1.1662e+001

ans = 7.4705e+000

ans =6.8355e-001

П-регулятор скорости P

коэффициент P равен

ans = 3.8411e+001

>>

5. Косу с коррекцией питающего напряжения и оптимальной обратной связью по току якорной цепи.

Если в системе Г-Д рассмотреть контур питающего напряжения, в котором производится коррекция питающего напряжения, т.е. за счет регулятора питающего напряжения компенсируем большую постоянную времени Тг, в результате этого по быстродействию приближаем систему Г-Д к системе ТП-Д в пределах допустимого коэффициента форсировки. Чем больше коэффициент форсировки, тем быстрее происходит переходный процесс.

При введении контура питающего напряжения регулятор питающего напряжения:

Передаточная функция замкнутого контура питающего напряжения:

.

ПренебрегаяТμ получаем .

=

В результате введения контура питающего напряжения расчетная схема примет следующий вид:

Баланс напряжений якорной цепи можно записать в следующем виде:

Умножив и разделив каждую переменную на их базовое значение получим:

.

Дополнив последнее уравнение 3-мя уравнениями, описывающими w_д, М_у, w₂ получим систему уравнений:

(5.1)

Таким образом, система уравнений (5.1) – математическое описание ЭМС с приводом Г-Д.

=

Математическое описание, как следует из (6.1) представляет систему из 4-х уравнений, на одно уравнение понизили, как в системе с ЭП ТП-Д, поэтому динамика полученной системы будет приближаться к ТП-Д.

Структурная схема объекта управления (в относительных единицах) будет иметь следующий вид:

Для синтеза, а также если имеется возможность получить информацию по току якорной цепи и скорости двигателя, то ЭМС рассматривают как одномассовую, и тогда математическое описание представляет собой систему 2-х дифференциальных уравнений:

(5.2)

Система уравнений (6.2) – математическое описание системы регулирования.

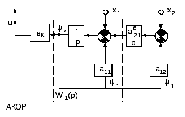
Воспользуемся вычислительной процедурой принципа максимума Л.С. Понтрягина.

Критерий оптимальности имеет вид:

Составим функцию Гамильтона:

,

где F – подынтегральная функция критерия оптимальности.

Возьмем производную функции Гамильтона по управлению и приравняем ее к нулю: .

Получим

Для того чтобы найти инеобходимо составить систему сопряженных уравнений:.

(5.3)

По системе уравнений (4.3) составляем структуру АКОР:

.

Структурная схема электропривода КОСУ по i_а, w₁:

Таким образом, получили структуру оптимального ЭП с коррекцией питающего напряжения, в котором регулятор рассчитан по методу технического оптимума и АКОР по току якоря i_а и скорости двигателя w₁. В данном виде полученная схема напоминает трехконтурную систему подчиненного регулирования (СПР) с внешним контуром скорости и подчиненным контуром тока с внутренней обратной связью.

В АКОР апериодическое звено выполняет роль регулятора тока, а интегрирующее звеновыполняет роль регулятора скорости.

Пусть математическое описание объекта регулирования представляет систему 2-х дифференциальных уравнений:

Рассмотрим влияние критерия оптимальности на величину коэффициентов оптимальных обратных связей. Синтез алгоритма оптимального управления осуществляем методом динамического регулирования. Метод динамического регулированияпредполагает дифференцируемость критерия оптимальности и уравнение Беллмана записывается в частных производных. Особенностью метода является то, что для рассматриваемого критерия оптимальности в виде АКОР (минимизация квадратичных отклонений) легко решается непосредственно задача синтеза, которая реализуется в виде линейных коэффициентов от координат системы, что позволяет получить простейший регулятор.

Критерий оптимальности:

.

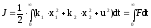Методика заключается в том, что вводится некоторая функция Беллмана: .

В общем случае уравнение Беллмана записывается в следующем виде:

(5.4)

Учитывая требования минимизации выражения в квадратных скобках по управляющему воздействию, запишем уравнение Беллмана в виде следующей системы:

(5.5)

Для нашего случая уравнение Беллмана:

Последнее уравнение можно представить в виде следующей системы:

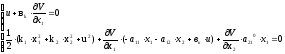(5.6)

Из 1-го уравнения: 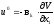(а)

Подставим его во 2-ое уравнение системы (4.6):

(5.7)

Уравнение (6.7) – оптимизированное уравнение Беллмана.

Для данного критерия доказано, что функция Беллмана ищется в виде квадратичной функции неизвестных коэффициентов.

Функция Беллмана:

С учетом того, что функция Беллмана в нашем случае ищется так:

.

Находим производные функций Беллмана по координатам:

Подставляем ив оптимизированное уравнение Беллмана:

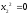Из полученного уравнения выписываем коэффициенты при, прии, получаем

(5.8)

Из второго уравнения системы (6.8) определяем значение :

D=211,4²+4*9898*0,5=64486

Подставляем найденныев 1-ое уравнение системы и находим 4 значения.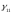

1)

D=32,6²+4*9898*0,47=19671

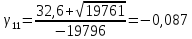
2)

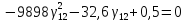
D=32,6²+4*9898*0,5=20859

Выбираем из всех значений только, т.е.;.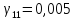

Подставляем и значенияв 3-е уравнение системы (5.8):

1) ;.

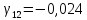2) ;.

-0,17-1,23-0,15

Выберем те значения и, которые удовлетворяют условию:

Сведем в таблицу значения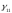,и:

---------		-----------

Таким образом

Подставим значения в уравнение (а):

ν₁ – коэффициент оптимальной обратной связи по току;

ν₂ – коэффициент оптимальной обратной связи по скорости.

V₁=2*в_к*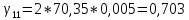

V₂=2*в_к*