Занятие 9 Плоскость в пространстве

Основные типы уравнений плоскости

Векторно-параметрическое уравнение плоскости:

. (9)

Общее уравнение плоскости:

Ax+By+Cz+D=0. (10)

Нормальное уравнение плоскости:

x cos+ycos+zcos-p = 0, (11)

где – координаты вектора единичной длины, перпендикулярного к плоскости.

Уравнение в отрезках на осях имеет вид .

Примечание: Уравнения (11) и уравнение в отрезках на осях являются частными разновидностями уравнения (10).

Основные определения

Пучком плоскостей в пространстве назовем совокупность плоскостей, проходящих через фиксированную прямую, либо попарно параллельных.

Связкой плоскостей в пространстве назовем совокупность плоскостей в пространстве, проходящих через фиксированную точку.

Пусть плоскость  параллельна двум неколлинеарным векторам и и проходит через точку с радиус-вектором . Тогда уравнение плоскости имеет вид

,

где – радиус-вектор текущей точки плоскости, u, v – числовые параметры, принимающие действительные значения.

Если плоскость  параллельна двум неколлинеарным векторам ии проходит через точкуМ(х₀, у₀, z₀), то координатно-параметрические уравнения этой плоскости имеют вид

где .

Общее уравнение плоскости имеет вид

Ах + By + Cz + D = 0,

где A²+B²+C²=0.

Если плоскость  перпендикулярна ненулевому вектору и проходит через точку, радиус-вектор которой, то уравнение этой плоскости можно представить в виде

,

где _– радиус-вектор текущей точки плоскости .

Если система координат в пространстве прямоугольная, р – расстояние от начала координат до плоскости  и  – углы между лучом, проведенным от начала координат перпендикулярно к плоскости , и осями координат OX, OY, OZ соответственно, то общее уравнение плоскости может быть записано в виде

.

Если плоскость  проходит параллельно двум неколлинеарным векто­рам и – через точку, радиус-вектор которой , то уравнение плоскости с помощью смешанного произведения векторов можно задать в виде

Если плоскость  пересекает оси OX,OY,OZ в точках (а, 0, 0), (0, b, 0) и (0, 0, с) соответственно и , то общее уравнение прямой можно записать в виде

Если в пространстве заданы точки A(x₀, y₀, z₀), B(x₁,y₁, z₁), C(x₂, y₂, z₂), не лежащие на одной прямой, то уравнение плоскости, проходящей через эти три точки, мож­но записать в виде

.

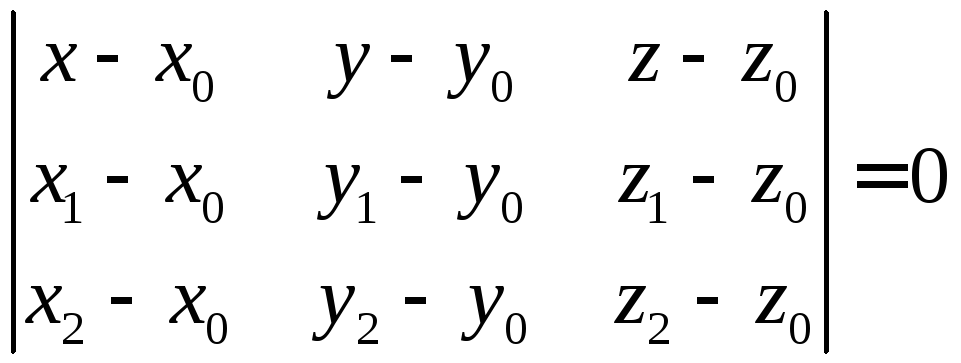Если плоскость  задана общим уравнением Ах+By+Cz+D=0, то необходимым и достаточным условием параллельности плоскости  и вектора будет следующее:

Al+Bm+Cn=0.

Плоскости _ и _, задаваемые уравнениями A₁x+B₁y+C₁z+D₁=0 и A₂x+B₂y+C₂z+D₂=0 соответственно, будут параллельны тогда и только тогда, когда существует  такое, что A₁=_, B₁=_, C₁=C_.

Если и D₁=D_, то _ и _ совпадают.

Пусть две плоскости (и) принадлежат одному пучку. Тогда любая плоскость этого пучка задается уравнением

.

Если плоскость  задана в прямоугольных координатах уравнением Ax+By+Cz+D=0, то вектор перпендикулярен к плоскости.

Примечание. Аналогичное утверждение нетрудно сформулировать относительно взаимного расположения двух точек и плоскости в пространстве.

Пусть в прямоугольной системе координат заданы уравнения плос­костей _ и _: и. Тогда наименьший из углов между плоскостями_ и _ можно определить из формулы

.

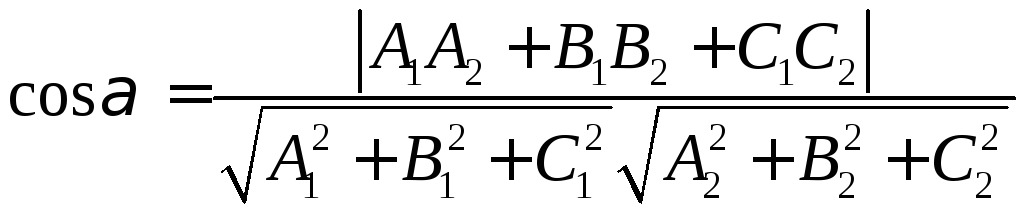Пусть в прямоугольной системе координат задан вектор и плоскость : Ax+By+Cz+D=0. Тогда угол  между вектором и плоскостью удовлетворяет уравнению

.

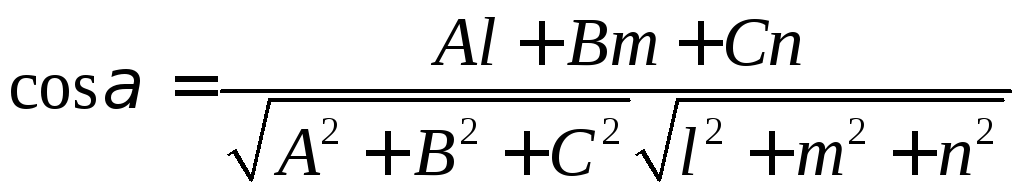Задача 74. Точка лежит в плоскости, векторимеет координаты. Доказать, что точкалежит в положительном полупространстве относительно данной плоскости.

Задача 75. 1) Зная параметрические уравнения плоскости:

, составить ее общее уравнение.

2) Зная общее уравнение плоскости , составить ее параметрические уравнения.

Задача 76. Составить уравнение плоскости, проходящей через точку и параллельной плоскости:

1)

2)

3)

4)

5) .

Задача 77. Составить уравнения плоскостей, проходящих через точку и равноудаленных от трех точеки.

Задача 78. В пучке, определяемом плоскостями инайти две перпендикулярные друг другу плоскости, одна из которых проходит через точку

Задача 79 (с решением). В прямоугольной системе координат заданы плоскости π и π

x-2y+z+4=0, 2x+y–z–7=0.

Найти уравнение биссекторной плоскости π того двугранного угла, образованного ππ, которому принадлежит точка (1,1,1).

Решение. Искомую плоскость π образуют те точки M(x,y,z), которые равноудалены от π и π и лежат в одном с точкой M квадранте,

M₀(x,y,z)

π

образованном плоскостями πи π. Расстояниеиот точкиM(x,y,z) до плоскостей πи π находятся по формулам

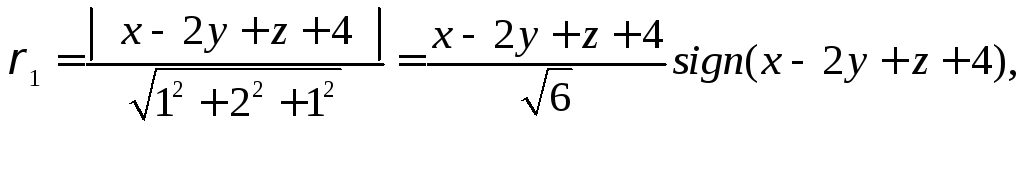
ρ=

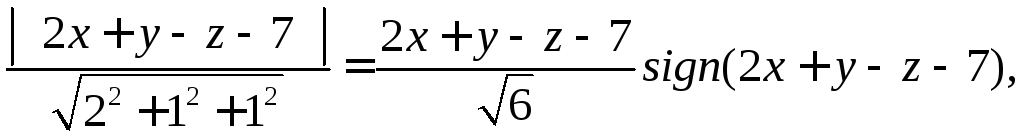
но точки М₀ и M одинаково расположены относительно плоскостей π и π₂, поэтому

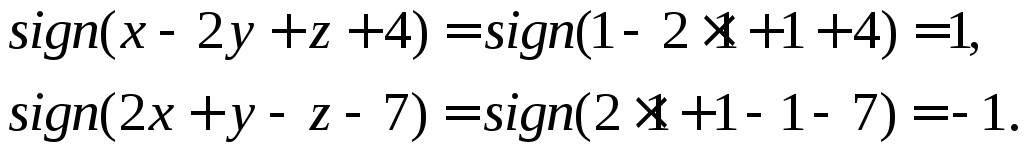
Следовательно,

ρ=, ρ=

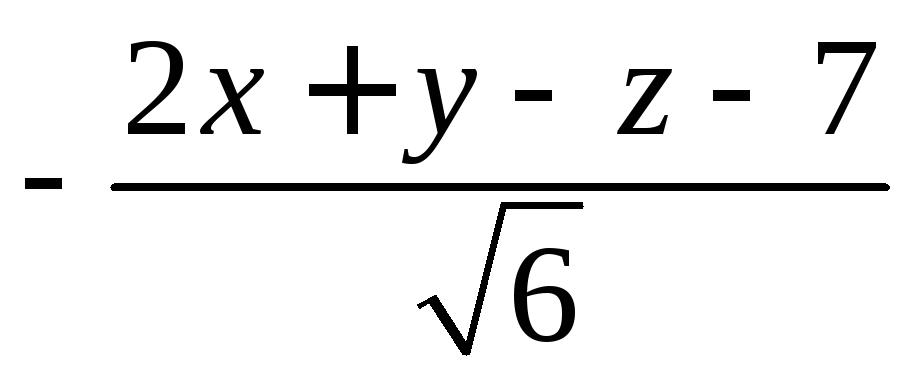
и из условия ρ= ρ получаем

3x-y-3=0.

Задача 80. Найти угол между плоскостями:

1) и

2) и

Задача 81. Составить уравнение биссекторной плоскости того двугранного угла между плоскостями ивнутри которого лежит точка