Занятие 3 Системы координат на плоскости и в пространстве

Основные определения

Будем говорить, что задана декартова система координат (на плоскости или в пространстве), если задан базис и зафиксирована некоторая точка О, называемая началом координат.

Декартовыми координатами точки М будем называть координаты вектора в указанном базисе.

Будем говорить, что нам задана полярная система координат на плоскости, если на плоскости зафиксирован некоторый луч с началом в точке О. Полярными координатами точки М плоскости будем называть пару чисел (r,) где иугол между полярной осью и радиус-вектором .

Пусть в пространстве зафиксированы плоскость , находящиеся на ней точка О и луч ОК, и ось OZ, перпендикулярная плоскости . Цилиндрическими координатами точки М будем называть упорядоченную тройку чисел где- полярные координаты ортогональной проекции точкиМ на плоскость  и z - координата на оси OZ ортогональной проекции точки М на эту ось.

Пусть в пространстве зафиксирована плоскость  с заданным на ней лучом ОК и перпендикулярный к  луч ОН. Тогда сферическими координатами точки М будем считать упорядоченную тройку чисел , где – длина радиус-вектора ,– угол между осьюОК и ортогональной проекцией на плоскость, и –угол между осьюОН и вектором .

Будем говорить, что точка С делит отрезок АВ в отношении , если АC = СВ.

Если – базис заданного множества векторов (плоскости или пространства) и – второй базис в этом же множестве, то матрицей перехода от первого ко второму базису будем называть матрицу , где есть коэффициенты разложенияэлементов второго базиса по первому базису.

Основные утверждения

Если прямоугольную декартову систему координат на плоскости выбрать согласованной с полярной, то полярные и декартовы координаты точки М будут связаны соотношениями: или

Если прямоугольную декартову систему координат в пространстве выбрать согласованной с цилиндрической, то справедливы соотношения: x = r cos, y = r sin, z = Z, где – цилиндрические координаты точкиМ.

Если декартову прямоугольную систему координат выбрать согласованной со сферической, то справедливы следующие формулы, связывающие сферические и декартовы координаты:

x =sincos, y =sinsin, z =cos,

Если точки изаданы своими координатами в декартовой системе координат, то векторимеет координаты.

Если точка делит отрезокАВ в отношении , то

Пусть в точках , радиус-векторы которыхсо­ответственно, находятся массы. Тогда радиус-вектор центра тяжести

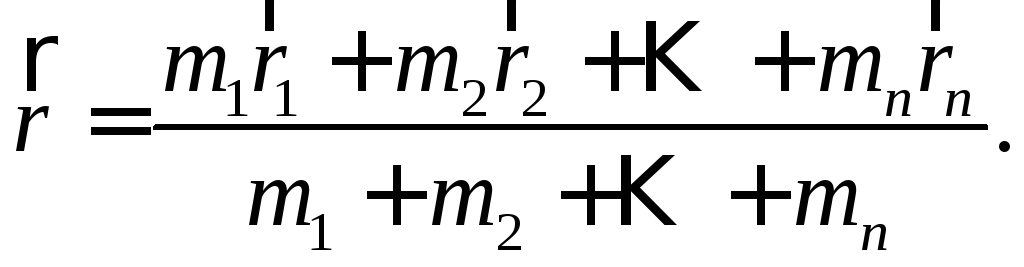
Обратно, если задан радиус-вектор центра тяжести и число точек п = 3 в случае их расположения на плоскости или п = 4 в случае пространства, то массы могут быть определены с точностью до некоторого множителяk. Отметим, что в сформулированном утверждении можно допустить и отрицательные значения чисел m_i, в этом случае центр тяжести находится вне многоугольника.

Задача 14. Дан правильный шестиугольник . Принимая за начало координат вершину, а за базисные векторыи, найти координаты вершин шестиугольника и его центра.

Задача 15. Дан параллелепипед . Принимая за начало координат вершину, а за базисные векторыи, найти координаты:

1) вершин и;

2) точек и- середин реберисоответственно;

3) точек ипересечения диагоналей гранейисоответственно;

4) точки пересечения диагоналей параллелепипеда.

Задача 16. Даны две различные точки ,. Найти координаты:

1) точки , лежащей на отрезкеи такой, что;

2) точки , лежащей на прямойвне отрезкаи такой, что.

Задача 17. [2,1.32] В точках, имеющих радиус–векторы , сосредоточены массы. Найти радиус–вектор центра тяжести этой материальной системы.

Задача 18. Один из концов отрезка находится в точке , его серединой служит точка. Найти другой конец отрезка. Система координат аффинная.

Задача 19. Даны вершины треугольника: и. Найти третью вершину, зная, что середина сторонылежит на оси, а середина сторонына плоскости. Система координат аффинная.

Задача 20. Дан правильный шестиугольник , длина стороны которого равна 1. Приняв за полюс вершину, за положительное направление полярной оси – направление вектора, а за положительное направление отсчета углов – направление кратчайшего поворота отк, определить в этой системе полярные координаты вершин шестиугольника и его центра.

Задача 21. Относительно полярной системы координат даны точки ,,,. Какие координаты будут иметь эти точки, если повернуть полярную ось вокруг полюса в положительном направлении на угол?

Задача 22. Найти прямоугольные координаты точки, лежащей на шаре радиуса 1, зная ее широту и долготу.

Задача 23. Найти цилиндрические координаты точек по их прямоугольным координатам: