B c

A D

Из рисунка видно, что имеют место соотношения

, ,, поэтому

, .

Решая эту систему, получаем, что

, ,,.

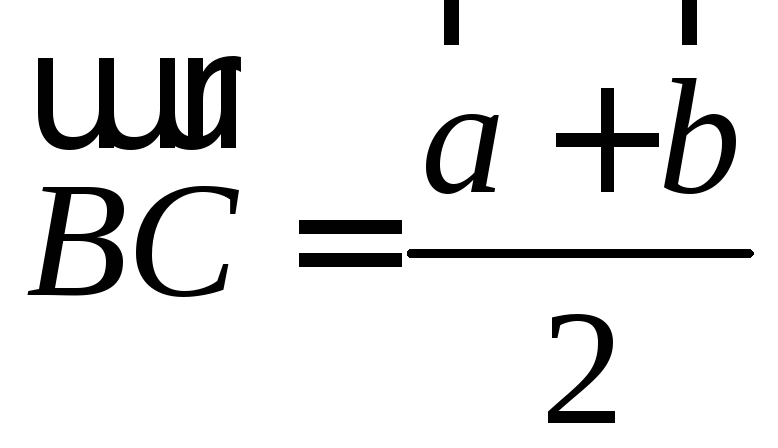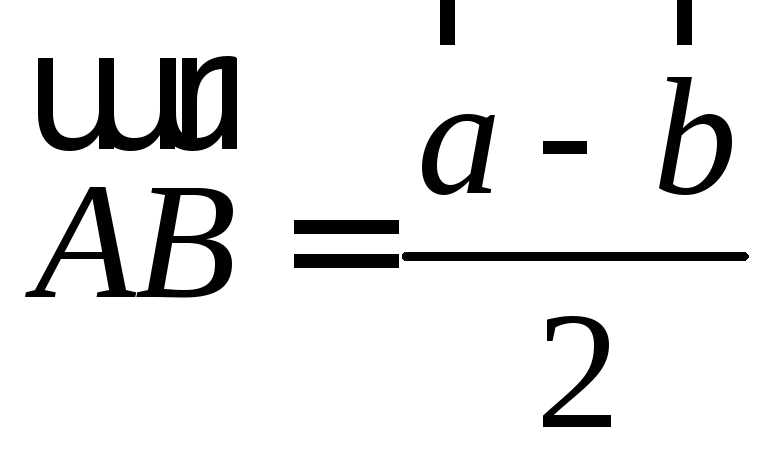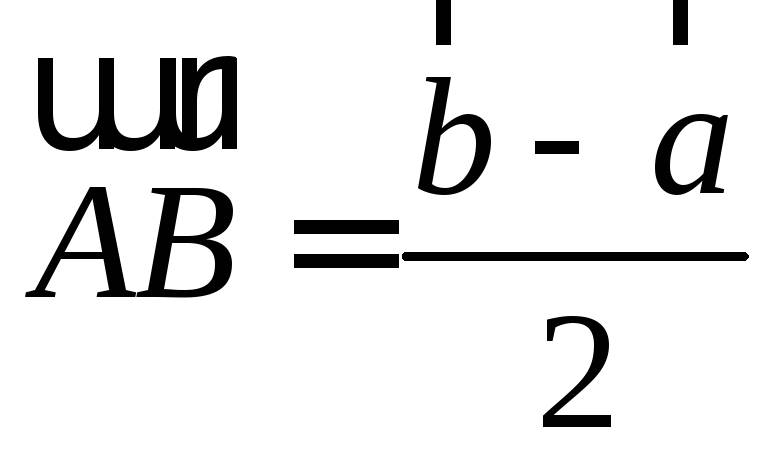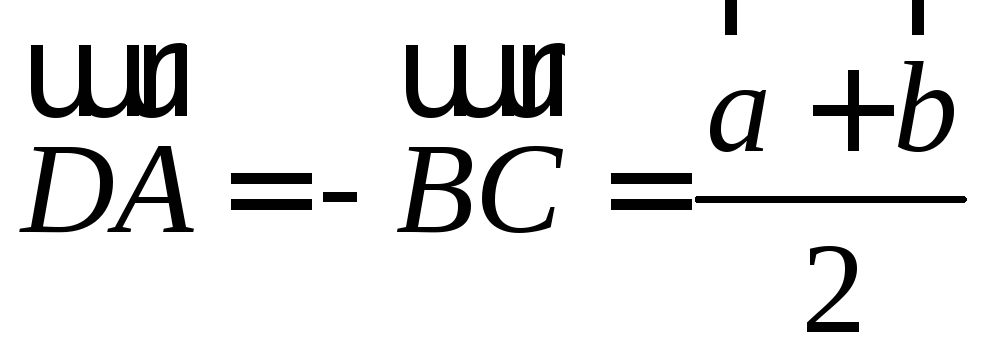Задача 2. В треугольнике проведены медианыи. Представить векторыив виде линейных комбинаций векторови

Задача 3. Точки ислужат серединами стороничетырехугольника(плоского или пространственного). Доказать, что. Вывести отсюда теорему о средней линии трапеции.

Задача 4. Точки ислужат серединами сторонипараллелограмма. Выразить векторыичерез векторыи.

Задача 5. На стороне параллелограммаотложен отрезок, а на диагонали- отрезок. Доказать, что векторыиколлинеарны, и найти отношение.

Задача 6. Из точки О выходят два вектора, и. Найти какой-нибудь вектор, идущий по биссектрисе угла.

Занятие 2 Базис, координаты векторов

Основные определения

Выражение вида будем называть линейной комбинацией векторовс коэффициентами. Если все коэффициенты линейной комбинации равны 0, то будем называть ее тривиальной линейной комбинацией.

Система векторов называется линейно зависимой, если существует некоторая нетривиальная линейная комбинация, равная нулевому вектору, и линейно независимой – в противном случае.

Система векторов называется линейно зависимой, если хотя бы один из векторов этой системы равен линейной комбинации остальных векторов.

Будем говорить, что векторы и коллинеарны, если прямые АВ и CD параллельны.

Назовем векторы ,,…, компланарными, если существует плоскость , которая параллельна одновременно всем прямымА₁B₁ , А₂B₂ ,...., А_kB_k .

Базисом на прямой назовем ненулевой вектор, лежащий на этой прямой. В некоторых случаях базисный вектор прямой будем называть направляющим вектором этой прямой.

Базисом на плоскости назовем упорядоченную пару неколлинеарных векторов.

Базисом в пространстве будем называть упорядоченную тройку некомпланарных векторов.

Если – базис совокупности векторов (пространства, плоскости или прямой) ито числаназываются координатами вектора в заданном базисе.

Примечание: Отметим, что в соответствии с определением координаты вектора в пространстве составляют упорядоченную тройку чисел, координатами вектора плоскости является упорядоченная пара чисел и координатой вектора прямой является единственное число.

Задача 7. Доказать утверждения: 1) конечная система векторов, содержащая нулевой вектор, линейно зависима; 2) конечная система векторов, содержащая два равных вектора, линейно зависима.

Задача 8. Даны три вектора . Найти координаты векторов,.

Задача 9. Проверить, что векторы иобразуют базис на плоскости. Найти координаты векторовив этом базисе.

Задача 10. Проверить, что векторы ,иобразуют базис в пространстве. Найти координаты векторов,ив этом базисе.

Задача 11. В параллелограмме точка- середина отрезкаи– точка пересечения диагоналей. Принимая за базисные векторыи, найти в этом базисе координаты векторов.

Задача 12. Дан правильный шестиугольник . Принимая за базисные векторыи, найти в этом базисе координаты векторов.

Задача 13. В треугольнике проведена биссектриса. Найти координаты векторав базисе, образованном векторамии.