.M(X,y,z)z

.

Mm

O y

X

Задача 104.( с решением) Выяснить, какие линии получаются при сечении поверхности однополостного гиперболоида

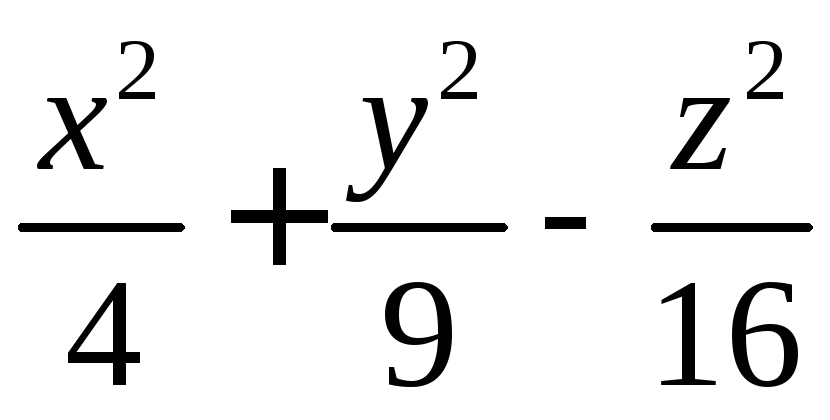
плоскостью x=const, z=const.

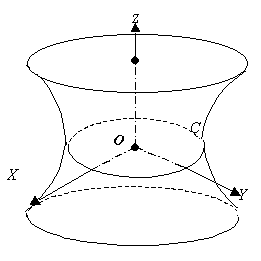
Решение. При z=const= z₀ получаем в сечении эллипс

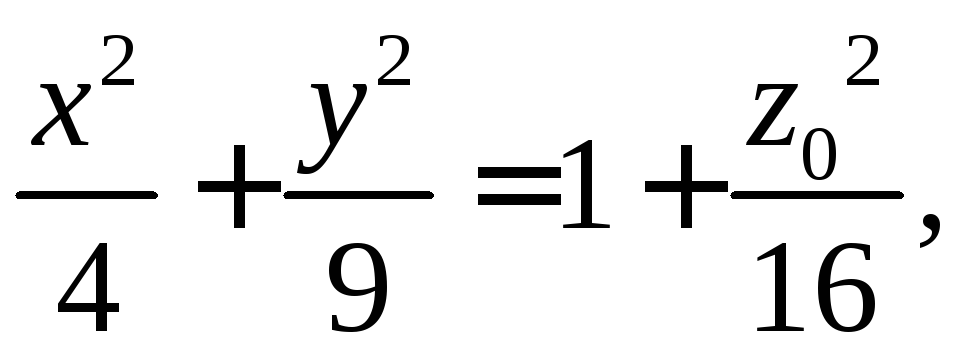
в случае z₀=0 так называемый горловой эллипс

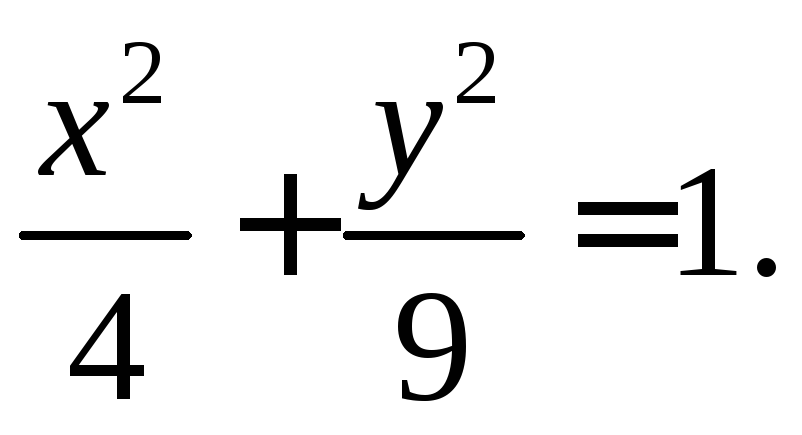
Рассмотрим теперь сечение плоскостью x=const=x₀.Если , то получаем гиперболу с действительной осьюOY

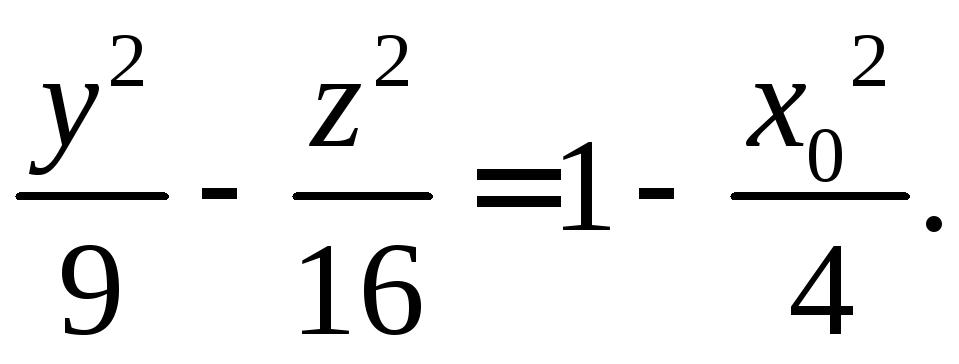
. При x₀=2 получаем уравнение двух прямых., целиком лежащих на поверхности гиперболоида

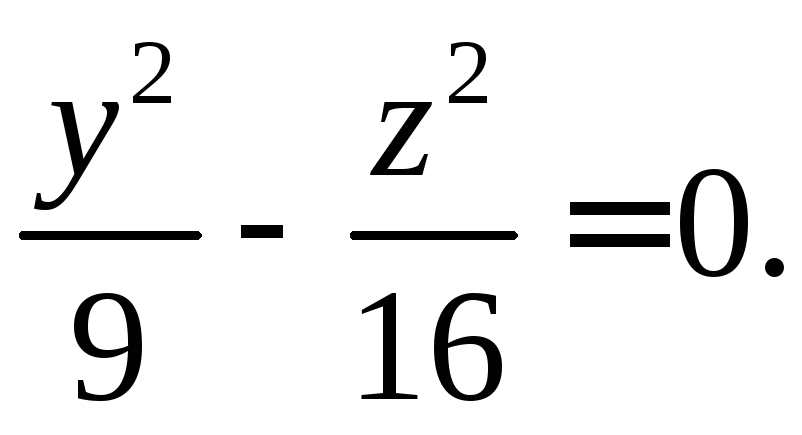
Если , то имеем гиперболу с действительной осьюOZ

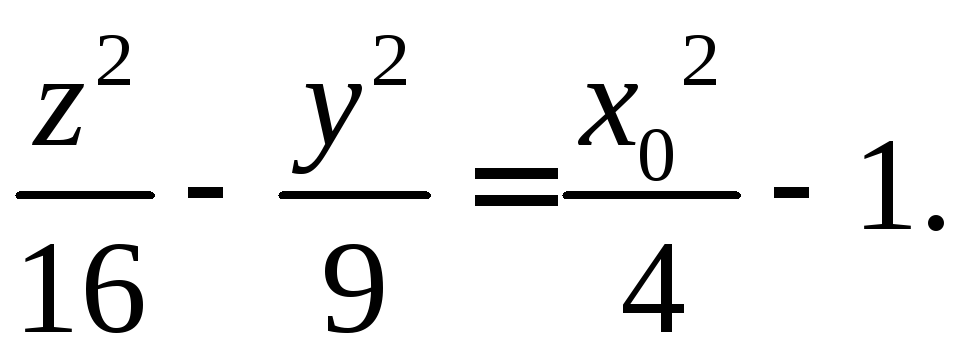
Примечание. В случае, если плоскость координат не параллельна координатной плоскости, для определения вида кривой второго порядка, получающейся в сечении, надо перейти в прямоугольную систему координат, связанную с секущей плоскостью.

Задача 105. Написать уравнение сферы:

1) с центром в точке и радиусом;

2) с центром в точке и радиусом 1.

Задача 106. Найти ось вращения поверхности, изобразить поверхность

Задача 107. Найти уравнение поверхности, получаемой вращением параболы

1) вокруг оси ; 2) вокруг оси

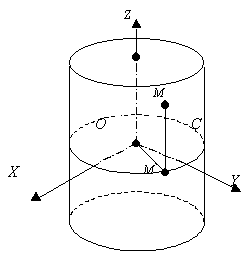
Задача 108. (с решением) Доказать, что уравнение в декартовой прямоугольной системе координат является уравнением прямой круговой цилиндрической поверхностис образующими, параллельными осиOZ, причем плоскость XOY пересекает эту поверхность по окружности C радиуса a с центром в начале координат.

Решение. В самом деле, координаты точки M(x,y,z) удовлетворяют уравнению тогда и только тогда, когда координатыпроекции точкиM на плоскость XOY удовлетворяют этому уравнению, а это значит, что точка M лежит на поверхности, заданной уравнением тогда и только тогда, когда ее проекцияна плоскостьXOY лежит на окружности C .

Значит, есть уравнение цилиндрической поверхности,

описанной выше.

Задача 109. Найти уравнение прямого кругового цилиндра радиуса с осью

Задача 110. Найти уравнение конуса с вершиной в точке касающегося сферы.

Задача 111. Найти уравнение конуса с вершиной в точке и направляющей – окружностью.

Задача 112. Найти прямолинейные образующие параболоида , пересекающиеся в точке.

Задача 113. Найти центр и радиус окружности

Задача 114. ( с решением). Выяснить, какие линии получаются при сечении поверхности однополостного гиперболоида

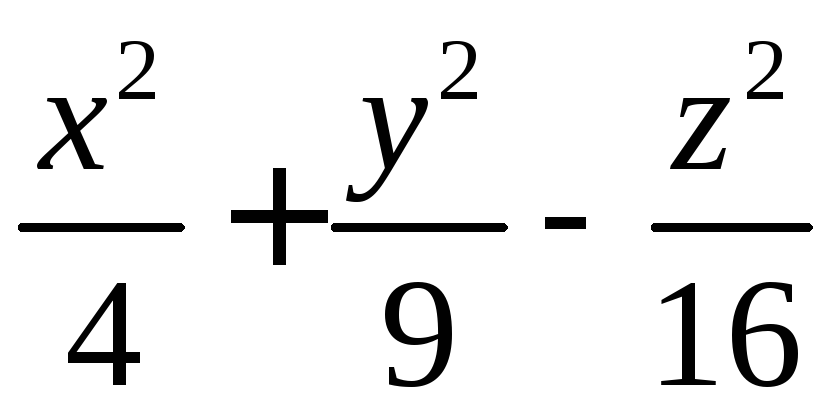
плоскостью x=const, z=const.

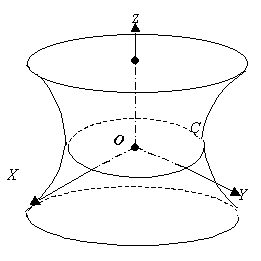
Решение. При z=const= z₀ получаем в сечении эллипс

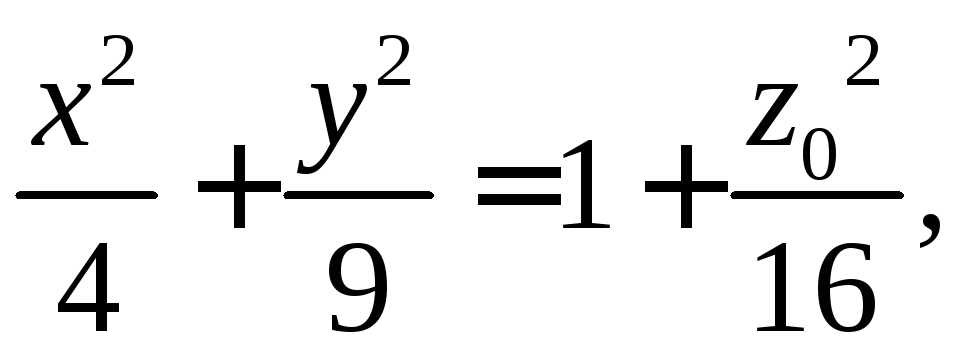
в случае z₀=0 так называемый горловой эллипс

Рассмотрим теперь сечение плоскостью x=const=x₀.. Если , то получаем гиперболу с действительной осьюOY

. При x₀=2 получаем уравнение двух прямых., целиком лежащих на поверхности гиперболоида

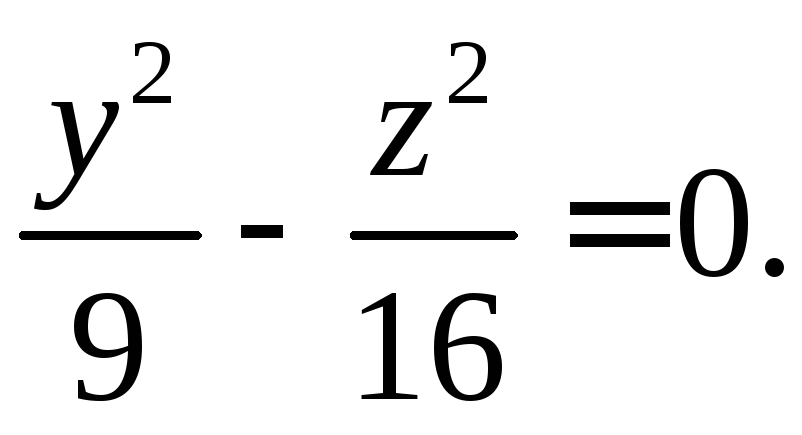
Если , то имеем гиперболу с действительной осьюOZ

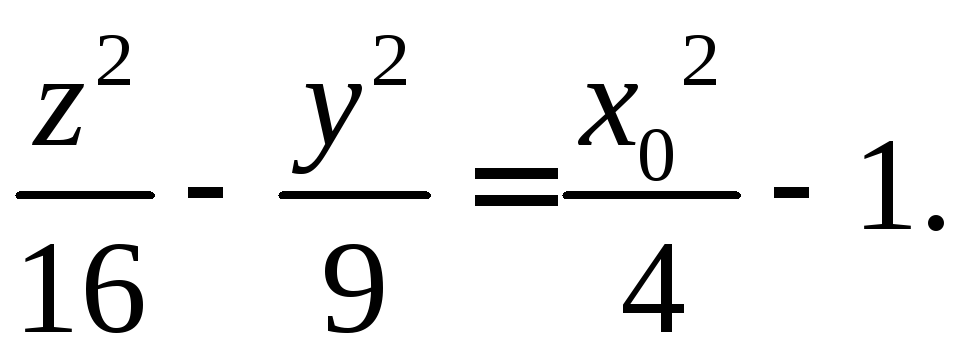
Примечание. В случае, если плоскость координат не параллельна координатной плоскости, для определения вида кривой второго порядка, получающейся в сечении, надо перейти в прямоугольную систему координат, связанную с секущей плоскостью.

Модуль IV занятие 14 Преобразования плоскости

Основные определения

Отображение множестваX в множество У – это правило, которое каждому элементу сопоставляет единственный элемент, называемый образом элемента х при отображении . МножествоX называется областью определения, а множество У - областью значений отображения . Совокупностьf(X) образов всех элементов называется множеством значений отображенияf (образом множества X при отображении f).

Отображение называется преобразованием множестваX. Ограничением отображения на подмножественазывается отображениесовпадающее сf на М.

Отображение называется вложением (или инъективным отображением), если изследуетОтображениеf называется наложением (или сюръективным отображением), если . Отображениеf называется взаимно однозначным отображением X на Y (или биективным отображением), если оно является вложением и наложением.

Произведением отображений иназывается отображение, определяемое равенством. Произведениеgf определено, если множество значений отображения f входит в область определения отображения g.

Тождественное преобразование i множества X определяется равенством i(x) = х для любого элемента .

Отображение называется обратным к отображениюи обозначается, если для любых,справедливы равенства. Обратное отображение существует, еслиf является взаимно однозначным: , гдех - единственный элемент из X, такой, что f(x) = y.

Прообразом элемента (в геометрии - точки) при отображенииназывается любой элементтакой, чтоf(x) = y. Полным прообразом множестваназывается совокупность всех прообразов всех элементов изS.

Точка называется неподвижной точкой преобразования, еслиf(x) = х. Множество называется неподвижным относительно преобразованияf, если все его точки неподвижны. Множество M называется инвариантным относительно преобразования f, если для любой точки . также. Любое неподвижное множество инвариантно, обратное неверно.

В задачах этого занятия угол поворота плоскости при заданном базисе на плоскости отсчитывается в направлении кратчайшего поворота от первого базисного вектора ко второму.

Задача 114. Дано линейное преобразование числовой прямой , (a,b – действительные числа). Доказать, что

1) f взаимнооднозначно тогда и только тогда, когда ;

2) f сохраняет направление векторов на прямой при и меняет на противоположное при.

3) при образом интервала длины является интервал длины .

Задача 115. Написать формулу, задающую линейное преобразование интервала на интервалчисловой прямой.

Задача 116. Преобразование f плоскости задано в прямоугольной системе координат формулами: .

1) Является ли преобразование f а): наложением; б): взаимно однозначным?

2) Найти полный прообраз произвольной точки плоскости .

Задача 117. Написать формулу, задающую линейное отображение интервала (a,b) на интервал (с, д) числовой прямой.

Задача 118. Найти радиус-вектор образа произвольной точки М(г) при данном преобразовании плоскости:

1) гомотетия с центром в точке и коэффициентом]

2) центральная симметрия относительно точки ;

3) параллельный перенос на вектор ;