Основные теоретические сведения и примеры решения типовых задач Тема 1 Числовые ряды.

1. Основные определения. Свойства сходящихся рядов. Необходимый признак сходимости

Напомним:

Числовой последовательностью называется множество чисел, перенумерованных с помощью натуральных чисел и расположенных в порядке возрастания номеров, т.е.

Примерами числовых последовательностей являются известные из школьного курса:

арифметическая прогрессия

,

где а – первый член прогрессии , – разность прогрессии;

а так же бесконечная геометрическая прогрессия

,

где а–первый член прогрессии, q – знаменатель прогрессии.

Последовательность считается заданной, если известен закон, по которому можно вычислить любой её член при заданномп.

Например, для арифметической прогрессии п-й член определяется по формуле для любого, для геометрической прогрессии формула общего члена.

Если , то её первый член, второй –, и т.д., а сама последовательность имеет вид:

,…

Пусть задана некоторая бесконечная последовательность чисел:

Выражение вида называютчисловым рядом и обозначают

=.

Числа называютчленами ряда, а выражение –общим или п-ным членом ряда.

Примеры рядов:

• , здесь =;

• , здесь =;

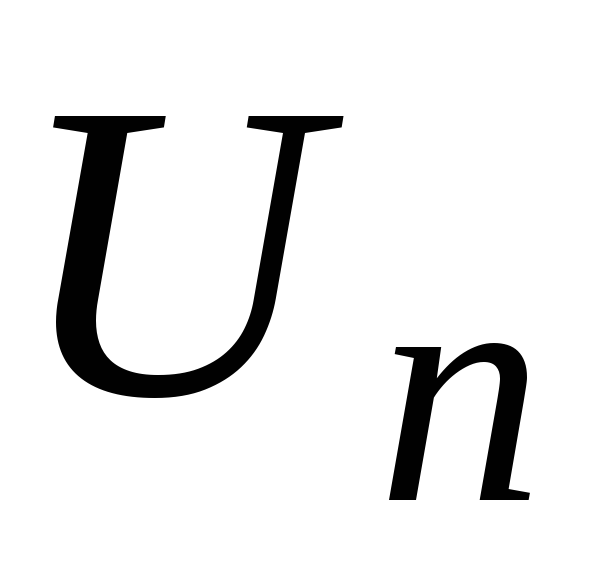• Ряд геометрической прогрессии со знаменателем , здесь=.

Сумма первых п членов числового ряда называется п-ой частичной суммой и обозначается S_n.

.

Таким образом, частичные суммы сами образуют числовую последовательность.

Если существует конечный предел последовательности п-ых частичных сумм числового ряда, равный S, т.е.

,

То числовой ряд называется сходящимся, а число S – суммой ряда.

Пример 1

Используя определение, исследовать сходимость ряда:

а) ,

б) .

Решение.

а) Рассмотрим последовательность частичных сумм данного ряда:

.

Очевидно, S_n принимает значения 1 , если число слагаемых нечетное, и значение 0, если число слагаемых четное. Такая последовательность частичных сумм предела не имеет, следовательно, ряд расходится.

б) Рассмотрим последовательность частичных сумм ряда :

Для упрощения вычислений таких сумм заметим, что общий член данного ряда

есть правильная рациональная дробь и её можно разложить на простейшие дроби. Выполнив это разложение, получим

,

т.е. каждое слагаемое частичных сумм данного ряда можно записать в виде разности двух дробей:

Тогда

Найдем предел последовательности частичных сумм:

.

Таким образом, последовательность частичных сумм имеет конечный предел, значит, ряд сходится и его сумма равна .

Пример 2.

Исследовать сходимость ряда .

Решение.

Данный ряд составлен из членов бесконечной геометрической прогрессии с первым членом а (а0) и знаменателем q.

Из школьного курса математики известно, что сумма первыхп членов геометрической прогрессии находится по формуле

.

Найдем предел частичных сумм данного ряда:

.

Величина этого предела зависит от значения q. Действительно:

1) если , тои тогда

,

следовательно, существует предел частичных сумм и значит, ряд сходится, а его сумма равна ;

2) если тои тогда

,

Значит, в этом случае ряд расходится, и суммы не имеет;

3) если q =1, то ряд принимает вид

В этом случае и, следовательно, ряд расходится;

4) если q = –1, то ряд принимает вид

.

При этом

В таком случае не существует и следовательно, ряд расходится.

Итак, можно сделать вывод, что ряд геометрической прогрессии

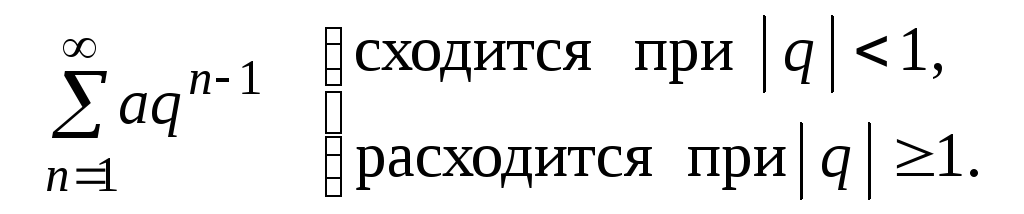
В качестве примера можно привести ряд , который сходится, поскольку, и ряд, который расходится, так как(в обоих случаях,а=1).

Основные свойства числовых рядов

1. Если сходится ряд , то сходится и ряд, полученный из данного отбрасыванием первых п членов.

Ряд называютп-ым остатком ряда и обозначают .Из сходимости остатка ряда следует сходимость самого ряда.

Иными словами, отбрасывание конечного числа членов ряда или добавление конечного числа членов не влияет на сходимость (расходимость) ряда (сумма сходящегося ряда при этом, конечно, меняется)

2. Если ряд сходится и его сумма равна S, то . Отсюда следует, что

1) при достаточно большом п ;

2) есть погрешность, допускаемая при замене суммы S ряда его п-ой частичной суммой S_п.

3. Если сходится ряд и его сумма равнаS, то ряд также сходится, причем его сумма равна. Если рядрасходится, то для любогорасходится и ряд.

4. Если ряды исходятся и имеют суммы соответственнои, то рядтакже сходится и его сумма равна.

При исследовании рядов одним из основных вопросов является вопрос о том, сходится ли данный ряд или расходится. Ответить на этот вопрос можно, конечно же, используя определение, но часто это приводит к сложным вычислениям (пример 1,б). Однако существуют условия, при выполнении которых достаточно просто ответить на вопрос о сходимости ряда. Эти условия налагаются на п-й член ряда и называются признаками сходимости. Ниже мы рассмотрим достаточные признаки сходимости, а также рассмотрим необходимый признак сходимости числового ряда (т.е. условие, при невыполнении которого ряд расходится).

Теорема (необходимый признак сходимости)

Если ряд сходится, то его общий член стремится к нулю при стремлении п к бесконечности, т.е.

.

Доказательство.

По условию теоремы ряд сходится, следовательно, по определению сходящегося ряда.

Легко видеть, что , тогда. Отсюда

,

что и требовалось доказать.

Признак является необходимым для любого ряда, но не является достаточным, т.е. из того, что п-ый член ряда стремится к нулю с увеличением п не следует сходимость самого ряда. Например, известно, что гармонический ряд является расходящимся, хотя для него выполняется условие.

Из необходимого признака сходимости следует достаточный признак расходимости (для всякого ряда):