Свойства сходящихся степенных рядов
Рассмотрим степенной ряд
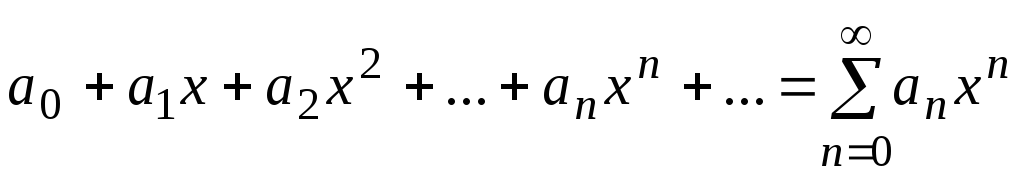
Для него справедливо
1. Сумма степенного ряда непрерывна в интервале сходимости ряда.
2. Степенной ряд можно почленно дифференцировать в интервале сходимости, т.е.
- сумма ряда S(х) дифференцируема в интервале сходимости;
- ряд, составленный из производных членов ряда
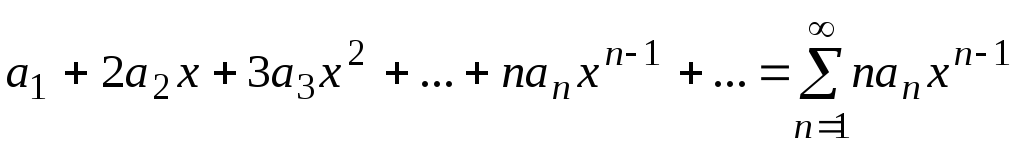
сходится в интервале сходимости исходного ряда, причем его сумма
равна S(х).
3. Степенной ряд
можно почленно интегрировать по любому
отрезку
,
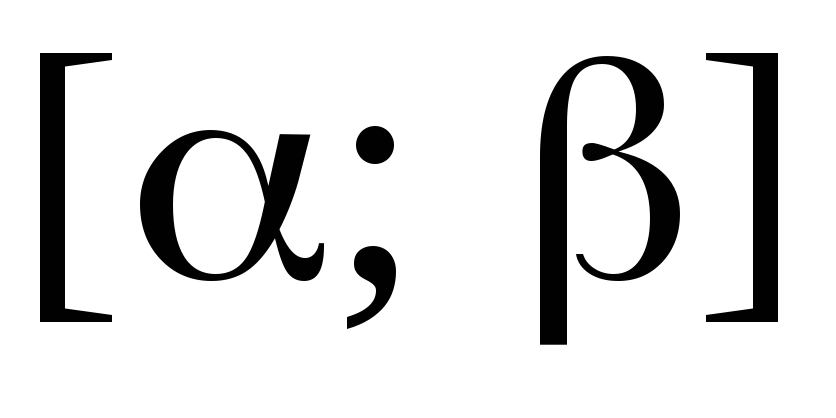принадлежащему интервалу сходимости,
т.е.
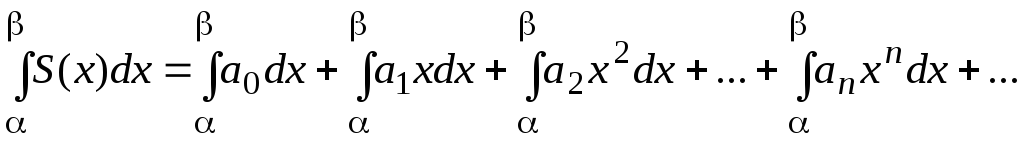
В частности,
очевидно, что степенной ряд
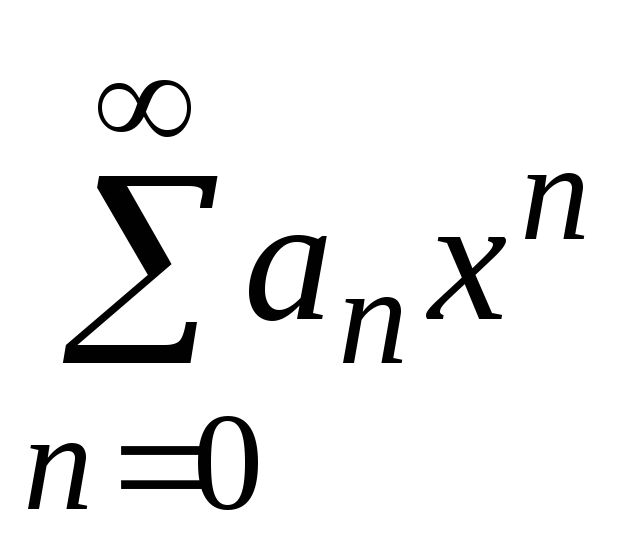можно почленно
интегрировать по отрезку [0,х]
для любого
х из
интервала сходимости ряда. При этом
получим
.
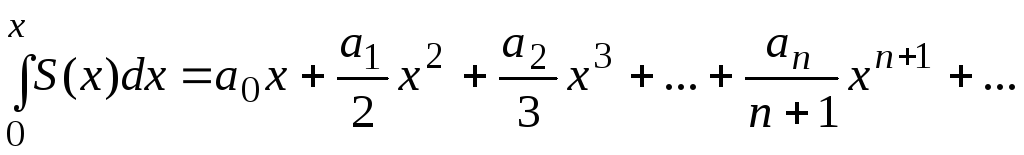Заметим, что ряды, полученные из данного степенного ряда почленным дифференцированием или интегрированием, являются так же степенными рядами, сходящимися в том же интервале, что и исходный ряд.
Из приведенных свойств следует, что степенной ряд в интервале сходимости можно почленно дифференцировать любое число раз, причем получающиеся при этом ряды имеют тот же интеграл сходимости, а суммы соответственно равны S'(х), S"(х), S"(х),.... Аналогичное утверждение можно сформулировать для почленного интегрирования ряда.
Пример 22
Найти сумму ряда
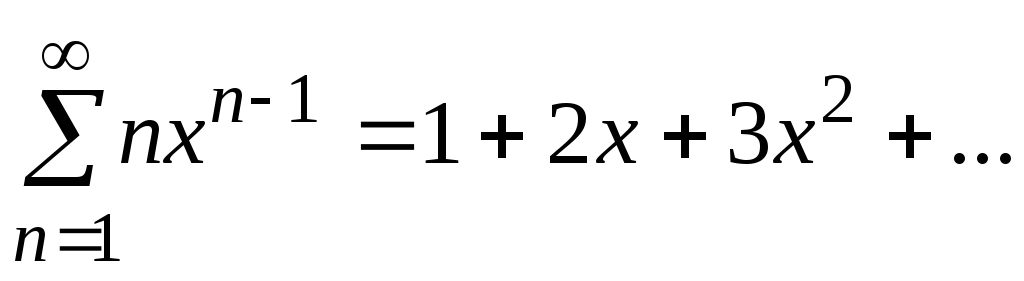
Решение.
Данный ряд является степенным по степеням х, центр сходимости х0=0, числовой коэффициент ап = п. Найдем радиус и интервал сходимости ряда:
,
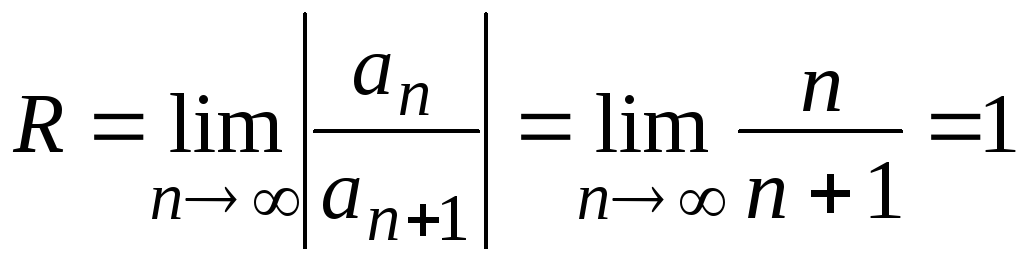следовательно, интервал сходимости х (–1;1).
Обозначим за S(х) сумму данного ряда и проинтегрируем ряд почленно по отрезку [0; x] для любого х из интервала сходимости ряда:
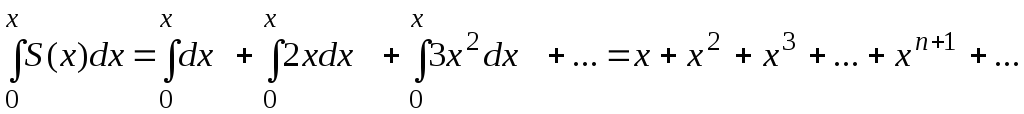
Полученный ряд составлен из членов бесконечной геометрической прогрессии со знаменателем q= х и первым членом а= х.
Нам известно, что
при знаменателе |q|<1
сумма
бесконечной геометрической прогрессии
.
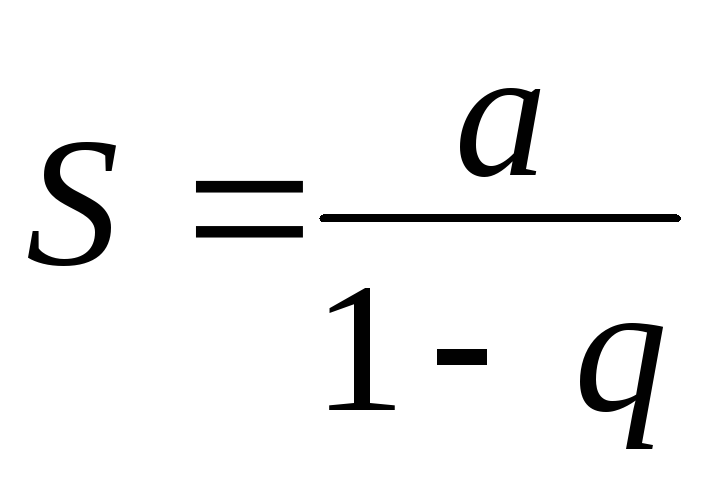Таким образом, при |х|
< 1
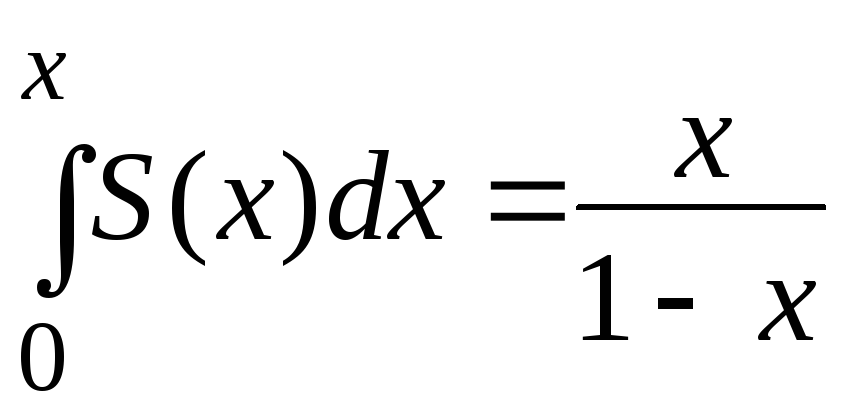
Чтобы найти искомую сумму ряда S(х), необходимо продифференцировать полученное равенство
.
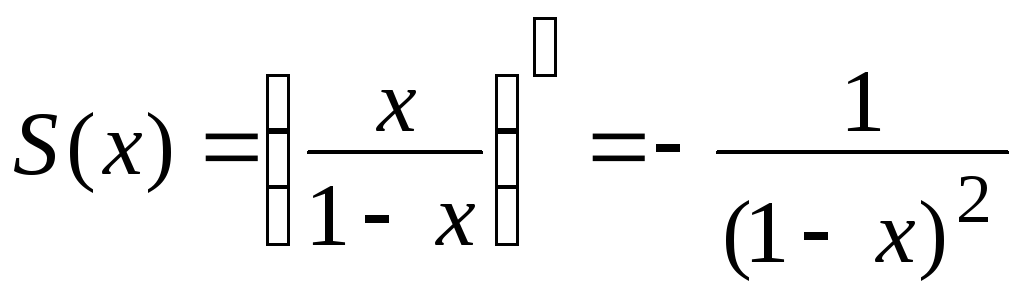Итак, внутри
интервала сходимости степенной ряд
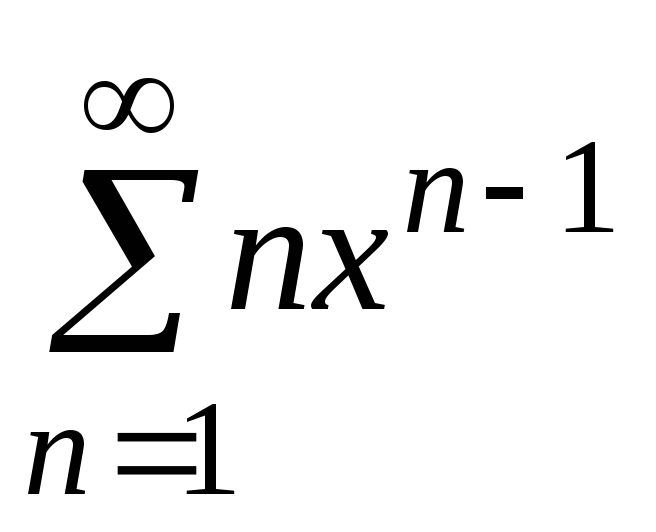сходится
к функции
,
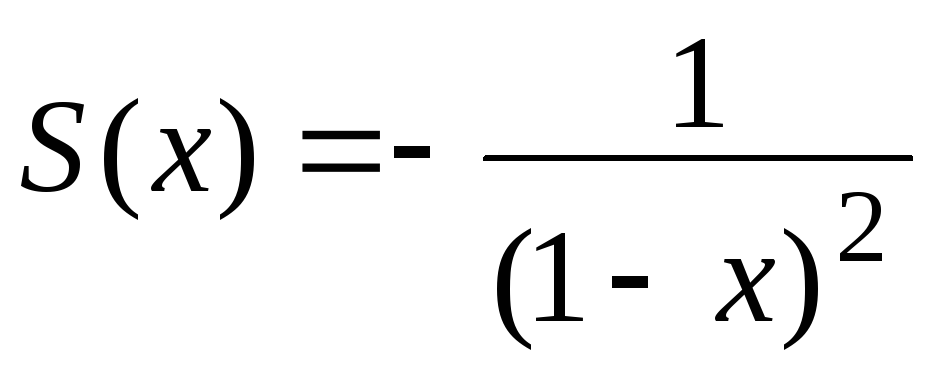т.е.
=
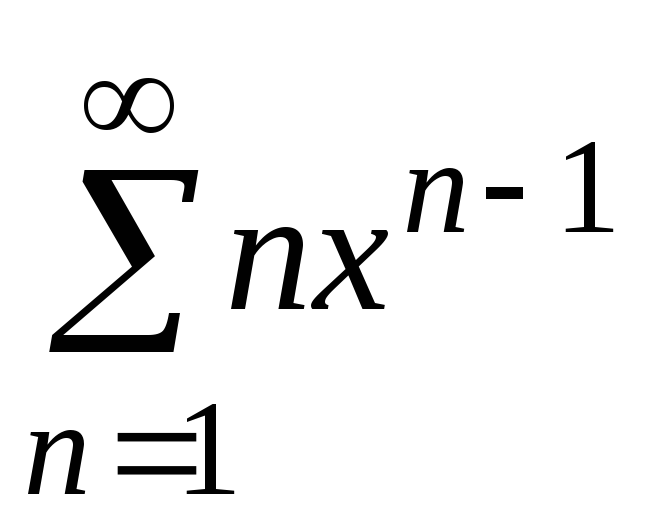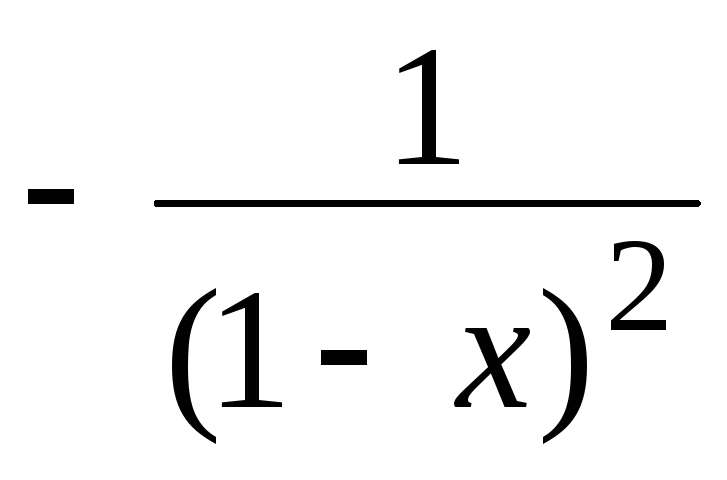для х
(–1;1).