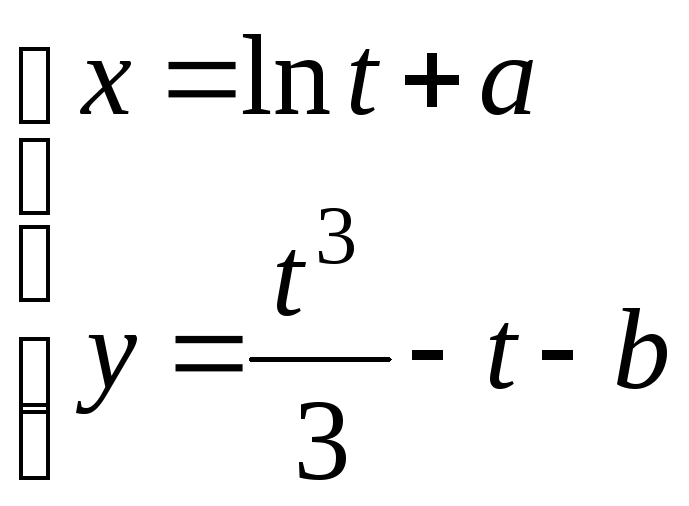- •, Найти у(0)
- •Найти у(п):
- •, Найти у(1)
- •, Найти у(0)
- •31. Найти у(п):
- •, Найти у(1)
- •31. Найти у(п):
- •, Найти у(–1)
- •31. Найти у(п):
- •31. Найти у(п):
- •, Найти у(1)
- •, Найти у(–1)
- •31. Найти у(п):
- •, Найти у(1)
- •, Найти у(0)
- •31. Найти у(п):
- •, Найти у(1)
- •, Найти у(-1)
- •, Найти у(1)
- •, Найти у(0)
- •31. Найти у(п):
- •, Найти у(1)
- •, Найти у(0)
- •31. Найти у(п):
- •, Найти у(1)
- •, Найти у(0)
- •31. Найти у(п):
- •31. Найти у(п):
- •, Найти у¢(1)
- •, Найти у¢(0)
- •Найти у(п):
- •, Найти у¢(1)
- •31. Найти у(п):
- •, Найти у¢(–1)
- •31. Найти у(п):
- •, Найти у¢(–1)
- •Найти у(п):
- •, Найти у¢(1)
- •, Найти у¢(–1)
- •Найти у(п):
- •, Найти у¢(1)
- •, Найти у¢(–1)
- •Найти у(п):
- •, Найти у¢(1)
- •, Найти у¢(0)
- •Найти у(п):
- •, Найти у¢(1)
- •, Найти у¢(0)
- •31. Найти у(п):
Вариант 1
Найти производную первого порядка функции у(х):
-
у = х7 +3х5 +
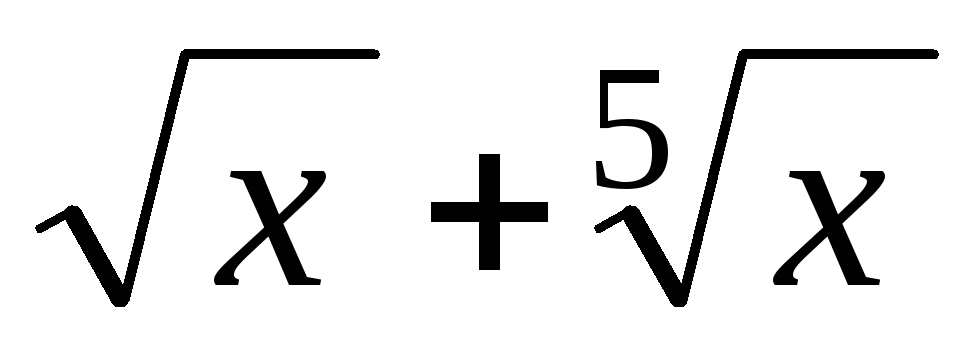 ,
найти у(1)
,
найти у(1) -
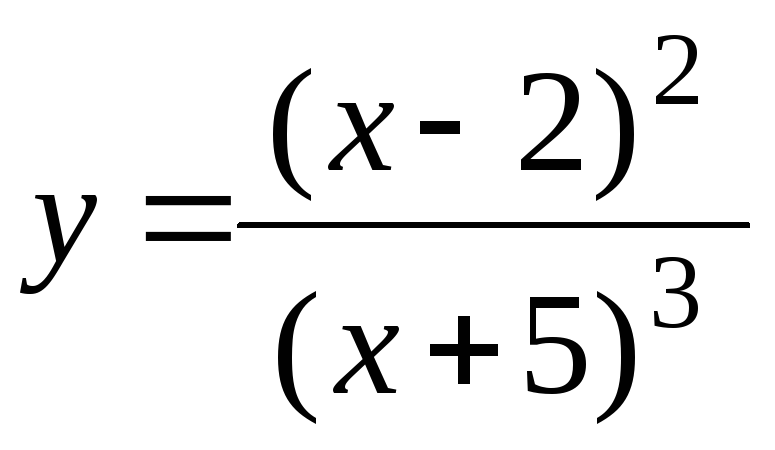 ,
найти у(0)
,
найти у(0) -
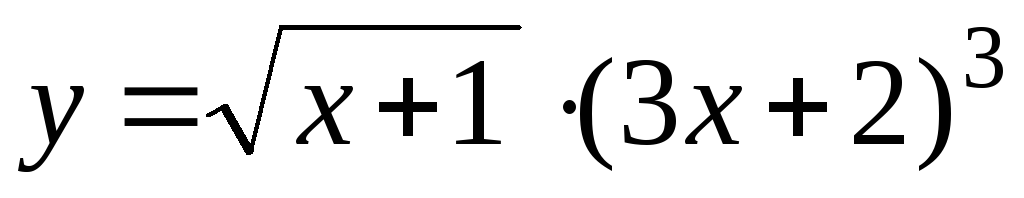 +
5
+
5 -
у = tg(x2+1)sin(x3+5)
-
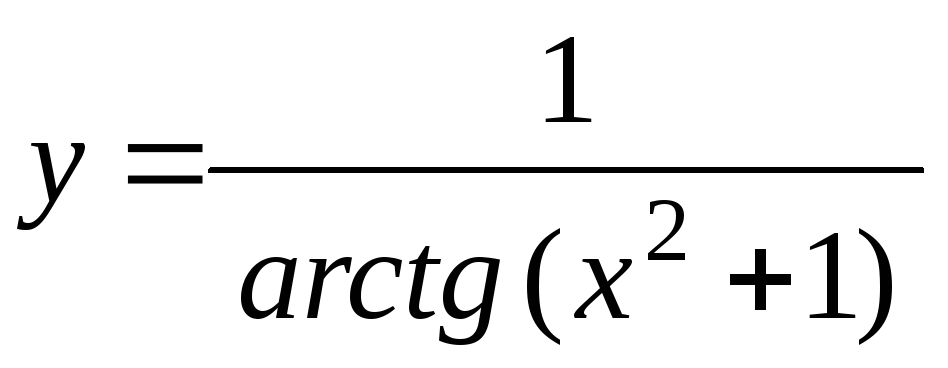
-
y=sin(5cosx) – 4tg54o
-
y = arcsin
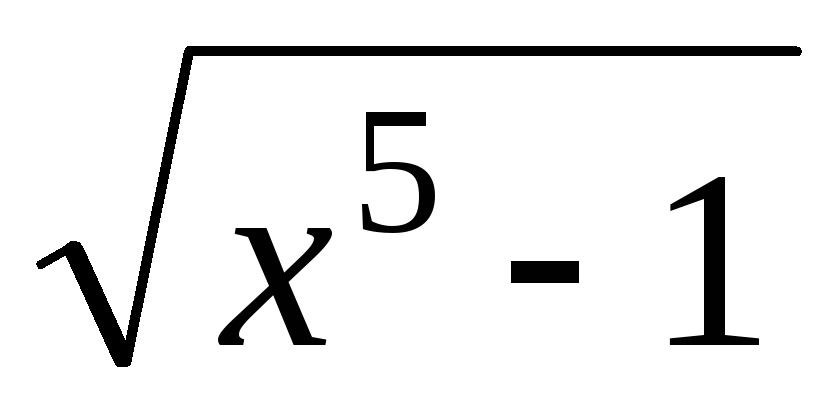 + 2+1
+ 2+1 -
y = (x+8)3tg2x
-
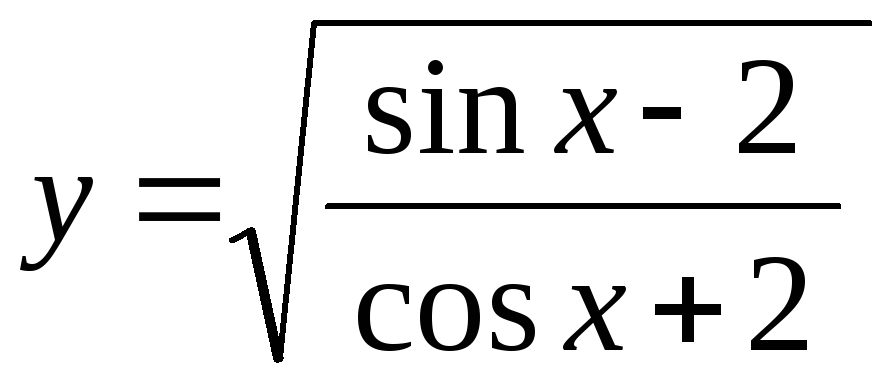 –
–
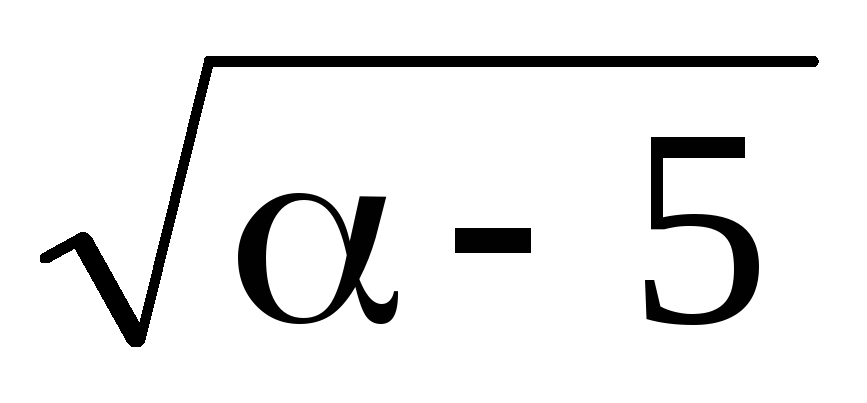
-
y = arctg3(ctgx)
-
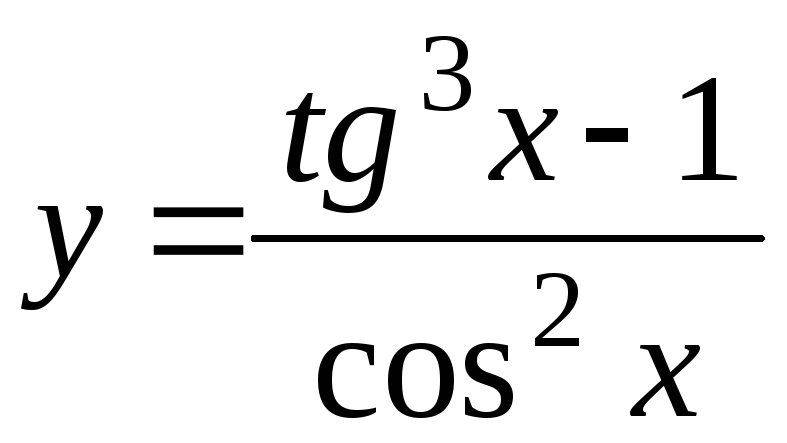
-
y= (1+cos5x)3 – 3sin4a
-
y = etgx
-
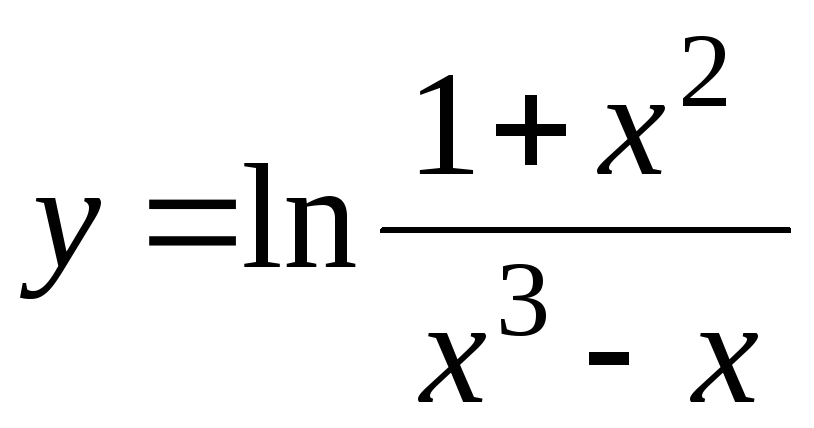
-
y = ln(sinx + cos5x)
-
у =

-
у = ln(arcctgx +
 )
) -
y = arccos(
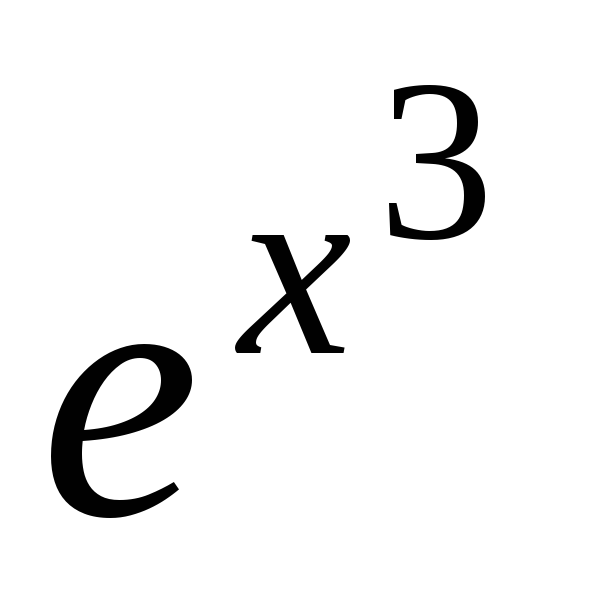 )
+ e9
)
+ e9 -
 +6lg7
+6lg7 -
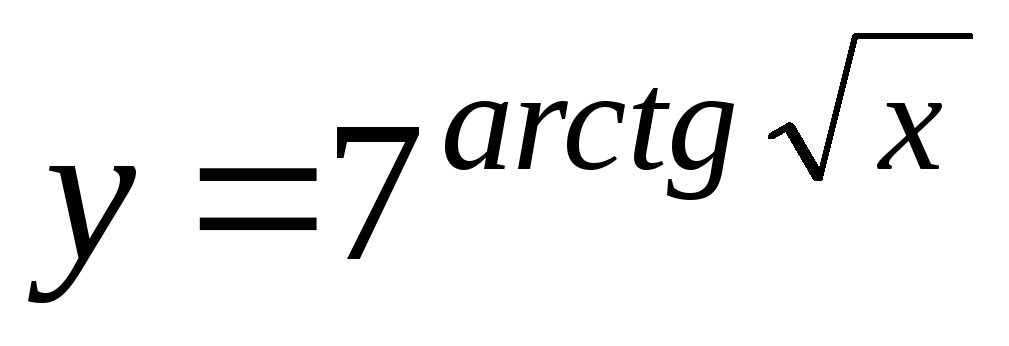
-
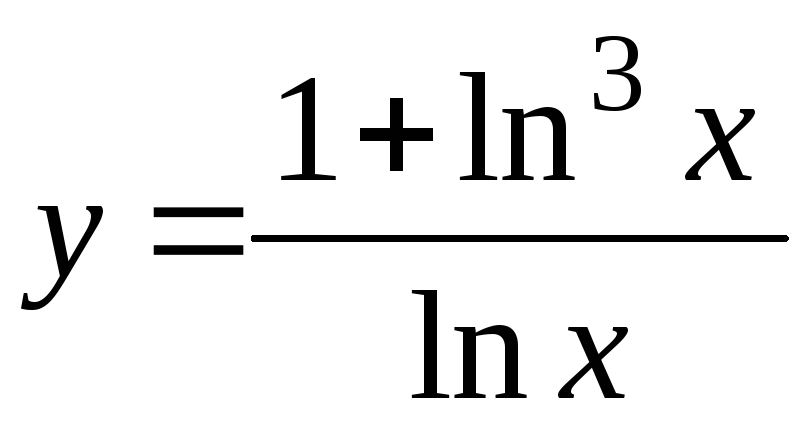
-
y =

-
y = (arcsinx)x
-

Найти производную функции, заданной неявно:
25. xey + 2x + siny –0,5= 0, найти у(0) 26. secxy + lny + x2 = 1
Найти
![]() и
и
![]() :
:
27.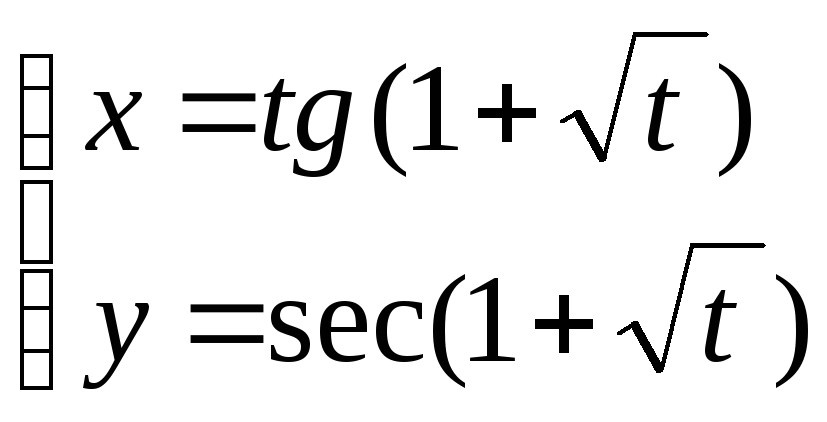 29.
29.

28.
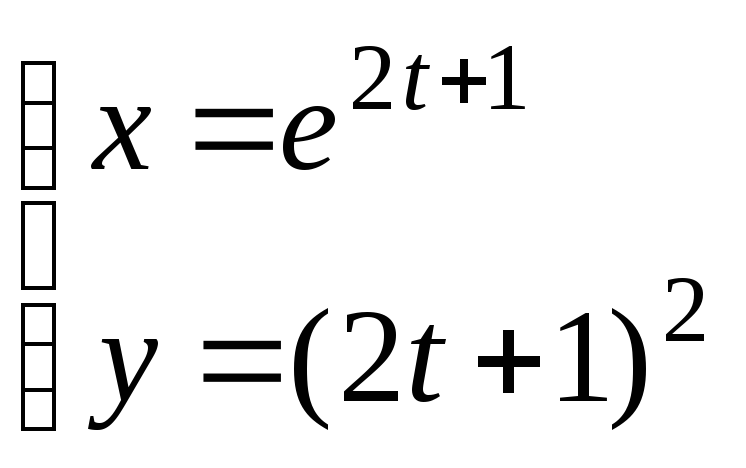 30.
30.

Найти
у(п):
![]()
Вариант 2
Найти производную первого порядка функции у(х)
-
у =
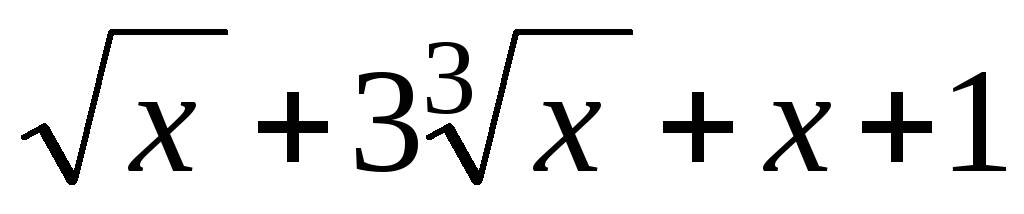 ,
найти у(1)
,
найти у(1) -
у =
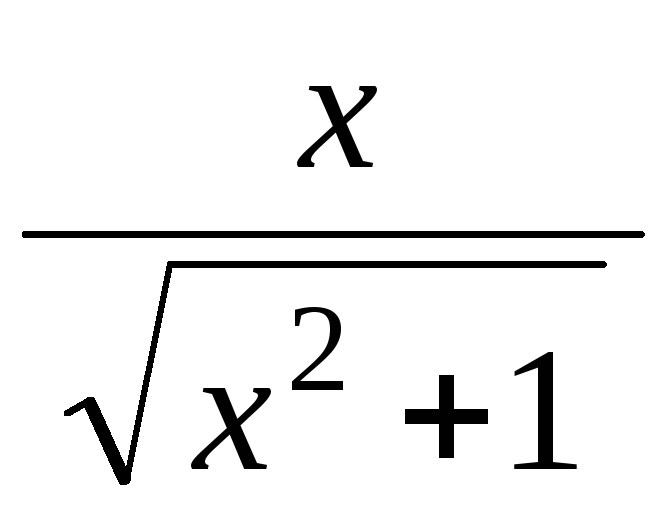 ,
найти у(0)
,
найти у(0) -
у = (5+х)8(х +
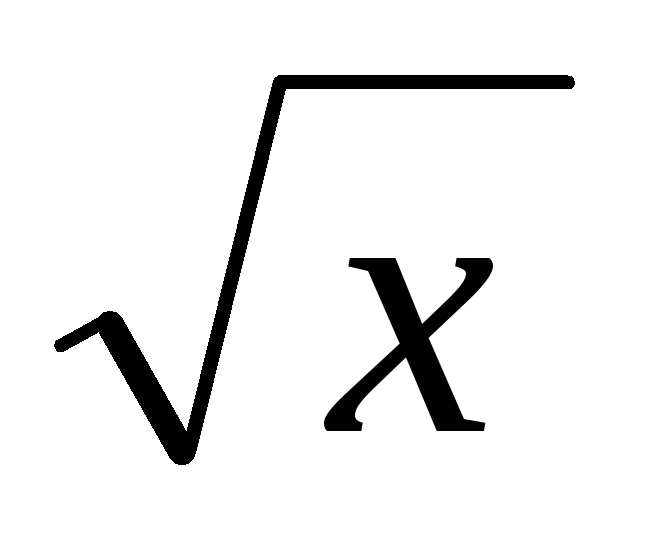 )
) -
у = tg
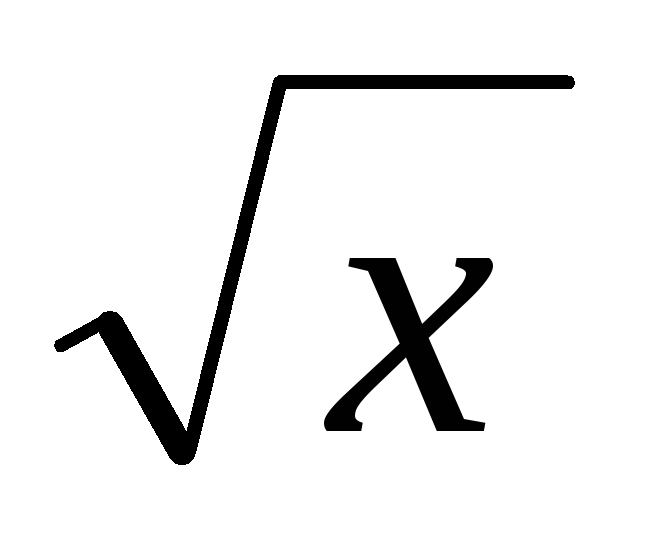 – ctg3x + sin45o
– ctg3x + sin45o -
y = sin(ctgx)
-
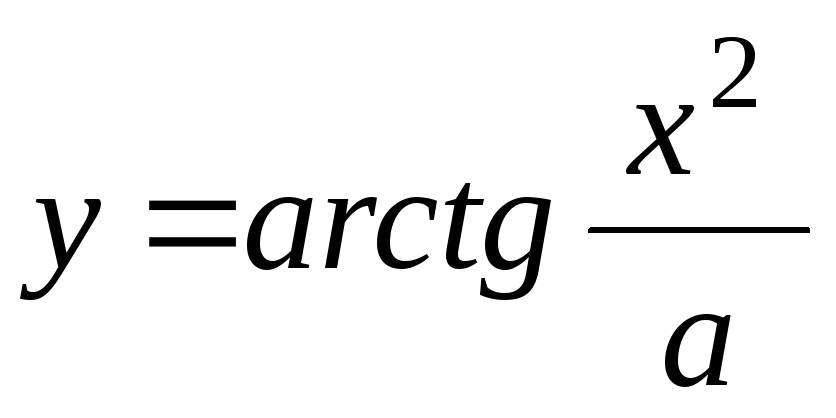
-
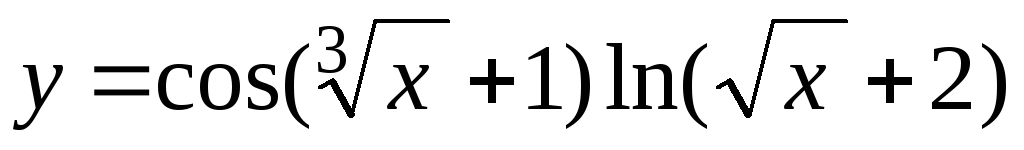
-

-
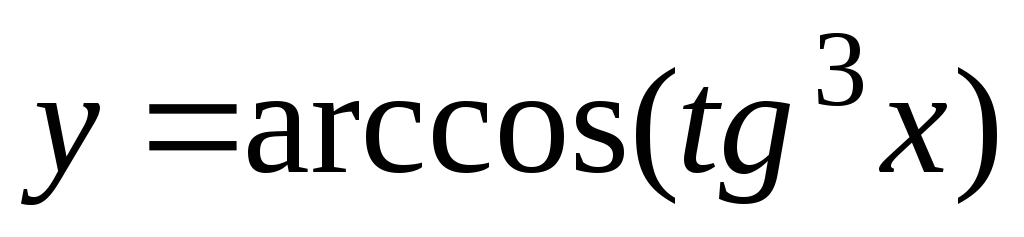 – 3ctg3
– 3ctg3 -

-
y = sinnx.cosmx + (m + 3)6
-
y = sec2x – cos2(tg3x)
-
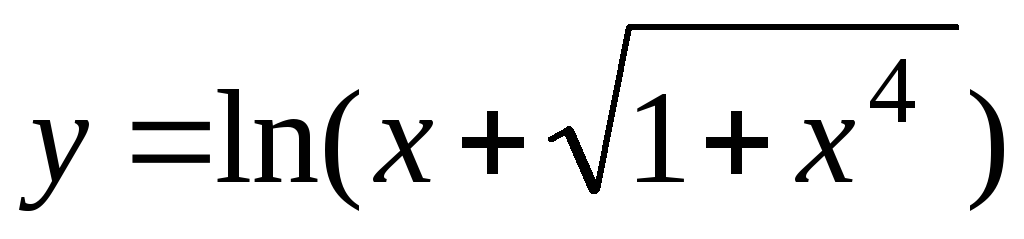
-
y = ex + eex
-

-
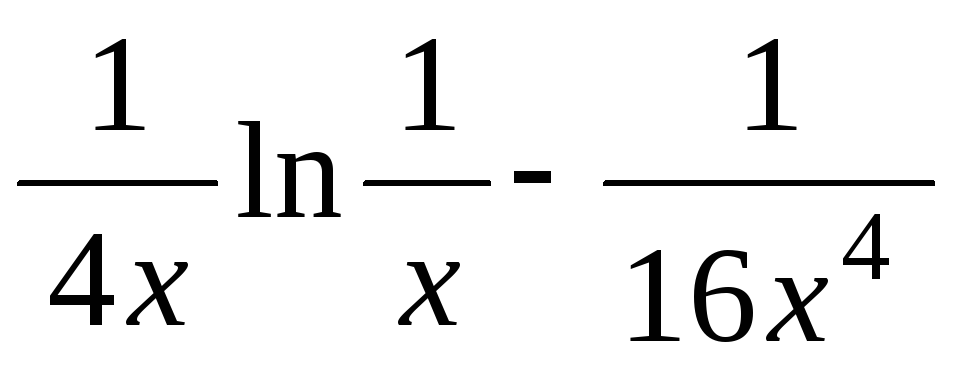
-

-
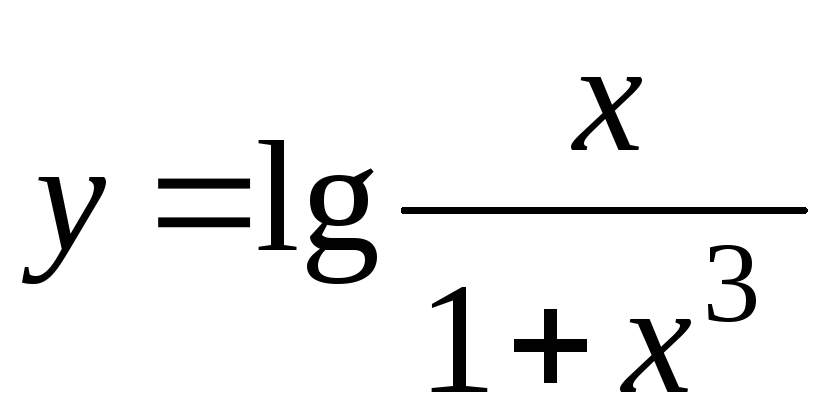 + 4ln3
+ 4ln3 -

-

-
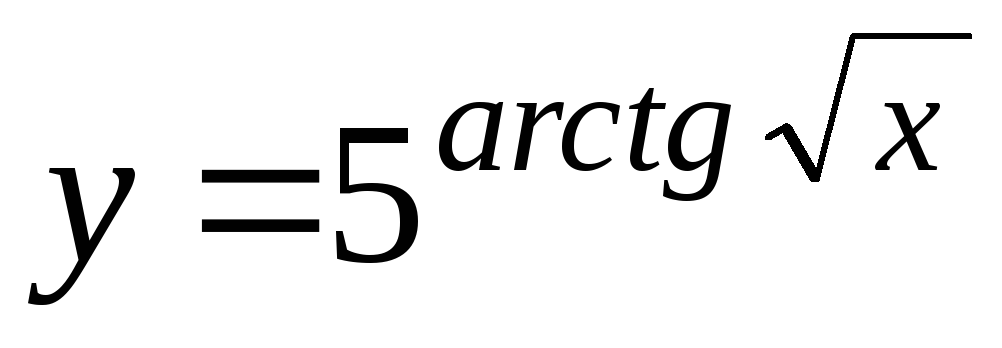 –
6tg2
–
6tg2 -
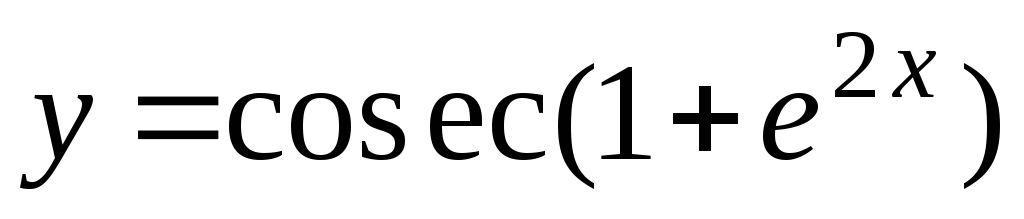
-


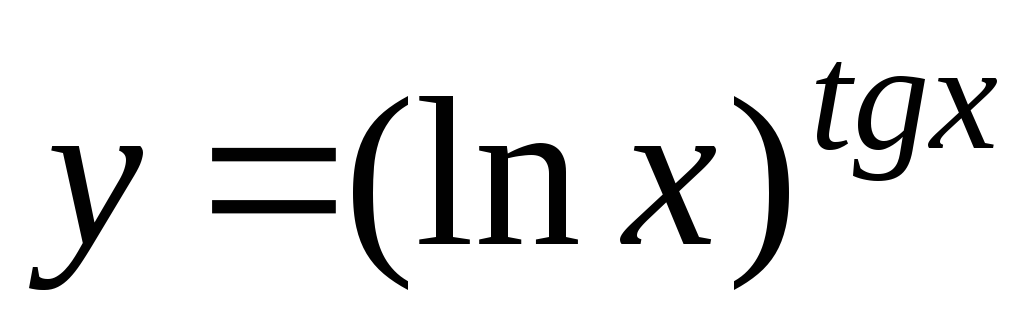
-

Найти производную функции, заданной неявно:
25. x(y2 – y) + tgy = 2x, найти у(0) 26. cos(xy) + ln(y–x) + ex = 1
Найти
![]() и
и
![]() :
:
27.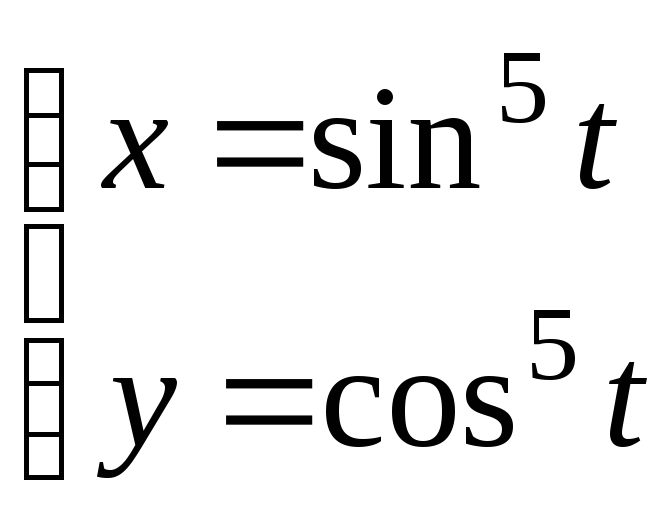 29.
29.
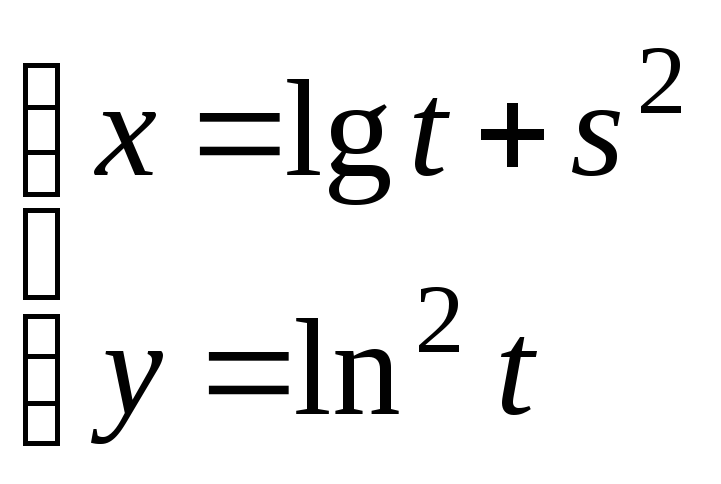
28.
 30.
30.
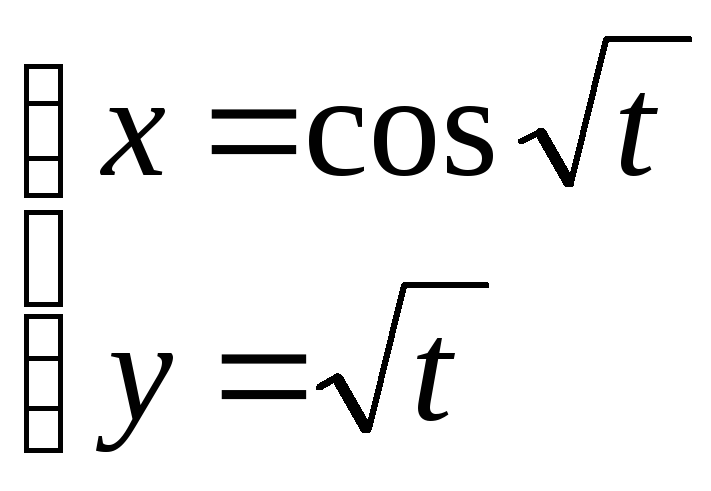
31. Найти
у(п):
![]()
Вариант 3
Найти производную первого порядка функции у(х)
-
у=5х7 – 3х4 +
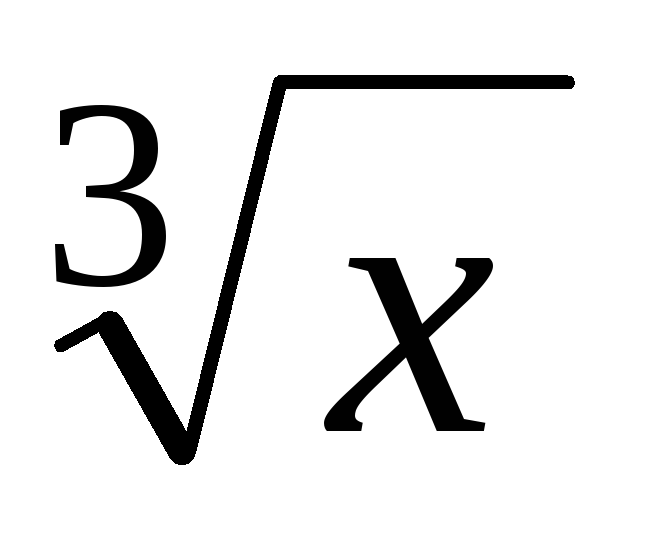 +1,
найти у(1)
+1,
найти у(1) -
, Найти у(0)
-
у = (3х + 5)(х+2)4 – cos30o
-
у = ctg
 +sinx
+ cos3x
+sinx
+ cos3x -
y = arctg
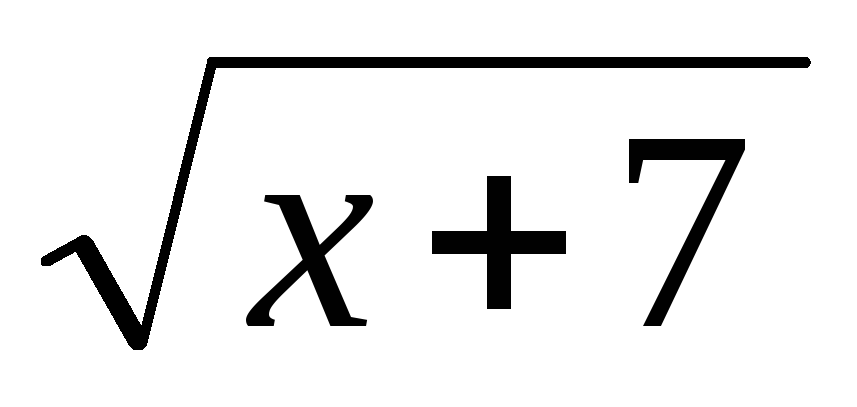 – 86
– 86 -
y = sin(ctgx)
-
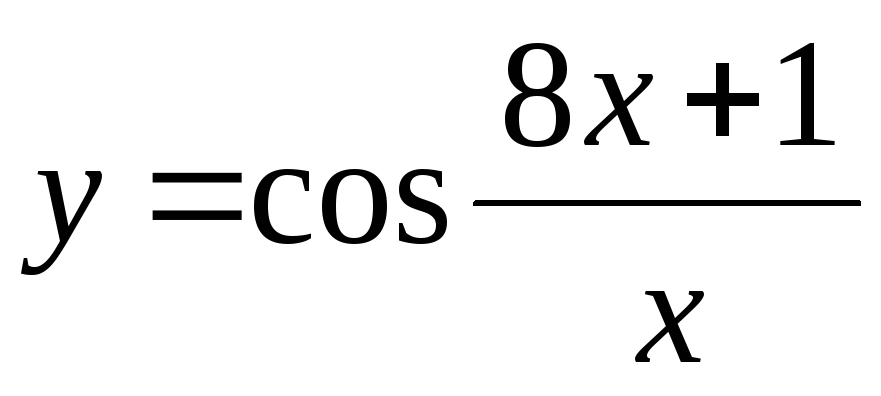 –3cos2
–3cos2 -

-
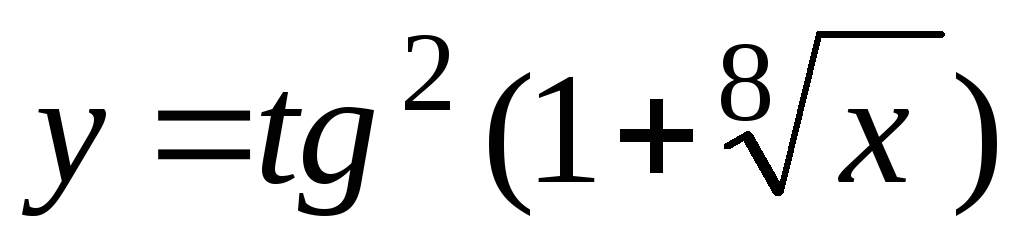
-
y = arcsin2(x +
 )
) -
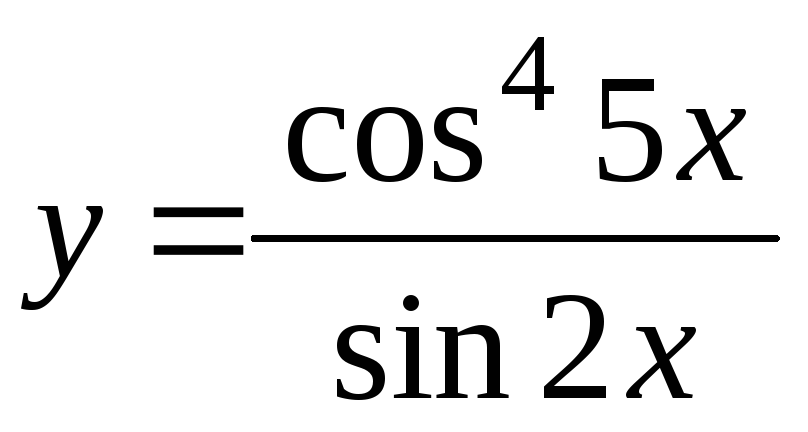
-
y= arctg(sin2x)
-
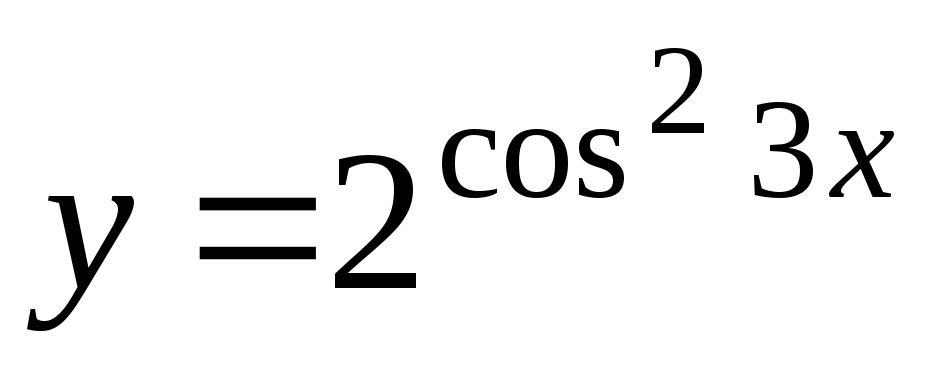 +
5tga
+
5tga -
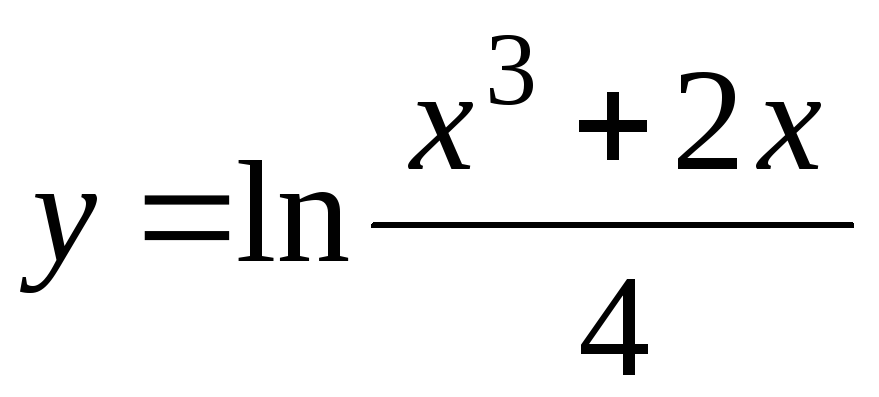
-
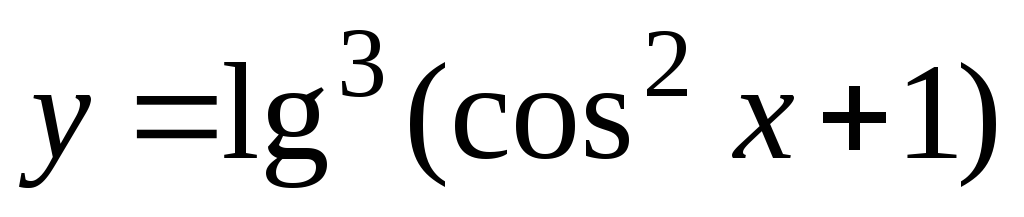
-

-
y = ln2(x –
 )
) -
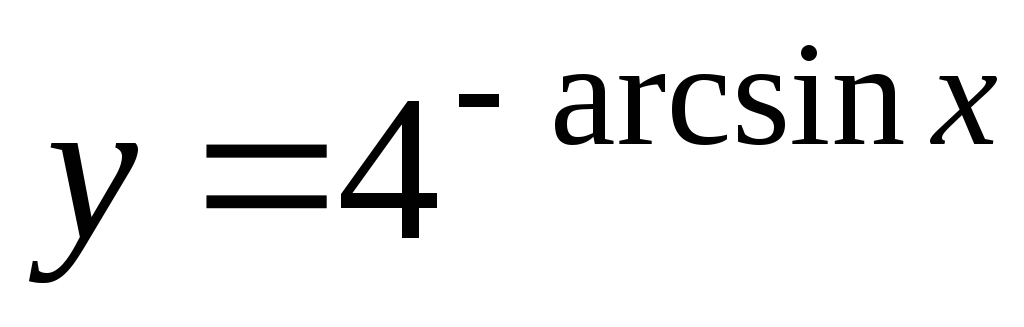
-
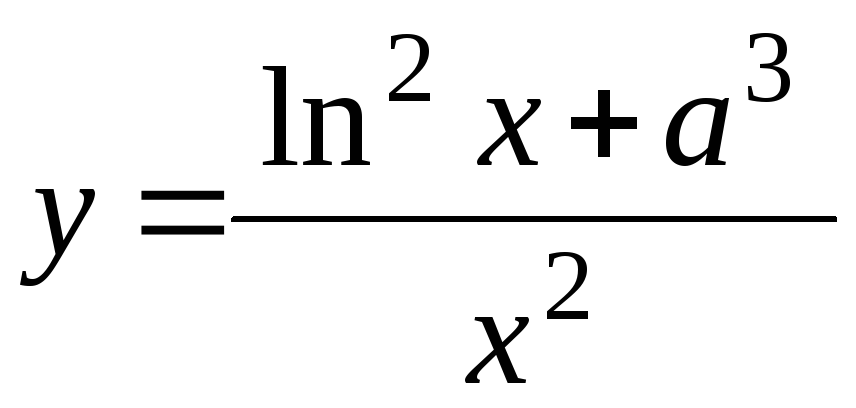
-

-
 –
e
–
e -
y = arcsin2(lgx)
23.![]()
24. y = xtgx
Найти производную функции, заданной неявно:
25.
![]() ,
найти у(0)
26. y –0,3siny
+ ex
= 1–x
,
найти у(0)
26. y –0,3siny
+ ex
= 1–x
Найти
![]() и
и
![]() :
:
27. 29.
29.
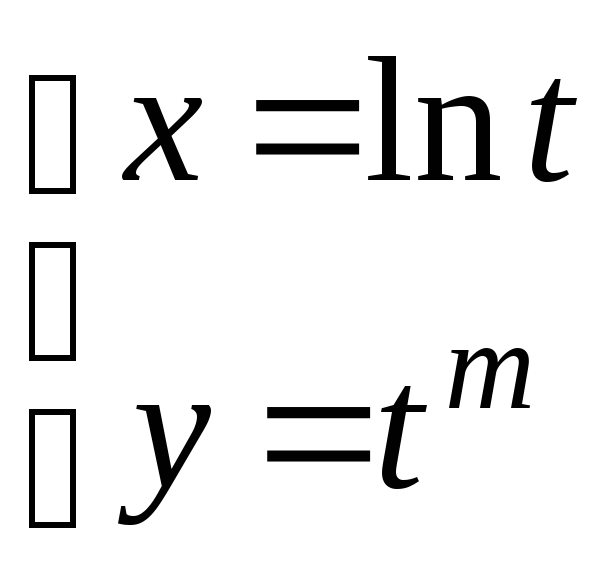
28.
 30.
30.

-
Найти у(п):
Вариант 4
Найти производную первого порядка функции у(х)
-
, Найти у(1)
-
, Найти у(0)
-
у =
 (х
– 7)2
(х
– 7)2 -
y = cos2x + 5tg(x2 – 2)
-
y = arctg(cosx) + arccose3
-
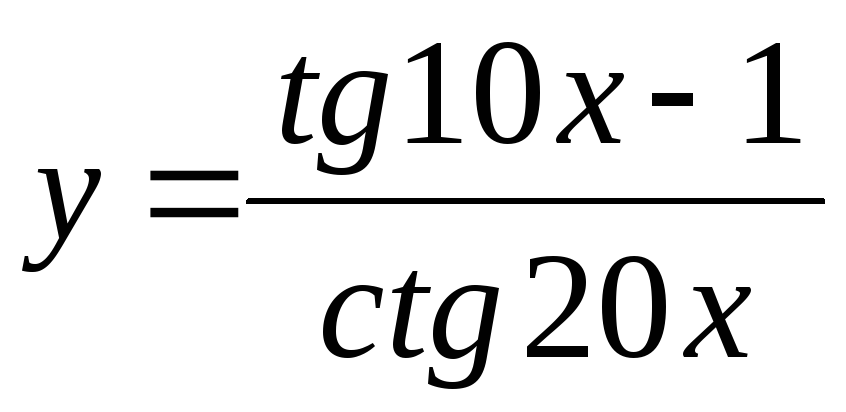
-
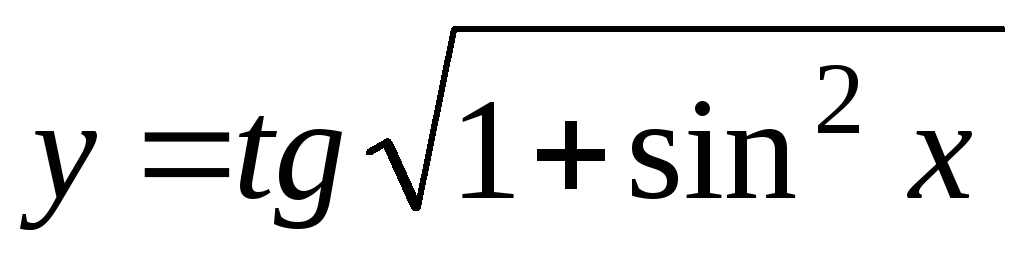 +tg20
+tg20 -
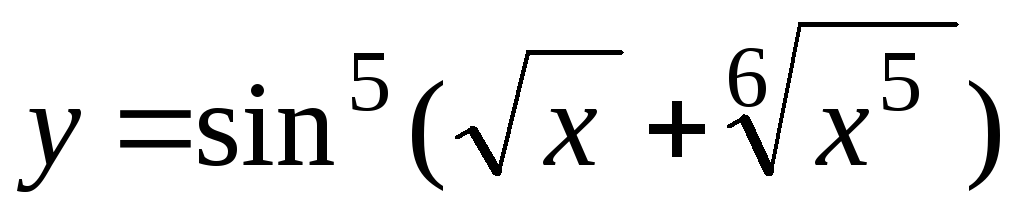
-

-

-
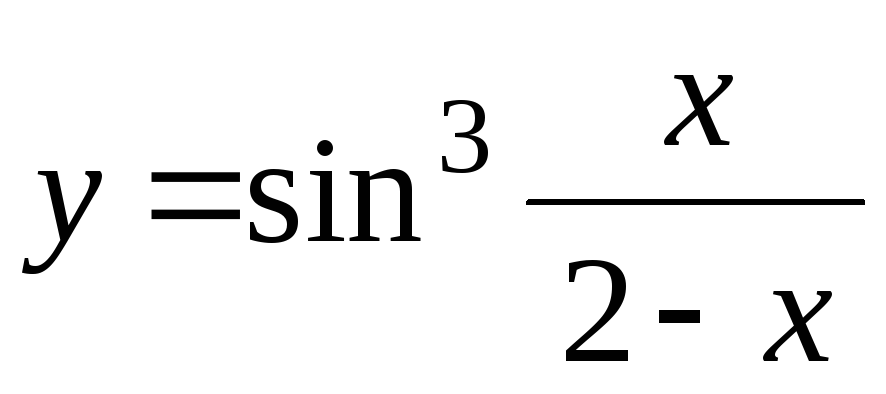
-
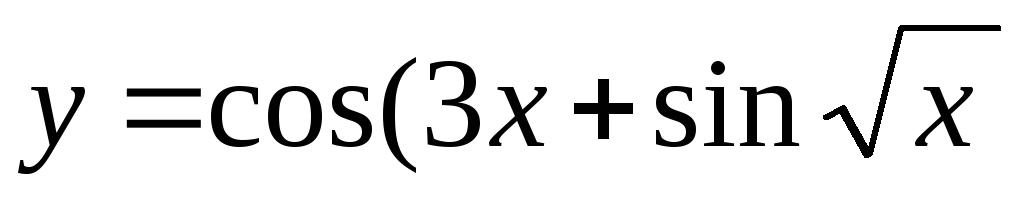 )
– sin30o
)
– sin30o -
 +
a2
+
a2 -
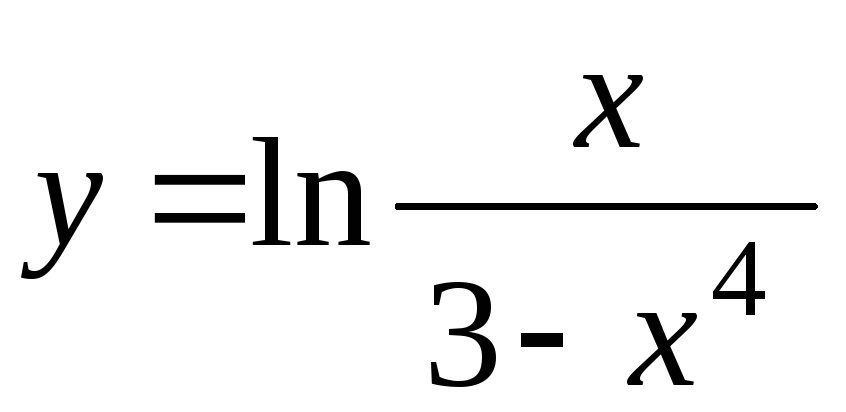
-
y = lg(x3 –7x)
-
 –4tg2
–4tg2 -
y = ln3(xcos4x)
-
y = sec(2 – e-x)
-

-

-
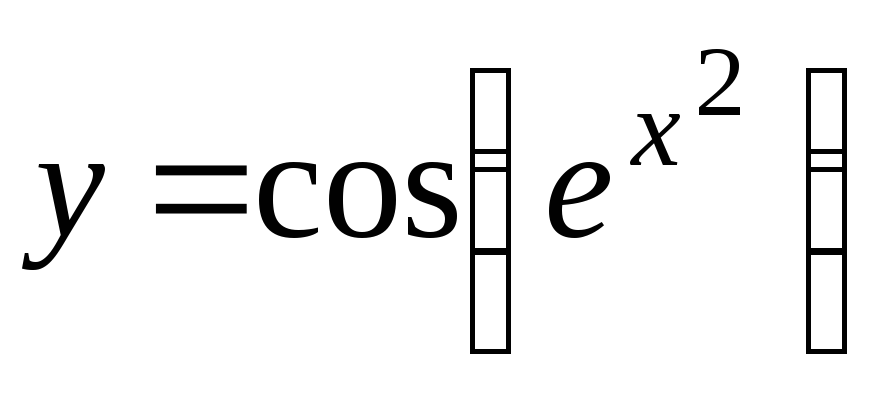
-
y = 3xln(x5 + 1)
-
y = (secx)x
24. y = (ln(x+3))tgx
Найти производную функции, заданной неявно:
25. y2 + tgxy = 9a, найти у(0) 26. cosy + exy = x
Найти
![]() и
и
![]() :
:
27. 29.
29.

28.
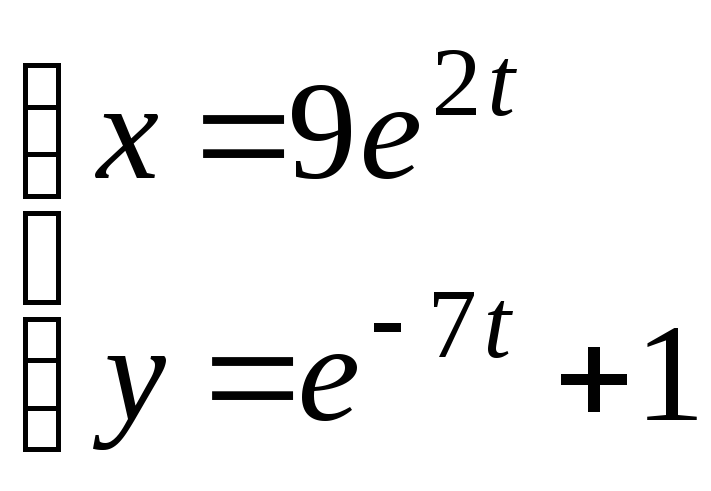 30.
30.
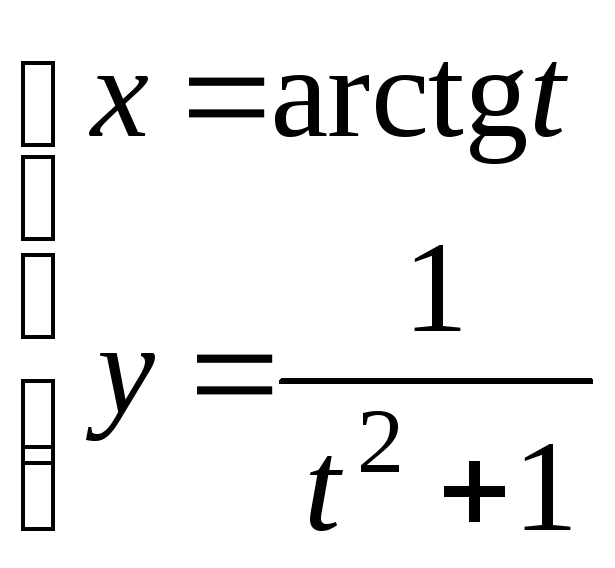
31. Найти у(п):
Вариант 5
Найти производную первого порядка функции у(х)
-
у = х7 –2х2 +
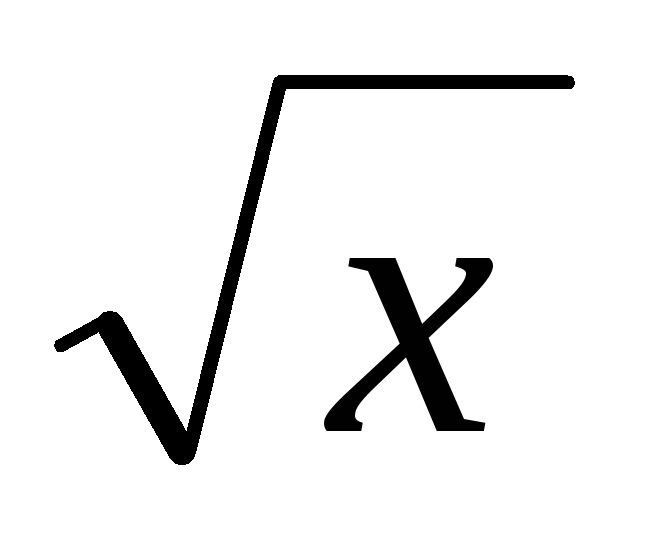 +4,
найти у(1)
+4,
найти у(1) -
, Найти у(1)
-
у = (4х + 5)2(2х –4) –sin3
-
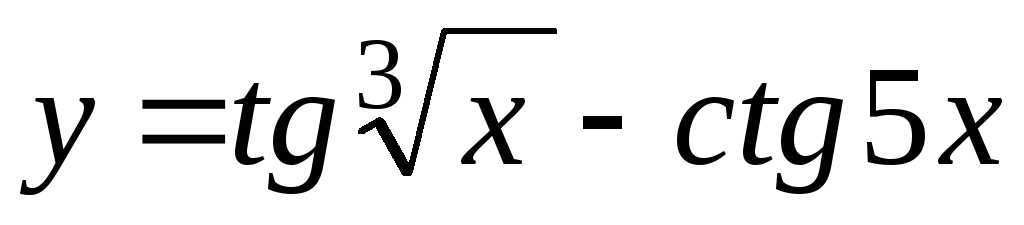
-
у = arcsin(lnx)
-

-

-
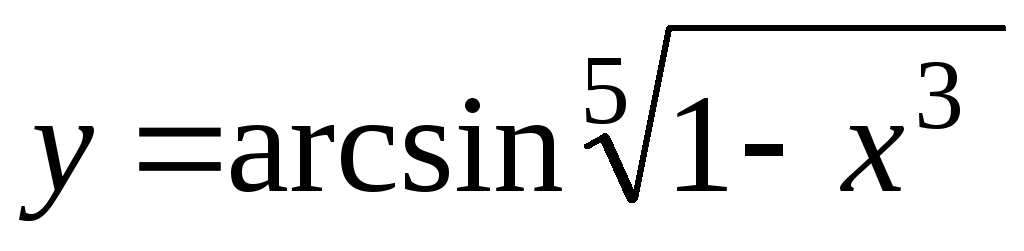
-
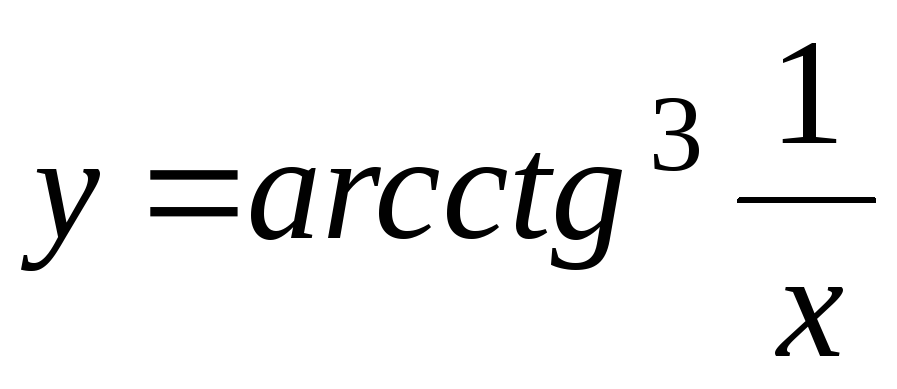
-
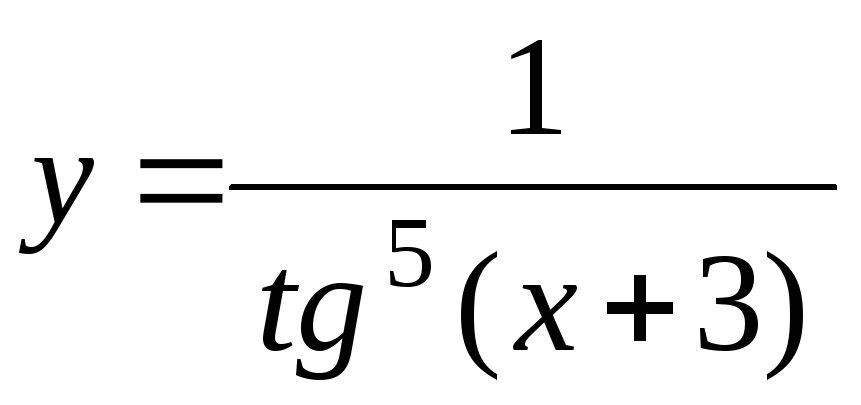 +
tg 7
+
tg 7 -

-
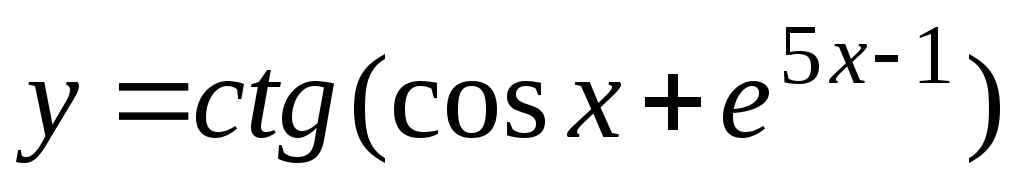
-
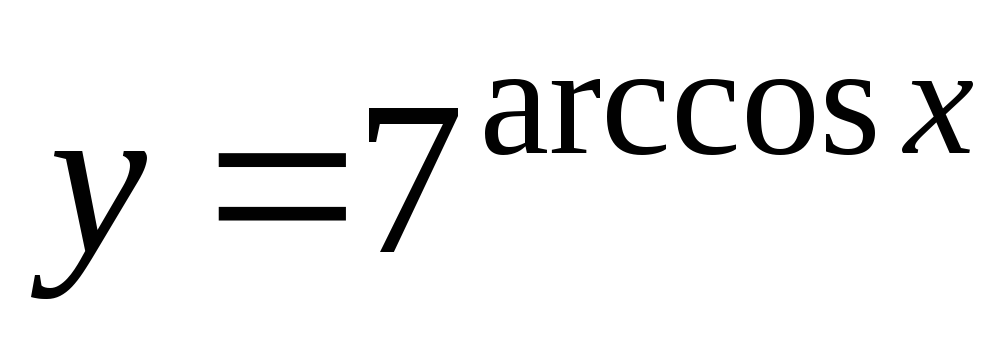
-

-

-
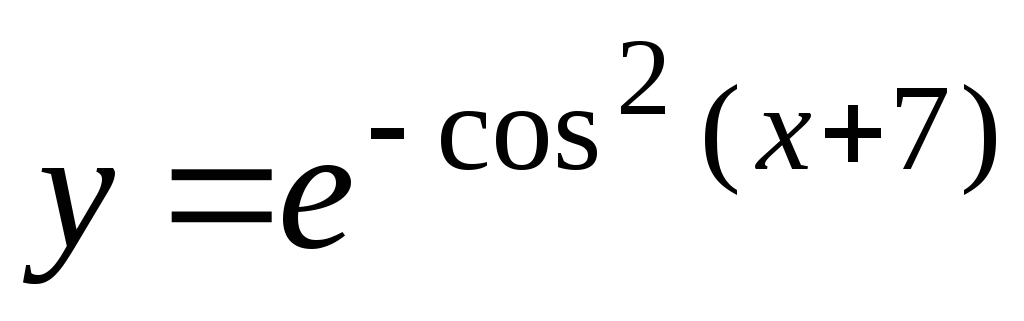 +lg4
+lg4 -

-
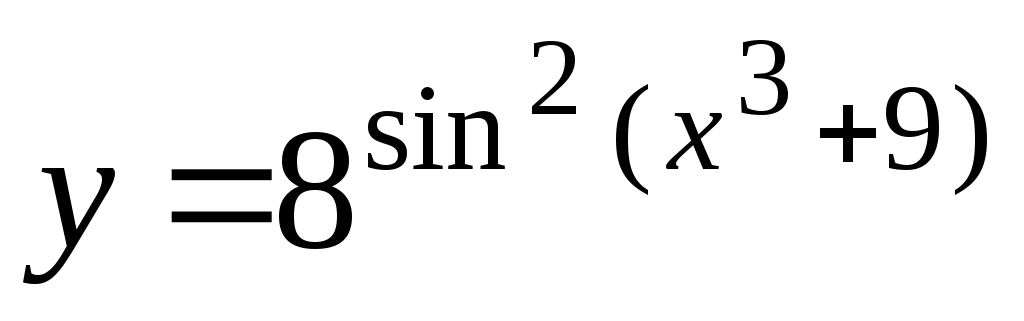
-

-
y = lg(arctgx)
-
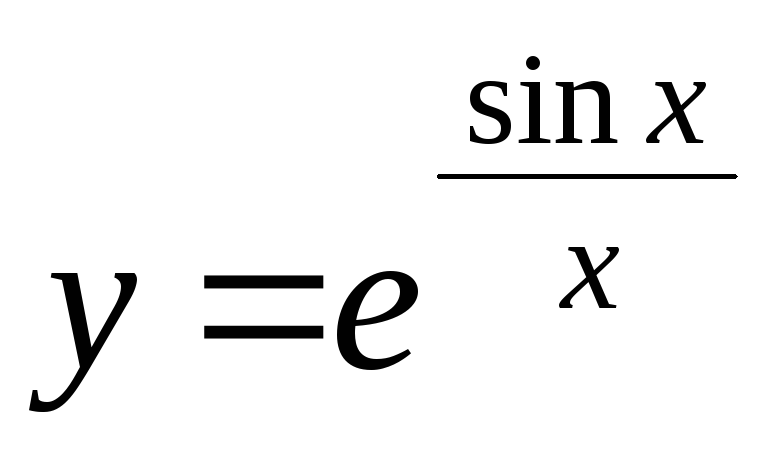
-
y = ln(1+arctg2x)
-
y = 6 +(arcsinx)3x
-
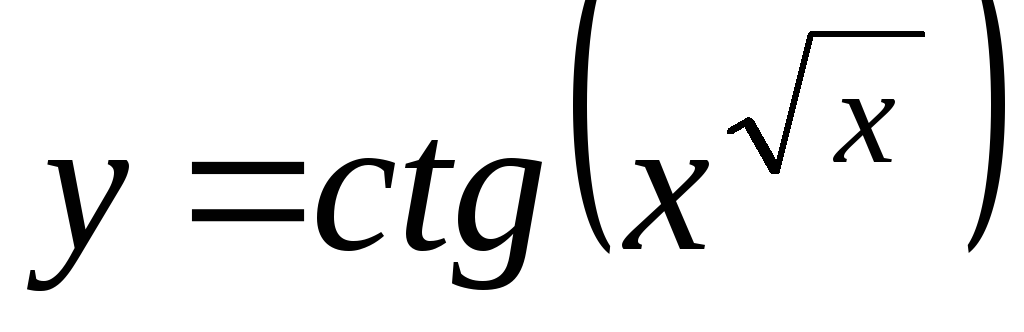
Найти производную функции, заданной неявно:
25. yx
= xy, найти
у(2)
26.
![]()
Найти
![]() и
и
![]() :
:
27.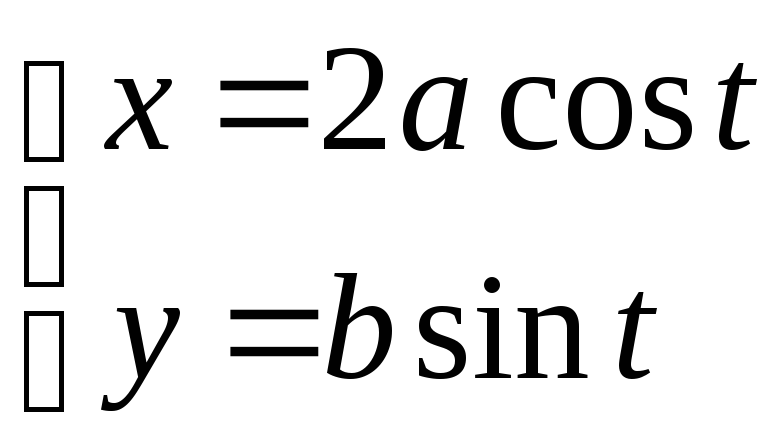 29.
29.
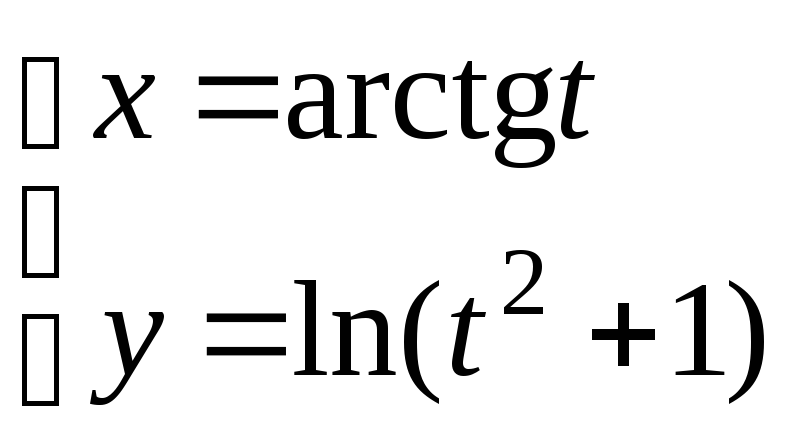
28.
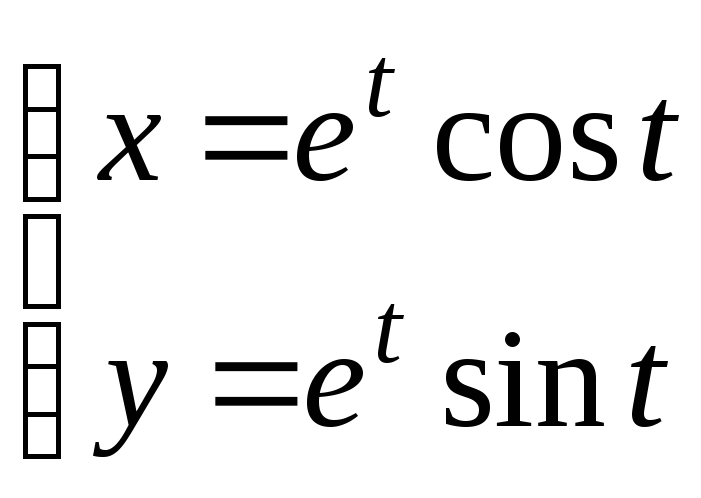 30.
30.

31. Найти у(п):
Вариант 6
Найти производную первого порядка функции у(х)
-
y= 5х9 – 7х2 +
 – 6 , найти у(1)
– 6 , найти у(1) -
, Найти у(–1)
-
у = (5х + 8)3(2х – 3)4
-
у = ctg
 – tg8x
– tg8x -
y = arcsin(tgx)
-
y= sin(x +
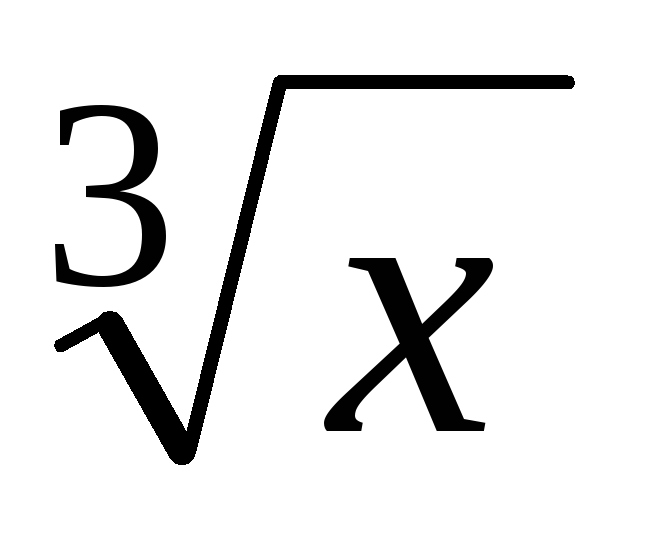 )
) -
y = cos(6–
 ).tg(7
).tg(7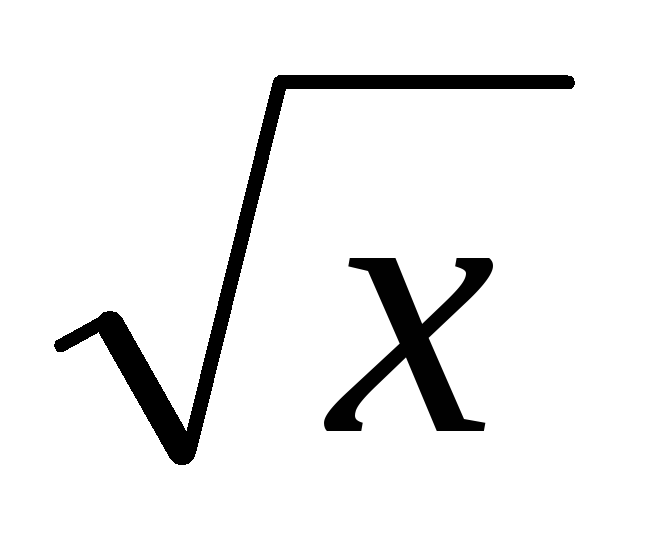 )
) -
 – a4
– a4 -
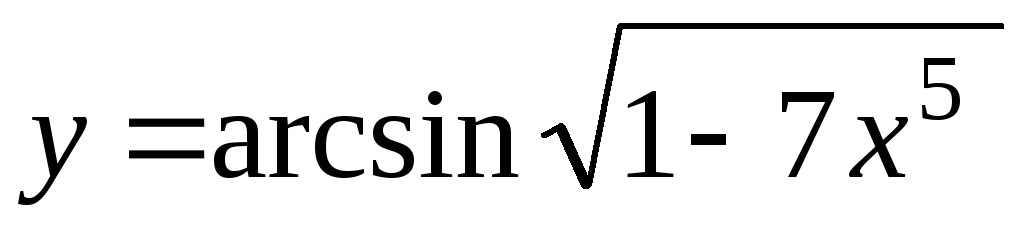
-
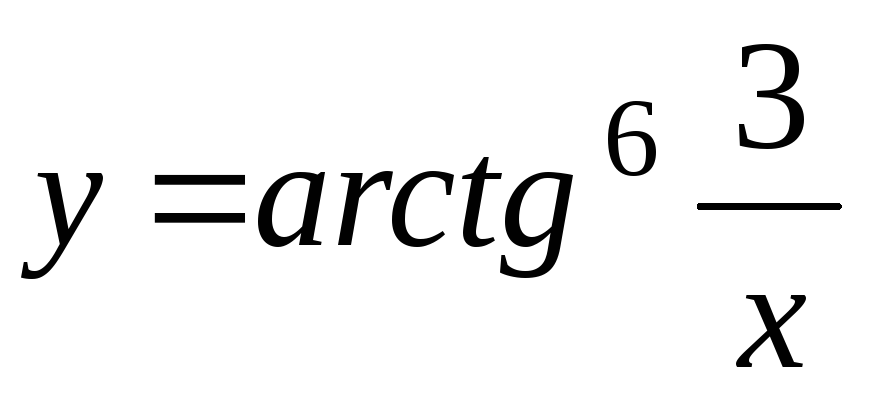
-
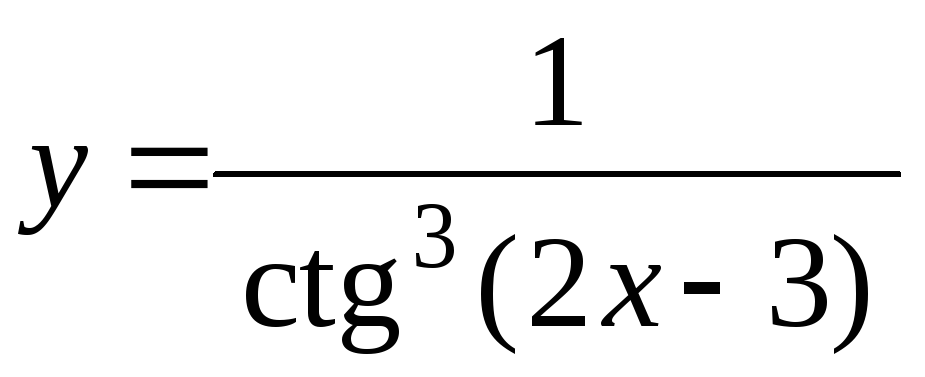
-
y = ctg(3cosx +
 )
) -
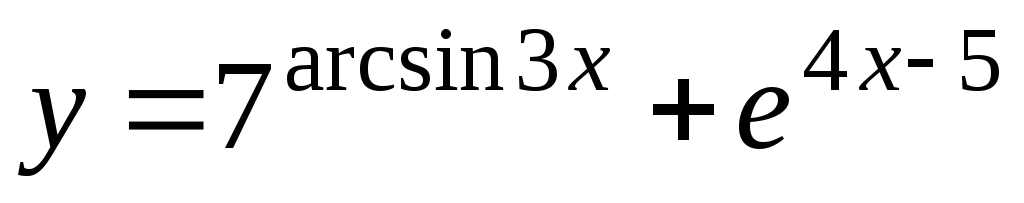
-
 +e5
+e5 -
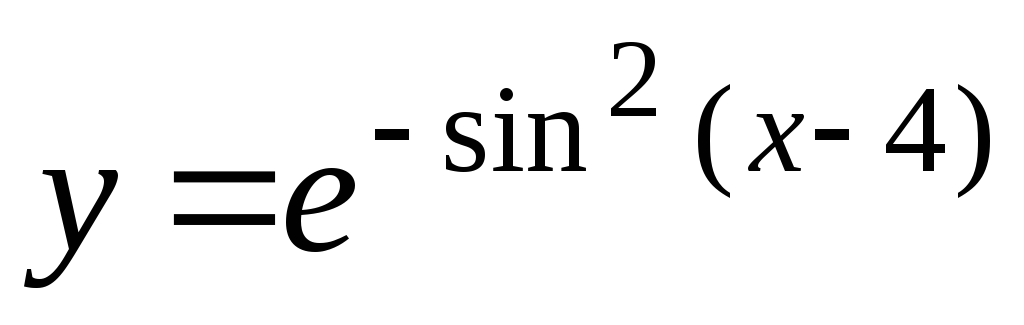
-
y = lg4(
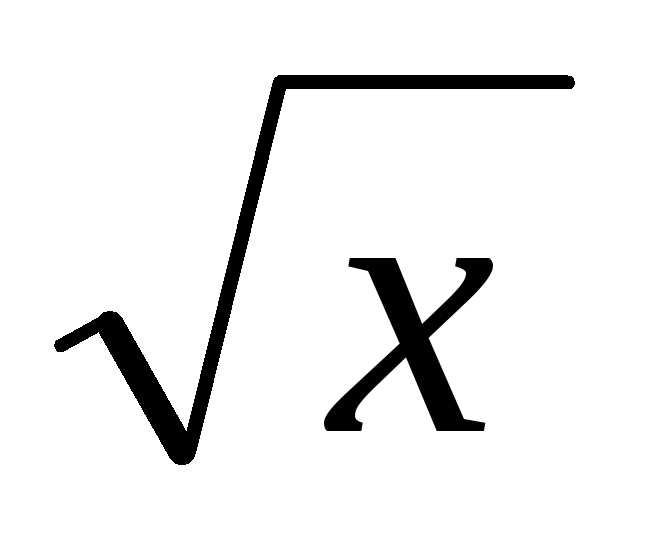 –5)
–5) -
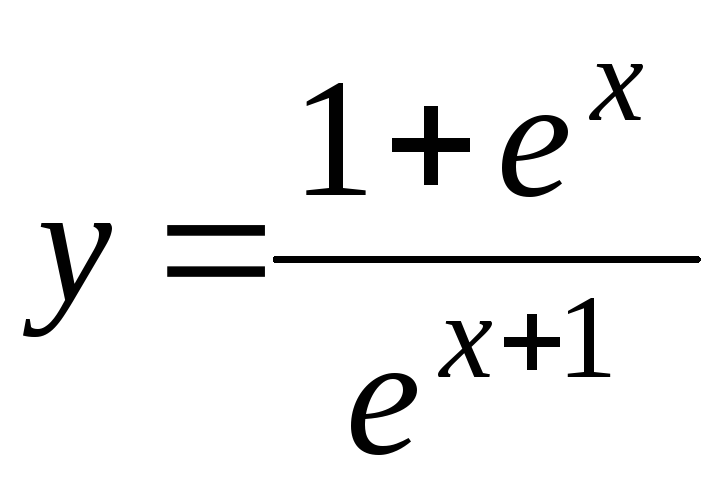
-

-

-
y = lg(arctg4x) + lg6
-

-

-
y = (3arcsin2x)4x
-

Найти производную функции, заданной неявно:
25. y
– x
= eyarctgx,
найти у¢(0)
26.
![]()
Найти
![]() и
и
![]() :
:
27.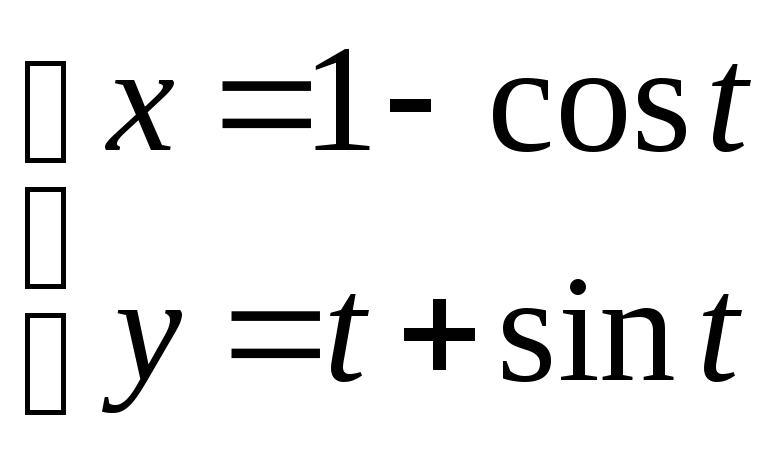 29.
29.
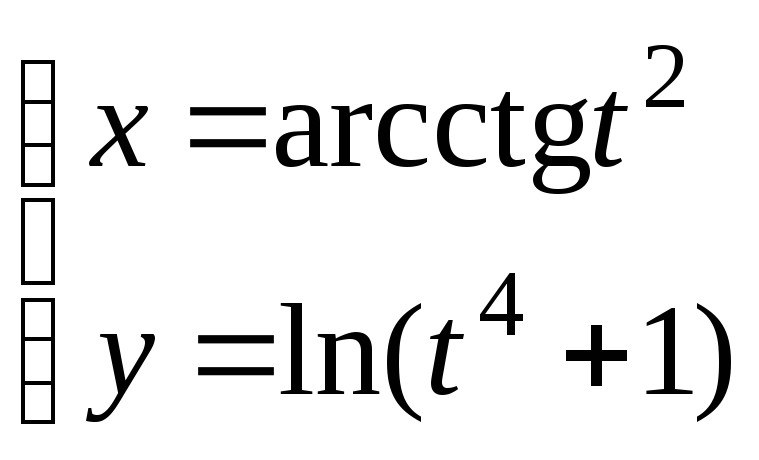
28.
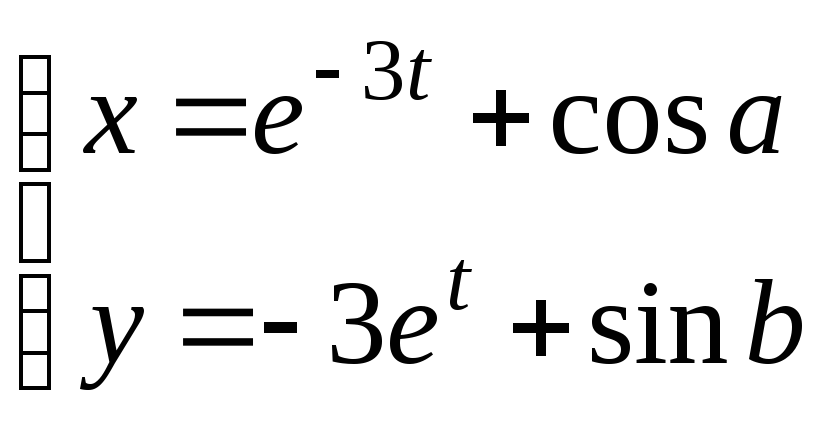 30.
30.
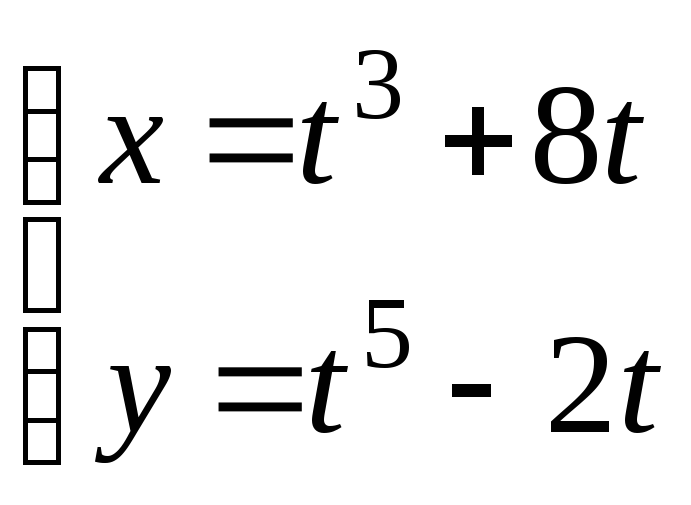
31. Найти у(п):
Вариант 7
Найти производную первого порядка функции у(х):
-
y = 7x3 – 8x + 2
 –3,
найти у(1)
–3,
найти у(1) -
y =
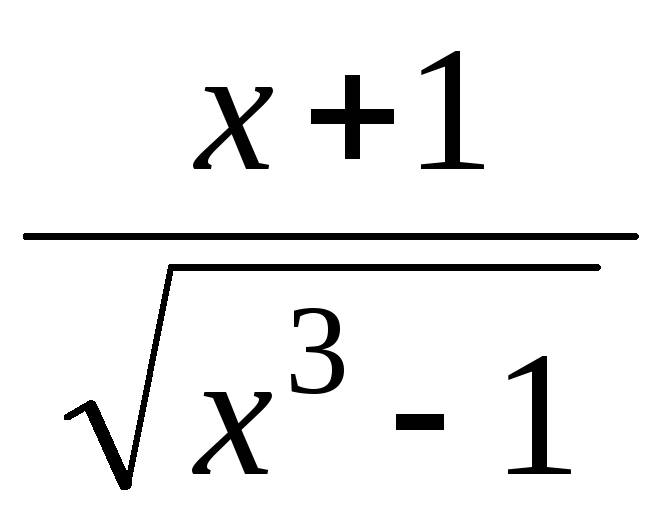 ,
найти у(2)
,
найти у(2) -
y=

-
y=arcsin
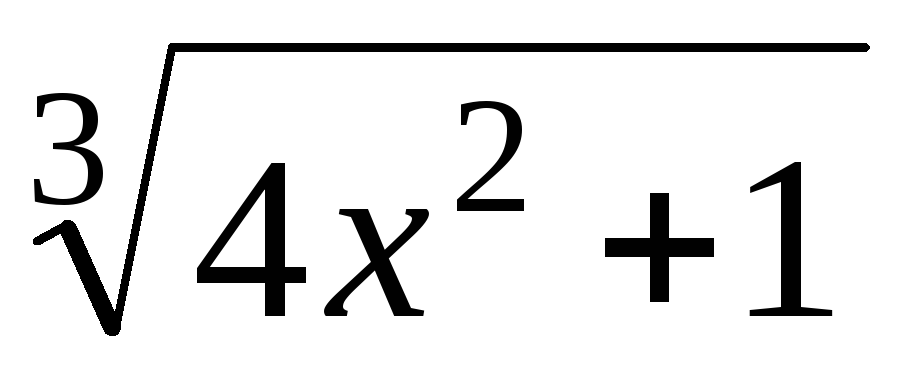 +
sin
+
sin -
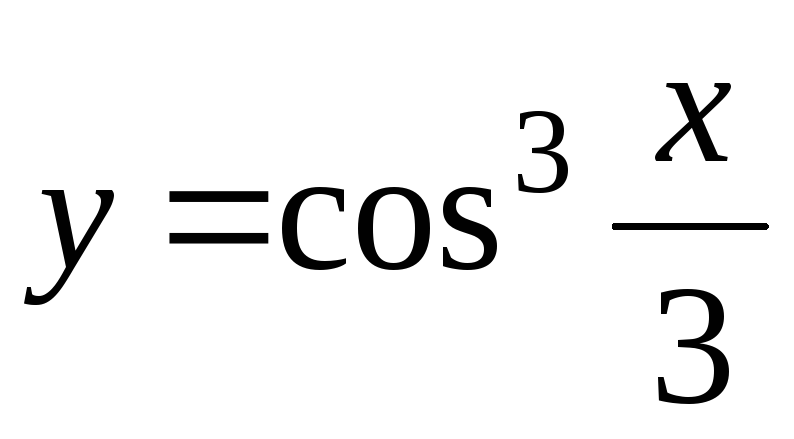
-
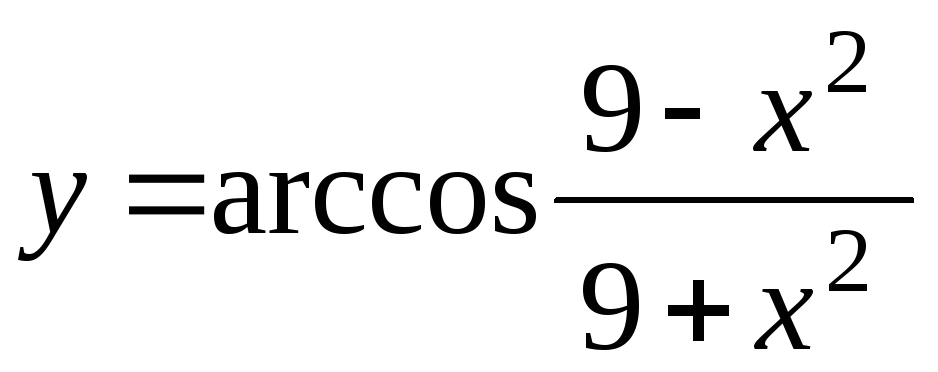
-

-

-

-
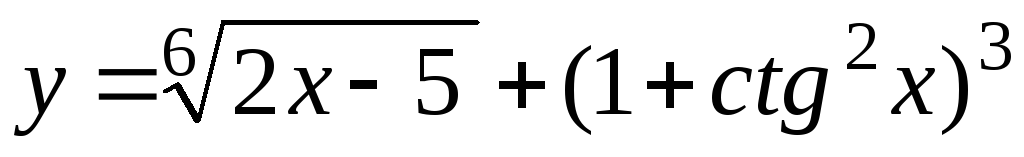
-
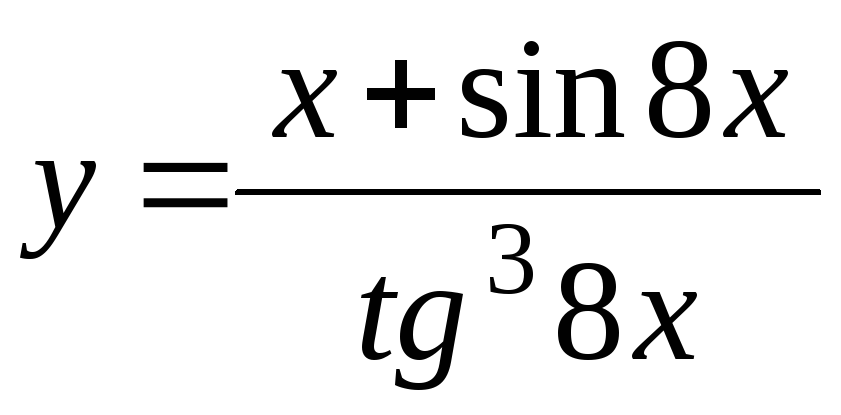
-

-
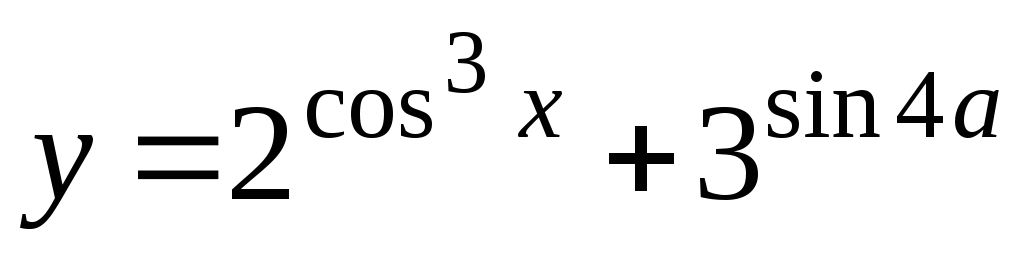
-
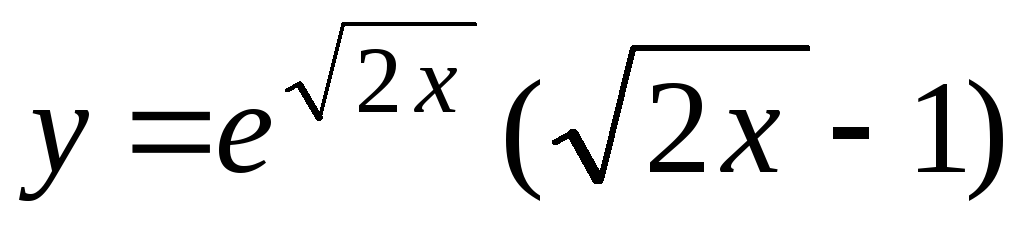
-
y = 6–x – sine–x .cose–x
-

-

-

-
y = lg(1+cos2x)
-
y= log2(sin2x+ tg3x)
-
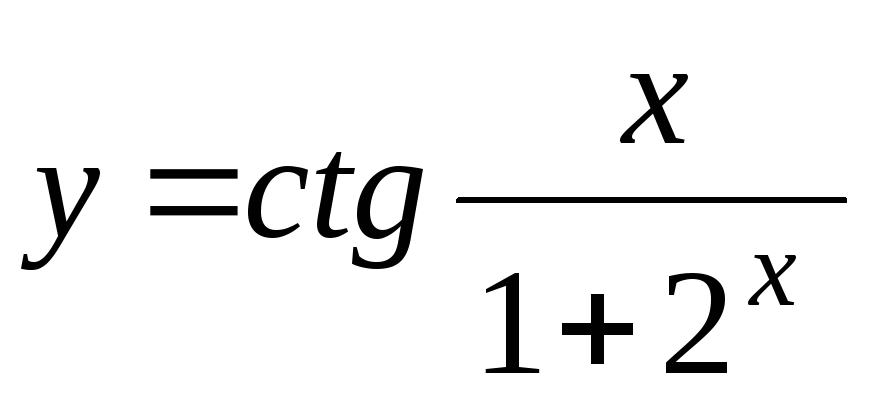
-
y = arcctg( 1+ 5ln3x)
-

24. y = xlnx
Найти производную функции, заданной неявно:
25. y2
= x3
+ 4y – 3
, найти у¢(0)
26.
![]()
Найти
![]() и
и
![]() :
:
27. 29.
29.
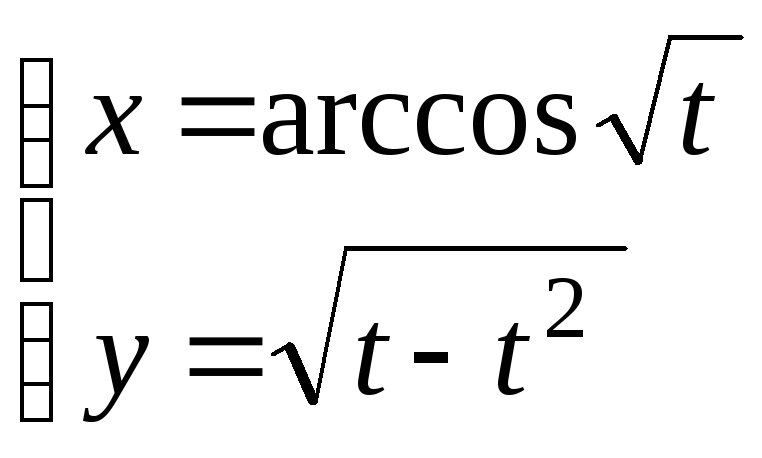
28.
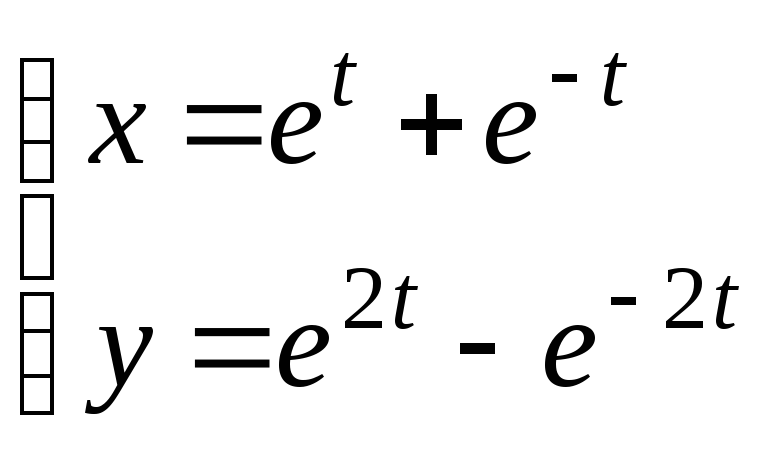 30.
30.