
Вопросы к защите темы «Функции нескольких переменных»
Понятие функции нескольких переменных, ее область определения. Привести примеры функции 2-х, 3-х, п переменных. Что представляет собой область определения функции двух переменных?
Каково геометрическое изображение функции 2-х переменных?
Дайте определение линии, поверхности уровня, приведите примеры.
Предел ФНП, непрерывность ФНП.
Определение частного приращения ФНП, частных производных 1-го, 2-го, 3-го и т.д. порядков. Запишите определение частных производных первого порядка для функции
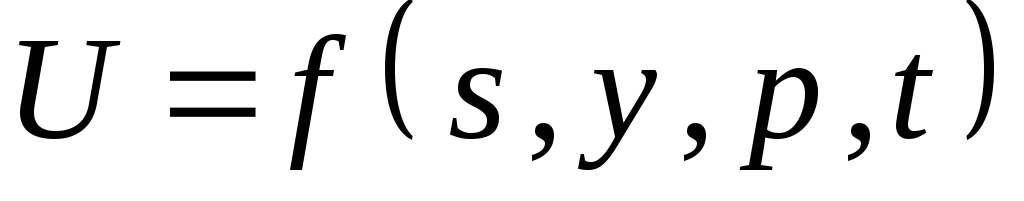 .
.Физический смысл частных производных 1-го порядка.
Понятие дифференцируемости ФНП, полного дифференциала, связь между этими понятиями. Частные дифференциалы, формула полного дифференциала 1-го ,2-го порядков. Запишите формулу нахождения
 функции
функции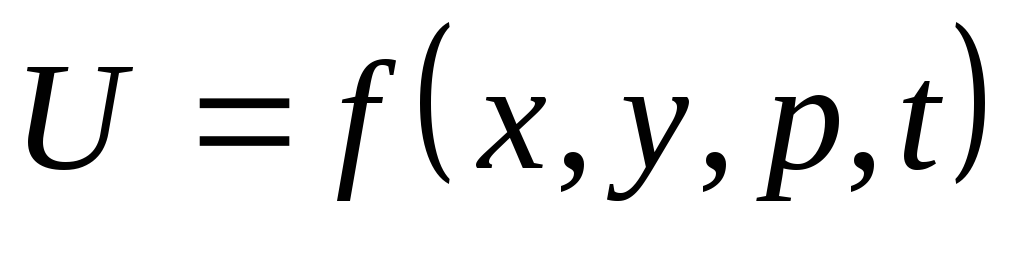 .
.Производная по направлению, градиент, их свойства и связь (с доказательством), физический смысл. Заполните пропуски в следующей фразе «Производная функции U = f(x,y,z) по направлению вектора s характеризует . . . . . . функции в . . . . . . . Это производная вычисляется по формуле
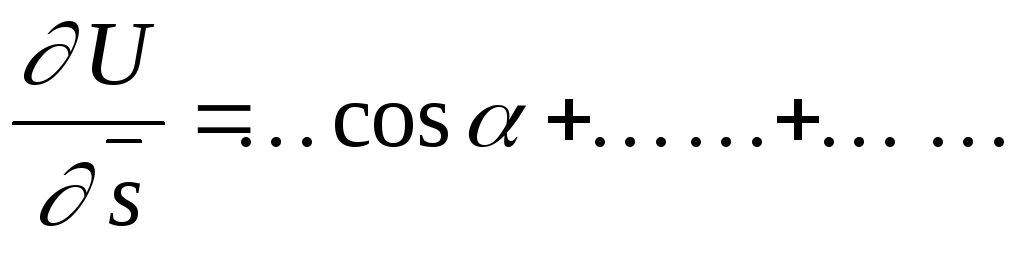 ,
где
,
где »
.
»
.Установите соответствие между символами 1- 4 и тем, что характеризуют (а – г) математические объекты, обозначенные этими символами: 1. dz , 2. grad z, 3.
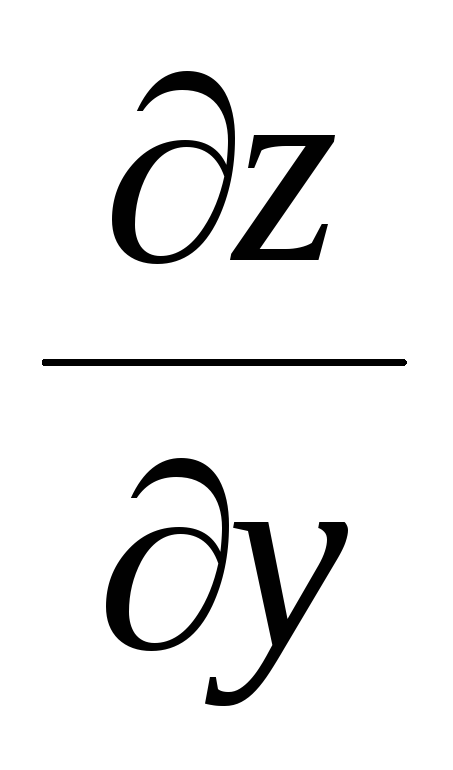 ,
4.
,
4. ;
а) скорость изменения функции z
= f(x,
y)
в направлении
оси ОУ; б) приращение функции при малых
приращениях аргументов; в) скорость
изменения функции в направлении
вектора; г) направление наискорейшего
возрастания функции.
;
а) скорость изменения функции z
= f(x,
y)
в направлении
оси ОУ; б) приращение функции при малых
приращениях аргументов; в) скорость
изменения функции в направлении
вектора; г) направление наискорейшего
возрастания функции.Линеаризация функции одной и нескольких переменных, ее геометрическая интерпретация, формула линеаризации. Касательная плоскость.
Неявная функция 1-й, 2-х, 3-х и т.д. переменных. Дифференцирование неявных функций (запишите формулы нахождения частных производных). Привести примеры для функций 1-й, 2-х, 3-х переменных.
Определение точек максимума и минимума ФНП, экстремумов ФНП.
Необходимое условие существования экстремума (с доказательством), критические точки, их связь с точками экстремума.
Достаточное условие существования экстремума ФНП, частный случай функции 2-х переменных.
Сформулируйте алгоритм нахождения экстремума функции z = f(x,y).
Условный экстремум, его геометрический смысл, способы его нахождения.
Наибольшее и наименьшее значения ФНП в замкнутой ограниченной области, условия их существования для ФНП, графический и аналитический методы их нахождения.
Метод наименьших квадратов, его суть Какая задача решается методом наименьших квадратов? Опишите принцип решения этой задачи.
Если по характеру расположения точек (хк , ук) на координатной плоскости выбран вид аналитической зависимости у = ах +b(илиу = ах2 + bх + с, или у = ах + b). Изложите метод нахождения параметров а, b (с) этой зависимости.
Задачи
Для функции z = x2 + y2 –6x +4y + 25 запишите уравнение линии уровня, проходящей через точку Р(1, –4). Постройте ее.
Постройте линию уровня функции z = x – 4y + y2 , в каждой точке которой функция принимает значение 5.
Температура стержня ОХ является функцией абсциссы х этой точки и времени t: = f(x, t). Каков физический смысл частных производных
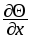 и
и ?
?Записать площадь S прямоугольника как функцию его основания b и высоты h. Найти
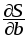 и
и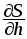 ,
указать их смысл.
,
указать их смысл. Температура Т точки остывающего стержня является функцией двух переменных: расстояния x точки от начала стержня и момента времени t:
 .
Вычислите и укажите физический смысл
.
Вычислите и укажите физический смысл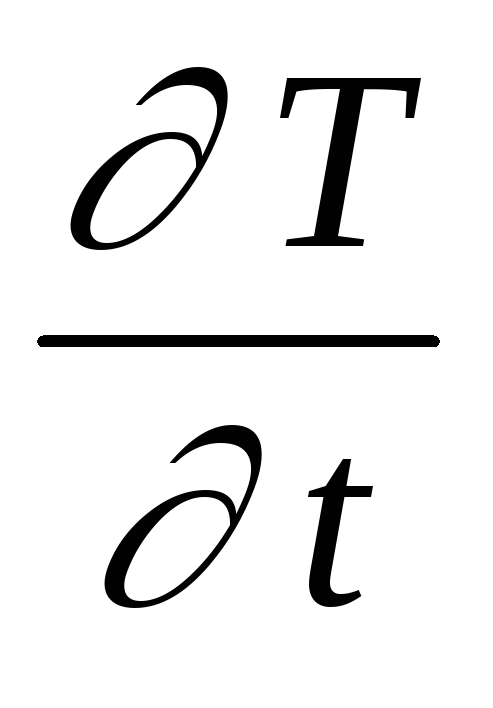 в точке Р(1,2) .
в точке Р(1,2) .
Найдите смешанные производные второго порядка функции
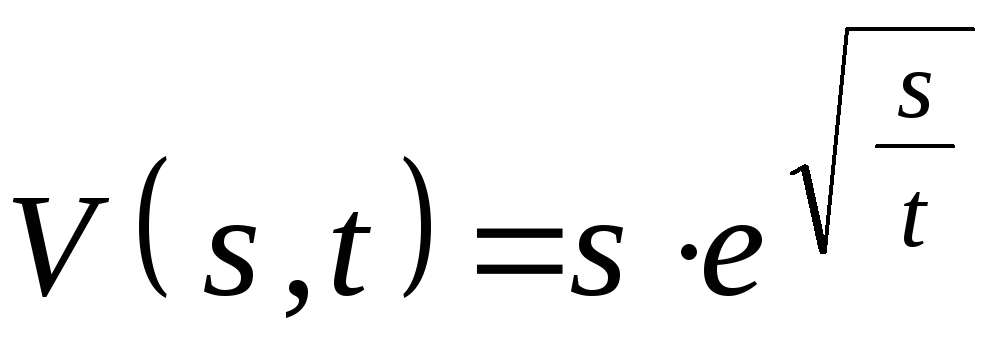 .
.Функции и(х, у, z) =
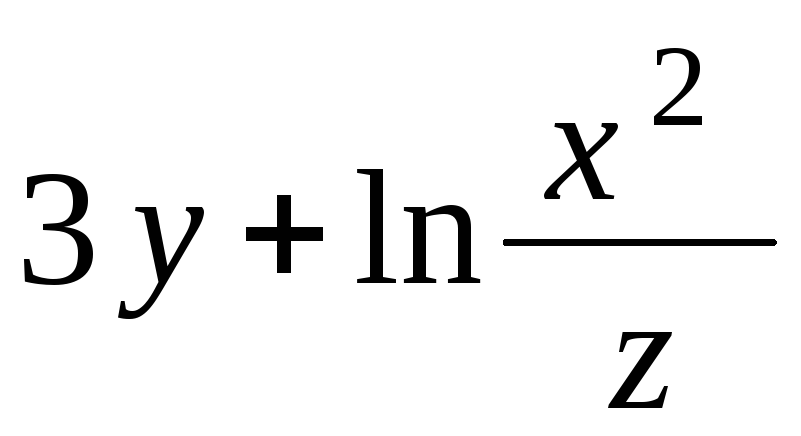 и 3х4
– 4у3z
+ 4z2xy
– 4z3x
+ 1 =0 в окрестности точки (1, 1, 1) заменить
приближенно равными им линейными
функциями.
и 3х4
– 4у3z
+ 4z2xy
– 4z3x
+ 1 =0 в окрестности точки (1, 1, 1) заменить
приближенно равными им линейными
функциями.Укажите, в каком направлении следует двигаться от точки
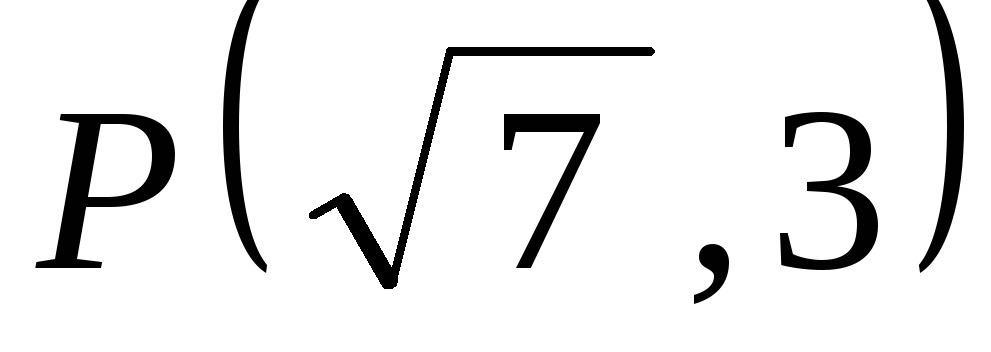 ,
чтобы функция
,
чтобы функция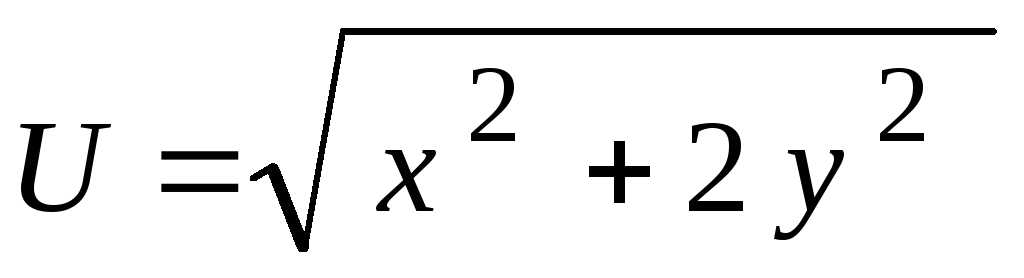 возрастала быстрее всего. Постройте
этот вектор.
возрастала быстрее всего. Постройте
этот вектор.В каком направлении должна двигаться точка М(х, у, z) при переходе через точку М0(2, 0, 1), чтобы функция
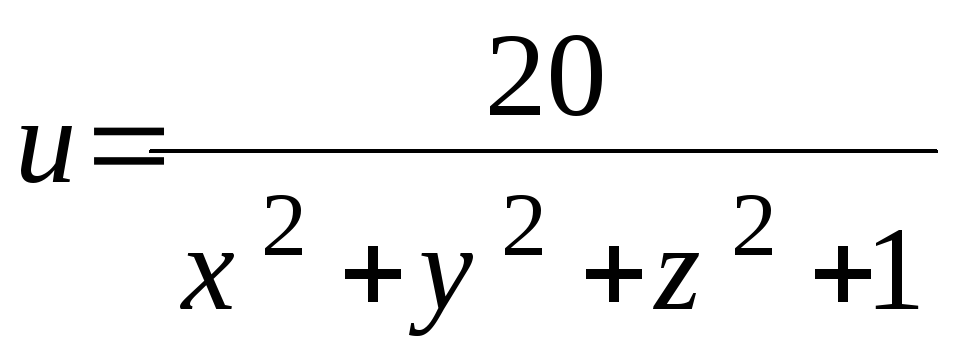 убывала с наибольшей скоростью?
убывала с наибольшей скоростью?Найти производную функции и = х2 –3хуz + 5 в точке М(1, 2, –1) в направлении, составляющем равные углы со всеми осями координат.
Скорость распределения материи в пространстве переменных r, s, t задается формулой
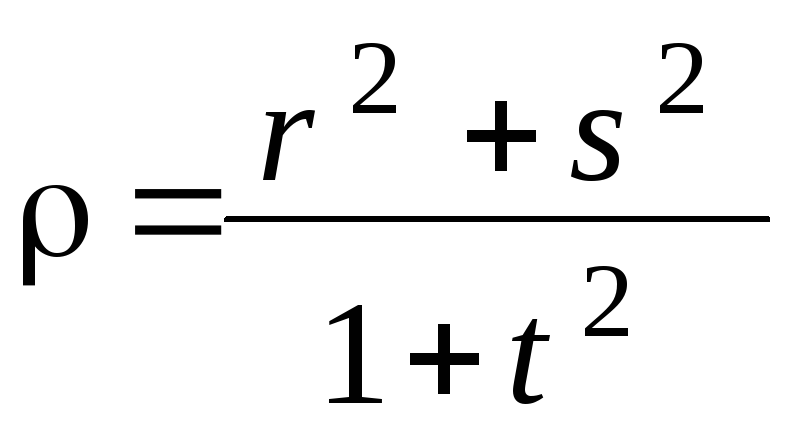 .
В каком направлении плотность в точке
М(–1, 3, 2) меняется быстрее всего? Чему
равна наибольшая скорость изменения
плотности?
.
В каком направлении плотность в точке
М(–1, 3, 2) меняется быстрее всего? Чему
равна наибольшая скорость изменения
плотности?Как изменилась диагональ прямоугольника, если одна его сторона а = 20см уменьшилась на 2% своей длины , а вторая сторона b = 30см увеличилась на 3% . (не пользуясь МК)
Заполните пропуски в таблице, если
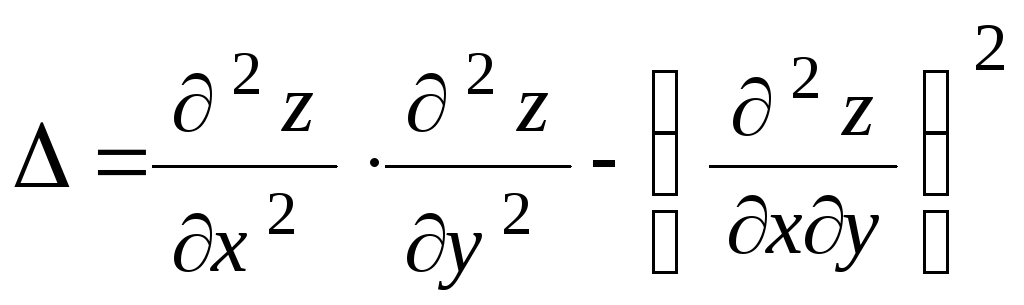 ,r
=
,r
=
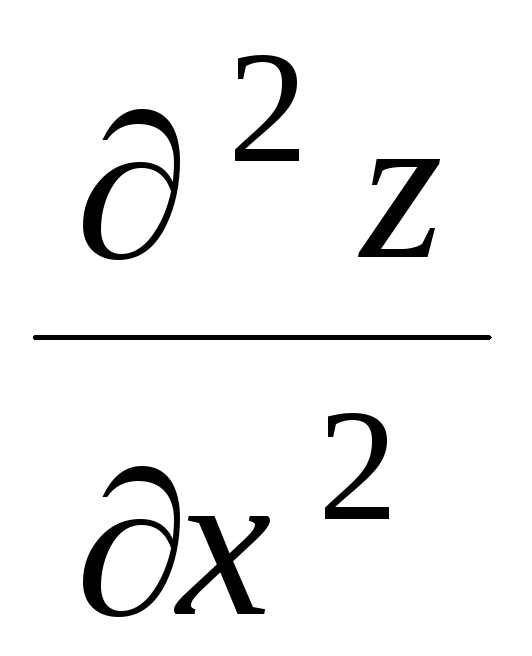 :
:Условия на
Наличие и вид
Экстремума
r
…
…
точка экстремума
…
любой знак
нет экстремума
> 0
…
точка минимума
Найдите экстремум функции

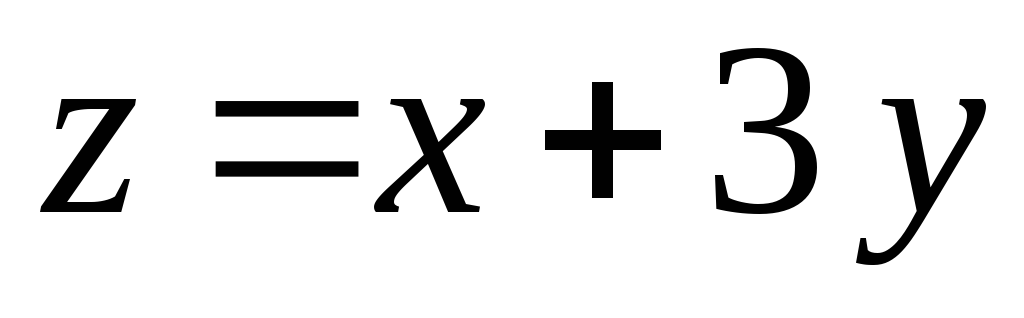 при условии
при условии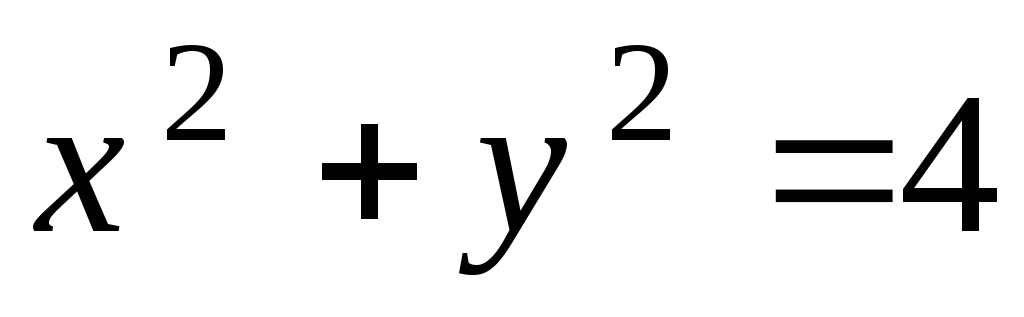 .
.Найти экстремум функции
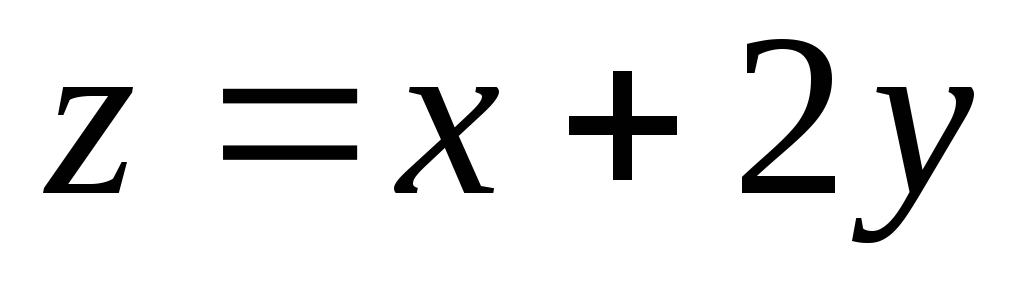 при условии
при условии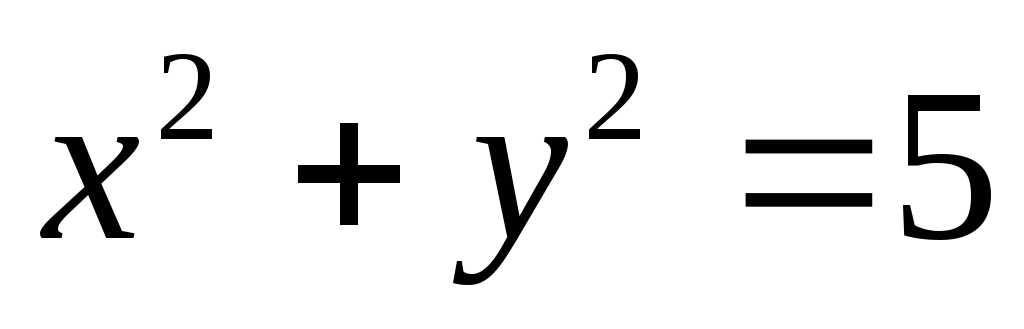 .
.С
 формулируйте
необходимые условия существования
экстремума функции
формулируйте
необходимые условия существования
экстремума функции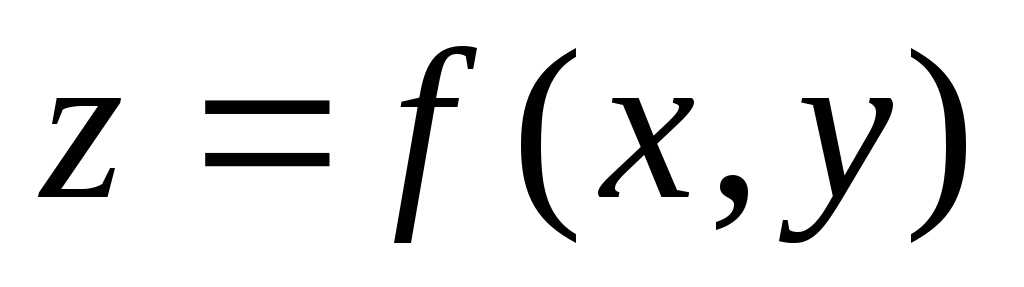 .
Являются ли эти условия достаточными?
Если нет, сформулируйте и проверьте
выполнение достаточных условий
существования экстремума функции
.
Являются ли эти условия достаточными?
Если нет, сформулируйте и проверьте
выполнение достаточных условий
существования экстремума функции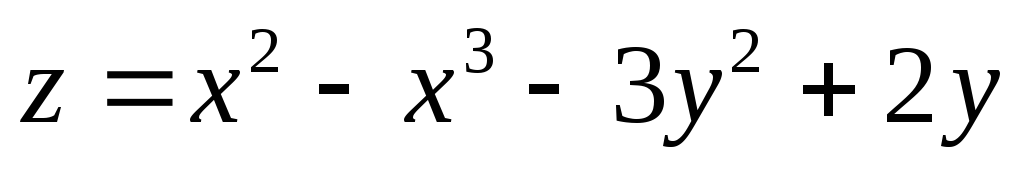 в точке
в точке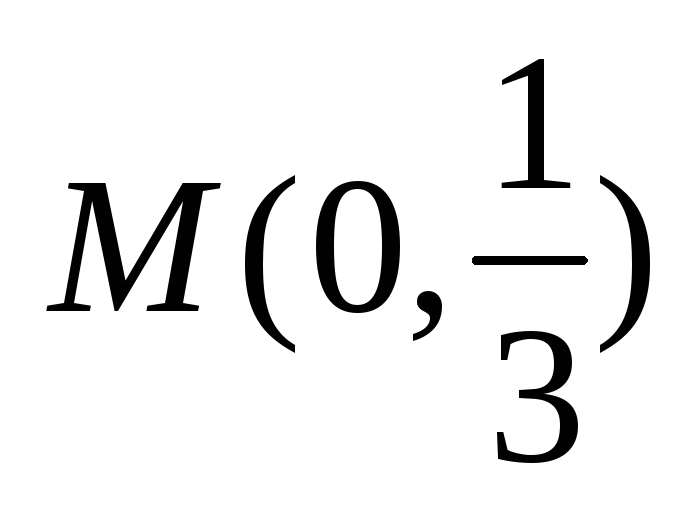
Графически найдите наибольшее значение функции
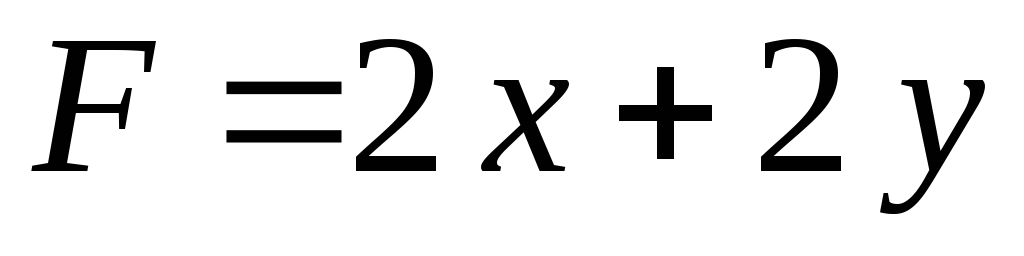 в области, заданной системой неравенств
в области, заданной системой неравенств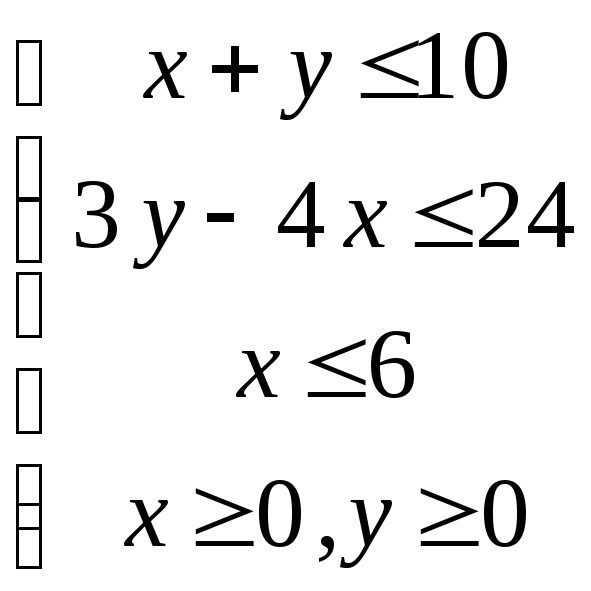 .
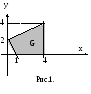
.Графически найдите наибольшее и наименьшее значения функции F = x2 – y в области G , изображенной на рис.1.
Исследовать на экстремум функцию z = xy при условии х2 + у2 = 2а2.
Найти экстремум функцию
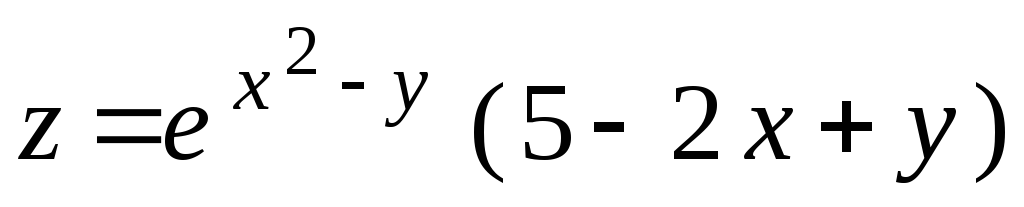 .
.Пусть в качестве эмпирической зависимости выбрана формула
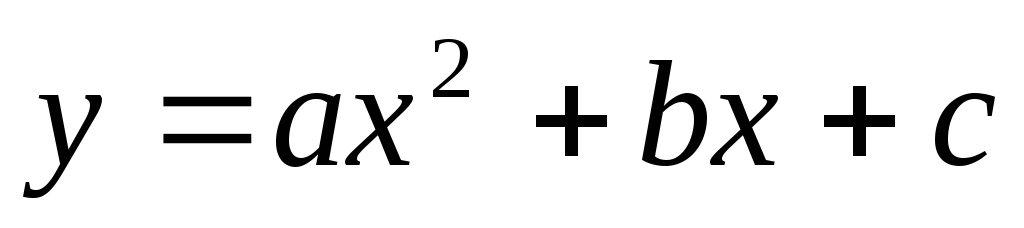 .
Изложите метод нахождения ее неизвестных
параметров.
.
Изложите метод нахождения ее неизвестных
параметров.
