Модуль 2. векторы и аналитическая геометрия
6 Недель, 3 лекции, 6 практич. Занятий
-
Векторы на плоскости 2 ч
-
Прямая на плоскости 2 ч
-
Взаимное расположение прямых. Графическое решение систем линейных неравенств 2 ч
-
Кривые второго порядка 2 ч
-
Контрольная работа № 2 «Векторы и аналитическая геометрия» 2 ч
-
* Задачи с экономическим содержанием 2 ч
Практическое занятие 7.
Векторы на плоскости
Задачи для решения на занятии
Векторы и их координаты
№1.
1) Построить
векторы
,
имеющие общее начало (в любой точке).
2)
Построить
векторы
и
по правилу
треугольников и правилу параллелограмма.
№2.
Даны точки
,
,
.
-
Построить векторы
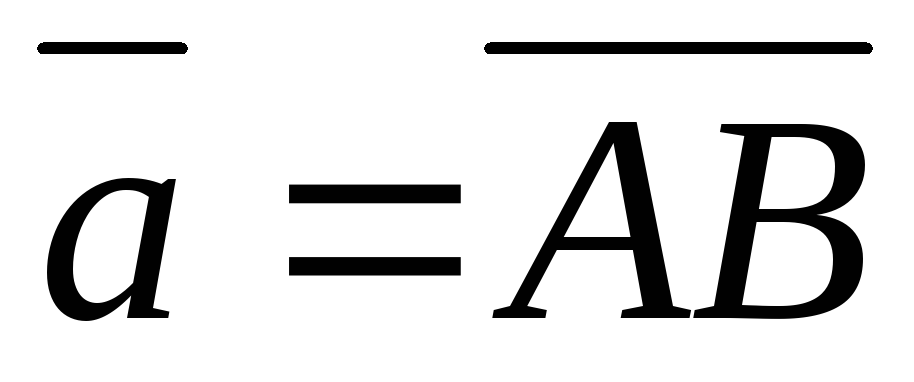и
.
-
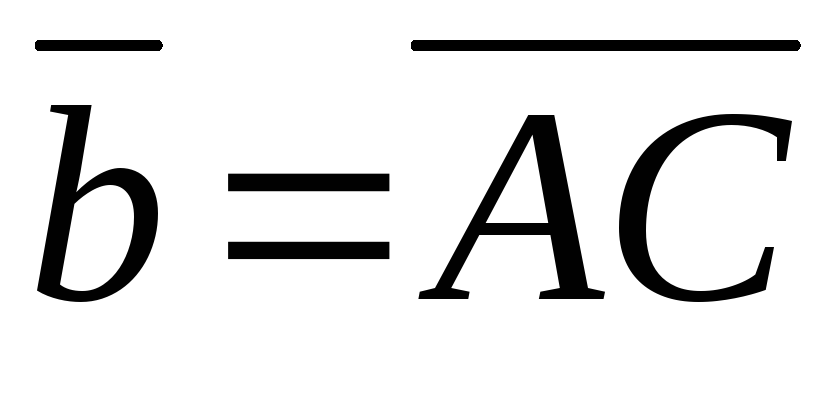Найти координаты векторов
,
,
. -
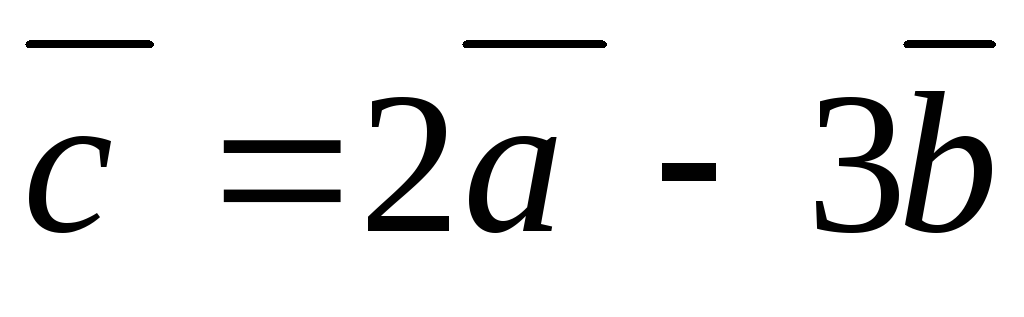Вычислить длины векторов
,
,
.
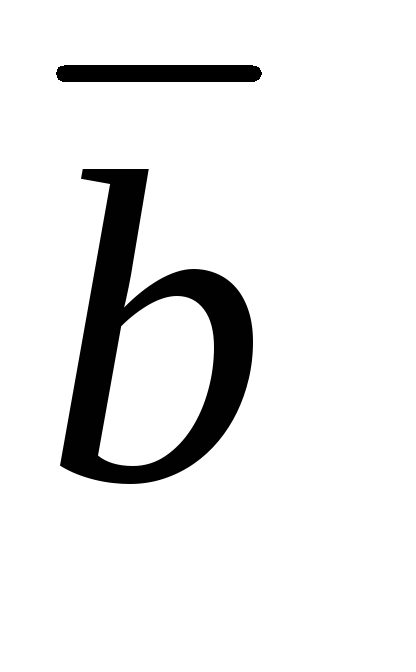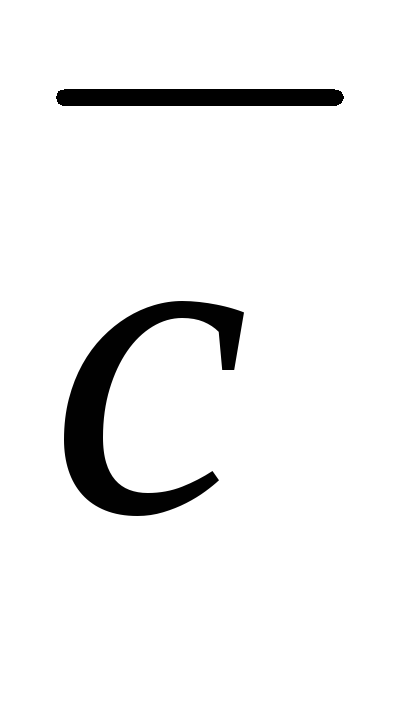№3.
Даны векторы
.
Определить
аналитически (без построения векторов),
какие векторы коллинеарные.
Скалярное произведение векторов
№4.
Вычислите скалярное
произведение
векторов
и
,
если
,
,
а угол между ними равен
.
№5.
Вычислите
скалярное
произведение
векторов, если
,
.
№6.
При каком
значении
вектора
и
перпендикулярны, если
,
.
Задачи для домашнего решения
№7.
Начертите
3 неколлинеарных вектора
.
Постройте векторы:
а)
(по правилу треугольников),
б)
(по правилу параллелограмма),
в)
.
№8.
Построить
векторы
,
с началом в точке
.
№9.
Даны векторы
,
,
.
Построить
.
№10.
Даны точки
,
,
.
-
Найти координаты векторов , , , .
-
Вычислить длины векторов
и
.
№11.
Даны векторы
,
,
.
Определить
аналитически (без построения векторов),
какие векторы: 1)
коллинеарные; 2)
ортогональные?
№12.
Вычислите
скалярное произведение векторов
и
,
если
,
,
а угол между ними равен
.
№13.
Вычислите
скалярное произведение векторов
и
,
если
,
.
Практическое занятие 8.
прямая на плоскости. уравнения прямой
Задачи для решения на занятии
Уравнение линии на плоскости
№1. Принадлежат ли точки
и
линиям, заданным следующими уравнениями?
1)
;
2)
.
№2. Обосновать, какие уравнения задают прямую на плоскости?
(
)
,
(
)
,
(
)
,
(
)
,
(
)
.
№3. Дано уравнение прямой
.
Найти по две точки
и
,
которые лежат на прямой.
Уравнение прямой с угловым коэффициентом
№4. Прямая на плоскости задана
уравнением
.
Найти:
-
угловой коэффициент прямой;
-
координаты точек пересечения прямой с осями ОХ и ОУ. Построить прямую.
№5. Построить прямые, заданные
уравнениями вида
,
если:
1)
,
;
2)
,
; 3)
,
.
Общее уравнение прямой
№6. Прямая на плоскости задана
уравнением
.
1) Записать координаты нормального
вектора
данной прямой.
2) Найти координаты точек пересечения прямой с осью ОХ и осью ОУ.
3) Построить прямую и нормальный вектор.
№7. Прямая проходит через точку
и перпендикулярна вектору
.
1) Составить общее уравнение прямой.
2) Построить прямую и вектор.
Уравнение прямой, проходящей через
две заданные точки
№8. Составить уравнение прямой,
проходящей через точки
и
.
Записать уравнение:
1) в общем виде
;
2) с угловым коэффициентом
.
Задачи для домашнего решения
№9. Прямая на плоскости задана
уравнением
.
Найти:
-
угловой коэффициент прямой;
-
координаты точек пересечения прямой с осями ОХ и ОУ. Построить прямую.
№10. Дано общее уравнение прямой
.
-
Записать координаты нормального вектора
данной прямой.
-
Найти координаты точек пересечения прямой с осью ОХ и осью ОУ.
-
Построить прямую и нормальный вектор.
№11. Составить уравнение прямой,
проходящей через точки
и
.
Записать уравнение:
-
в общем виде
,
-
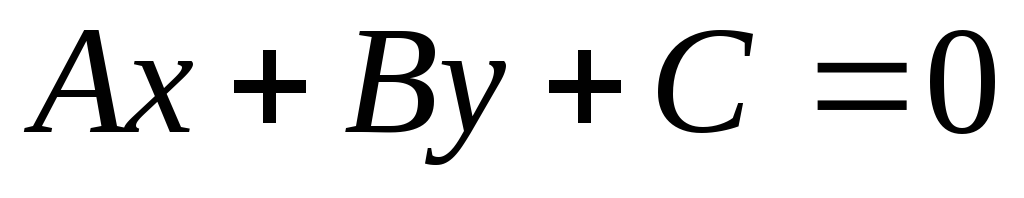2) с угловым коэффициентом
.
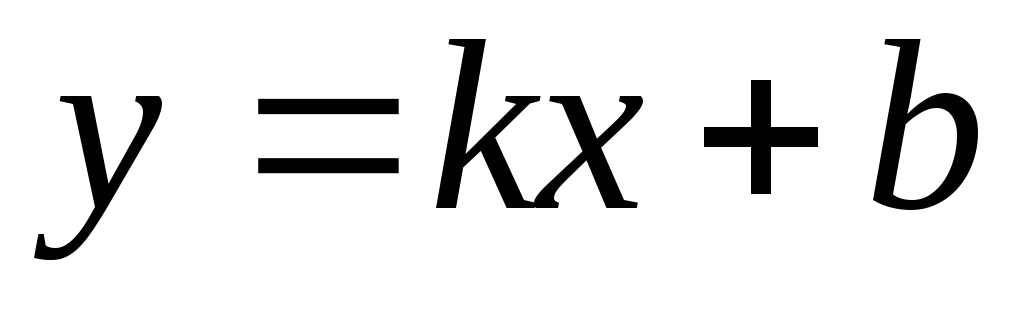Построить прямую.
№12. Составить уравнения трех прямых,
каждая из которых проходит через точку
и:
-
перпендикулярна вектору
;
-
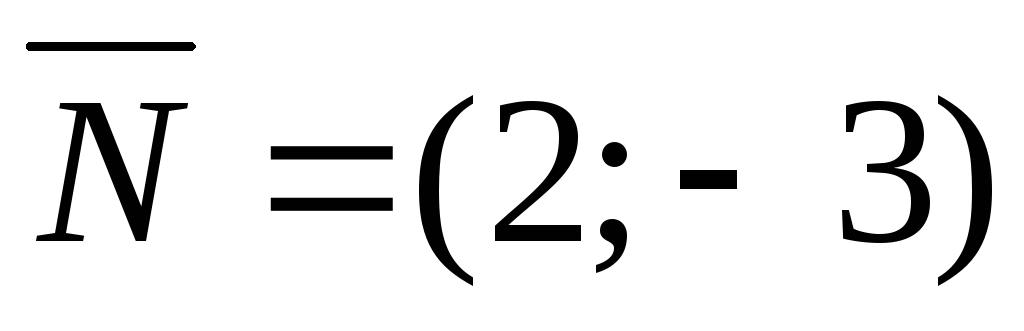параллельна оси ОУ;
-
параллельна оси ОХ. Построить все прямые.
Практическое занятие 9.
взаимное расположение прямых на плоскости. графическое решение систем линейных неравенств
Задачи для решения на занятии
Взаимное расположение прямых на плоскости
№1. Пояснить, почему заданные прямые параллельны.
1)
и
;
2)
и
.
№2. Пояснить, почему заданные прямые пересекаются.
1)
и
;
2)
и
.
№3. Установить, что прямые
и
пересекаются. Найти координаты точки
пересечения прямых. Проверить ответ
графически.
№4*. Составить уравнение прямой,
проходящей через точку
параллельно прямой
.
Построить обе прямые.