Пособие_Физика_часть2
.pdf
Тогда давление газа определяют по формуле
P = |
F |
= |
p |
= |
1 m nv2 . |
(1) |
|
S |
t S |
||||||
|
|
|
3 0 |
|
С точки зрения МКТ давление газа есть импульс, передаваемый его молекулами единице поверхности сосуда в единицу времени.
Молекулы газа движутся с различными скоростями, поэтому в
выражении |
(1) должна стоять средняя скорость |
v |
= ∑v / N , но при этом |
|
|
|
ср |
i |
i |
|
|
|
|
|
к более |
точному значению приводит |
квадратичное усреднение |
||
v
= N1 
∑i vi2 :
P = 13 m0n < vкв >2 .
Уравнение (2) – основное уравнение МКТ. Учитывая, что уравнение (2) можно записать в виде:
РV = 13 m0 N < vкв >2 = 13 m < vкв >2
или РVm = 13 M <vкв >2 .
С учетом уравнения (6) (см. предыдущий вопрос) получают
<v |
кв |
>= |
3kN AT |
= |
3kT |
= |
3RT |
. |
|||
|
|
|
|||||||||
|
|
m0 N A |
|
|
m0 |
|
|
M |
|||
|
|
|
|
|
|
|
|||||
Для воздуха ( M = 29 10−3 кг/ моль ) |
< v |
кв |
>≈ 500м/ с. |
||||||||
|
|
|
|
|
|
|
|
|
|
||
(2)
n=N/V,
(3)
(4)
Средняя кинетическая энергия поступательного движения одной молекулы:
<ε >= |
m0 < vкв >2 |
= |
E |
= |
3 kT . |
(5) |
|
N |
|||||
2 |
|
|
2 |
|
||
С учетом уравнения (5) основное уравнение МКТ можно записать в следующем виде:
P = |
1 |
|
2 |
nm0 < v |
кв |
>2 |
= |
2 |
n < ε >. |
(6) |
|
3 2 |
3 |
||||||||||
|
|
|
|
|
|
||||||
При Т=0 К поступательное движение молекул прекращается и газ не оказывает давления на сосуд.
Контрольные вопросы
1.Выведите основное уравнение молекулярно-кинетической теории
(МКТ)?
2.Что такое средняя квадратичная скорость?
3. Чему равна средняя кинетическая энергия поступательного движения одной молекулы?
22. ЗАКОН РАСПРЕДЕЛЕНИЯ МОЛЕКУЛ ПО СКОРОСТЯМ И ЭНЕРГИЯМ ТЕПЛОВОГО ДВИЖЕНИЯ (РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА)
Несмотря на то, что скорости всех молекул в процессе хаотического движения непрерывно меняют значения и направления, средняя скорость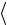 
vкв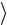
остается постоянной при данной температуре (одна из статистических,
проявляющихся при наличии большого числа частиц в системе, закономерностей). Это объясняется тем, что в состоянии равновесия реализуется некоторое стационарное распределение молекул по скоростям, подчиняющееся определенному статистическому закону. Этот закон был получен Дж.К. Максвеллом (1831–1879) на основе теории вероятности. Функция (распределения Максвелла молекул по скоростям) f(v) определяет относительное число (долю) молекул dN/N, скорости которых находятся в интервале [v,v+dv]:
|
|
|
m0 |
|
3 |
2 |
|
|
|
|
|
− m0v 2 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
v |
2 |
e 2kT . |
|
|||||||||||
f |
(v) = 4π |
|
|
|
|
|
(1) |
|||||||||
|
|
|
|
|||||||||||||
f(v) |
|
|
2πkT |
|
|
|
|
|
|
|
|
|
|
|
||
T1<T2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
dS= |
dN(v) |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dv |
|
|
v |
|
|
vв<v<<vкв< |
|
|
|||||
|
|
|
|
|||||
|
|
|
|
Рис. 1 |
|
|
|
|
По сути, функция распределения молекул по скоростям f(v) равна вероятности dW встречи в газе молекулы со скоростью, заключенной в интервале [v,v+dv]:
|
dN |
dW |
|
||
f (v) = |
|
= |
|
. |
(2) |
N dv |
dv |
||||
Вероятность же встречи молекулы |
со скоростью |
из интервала |
|||
(− ∞;+∞)– событие достоверное – равна 1, т.е. |
|
||||
|
+∞ |
|
|
|
|
|
∫ f (v)dv = 1 . |
(3) |
|||
−∞
Уравнение (3) – условие нормировки.
Функция распределения всегда однозначна (вероятность не может иметь несколько значений для данного значения какого-то параметра), конечна (вероятность конечное число).
Подробнее о статистических закономерностях и функциях распределения см. далее по курсу.
Максимум зависимости (и вероятности) f(v) (рис. 1) будет соответствовать наиболее вероятному значению скорости vв. Данное значение можно получить, исследуя уравнение (1) на экстремум:
|
|
|
m |
0 |
v2 |
|
|
− |
m0v2 |
|
|
|
|
|
− |
m0v2 |
|
d |
|
− |
|
|
|
|
|
|
|
|
m |
|
|
|
|||
|
|
|
2kT |
+ v2 |
|
2kT |
|
||||||||||
|
|
|
|
|
|
||||||||||||
|
v2e |
|
2kT |
|
= 0 , откуда 2ve |
|
|
|
− |
0 |
e |
|
2v = 0 , |
||||
|
|
|
|
|
|
||||||||||||
dv |
|
|
|
|
|
|
|
|
|
|
|
2kT |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
что возможно при трех значениях:
v = 0 , v = ∞ (min функции) |
и |
m0 v2 |
|
= 1 (max |
функции – наиболее |
|
2kT |
|
|||||
|
2kT |
|
|
|
|
|
вероятная скорость), т.е. vв = |
|
|
|
|
|
|
m0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
vв |
= |
2RT . |
(4) |
|
|
|
|
|
|
M |
|
Для получения средней скорости используют методику, принятую в
|
|
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
статистической физике: < g(x) >= ∫xf (x)dx . Подставляя x=v, f(x)=f(v) и dx=dv |
||||||||||||||||||
∞ |
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( < v >= ∫vf (v)dv ) и интегрируя с использованием табличного интеграла |
|
|||||||||||||||||
0 |
|
∞ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 dx = |
1 |
|
|
|
|
|
|
|
|
|||||
|
|
∫x3e−αx |
|
, |
|
|
|
|
(5) |
|||||||||
|
|
2 |
|
|
|
|
|
|||||||||||
|
|
0 |
|
|
|
|
|
|
|
2α |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получают среднюю скорость: |
|
|
|
|
|
|
|
m0v2 |
|
|
|
|
|
|
|
|||
∞ |
|
|
m0 |
3 |
2 |
|
− |
|
|
|
8RT |
|
|
|
||||
< v >= ∫v |
3 |
|
e |
|
|
|
|
|
|
|
|
|||||||
|
4π |
|
|
|
|
|
|
2kT |
|
dv = |
|
|
|
. |
(6) |
|||
|
|
|
|
|
|
π |
M |
|
||||||||||
0 |
|
|
2π kT |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Из формул (4, предыдущий |
вопрос), |
(4) |
и |
|
(6) следует, |
что |
||||||||||||
< vкв >≈ 1,22vв; < v >≈ 1,13vв |
(рис. 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для получения функции распределения молекул по энергиям (ε)
необходимо в равенстве dN (v(ε )) = Nf (v(ε ))dv |
с использованием (5) |
|||||||
провести, исходя из уравнения ε = |
m0 v2 |
, замены v = |
|
2ε |
; dv = |
dε |
. |
|
|
|
2m0ε |
||||||
|
||||||||
2 |
|
|
m0 |
|
||||
Тогда |
|
|
|
|
|
|
m0 |
|
2ε |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
m0 |
|
32 2ε |
|
− |
|
|
|
1 |
|
|
|
4 |
1 |
|
32 |
|
|
|
− |
ε |
||||||||||
|
2kT |
m |
|
|
|
|
|
|
|
1 2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
f (v(ε ))dv = 4π |
|
|
|
|
e |
|
|
|
0 |
|
|
|
|
dε |
= |
|
|
|
|
|
|
ε |
|
e |
|
kT dε |
|||||
|
|
m0 |
|
|
|
|
2m0ε |
2π |
|
|
|
|
|||||||||||||||||||
|
2πkT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
kT |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
dN(ε ) |
|
|
|
2 |
|
|
|
|
|
− |
ε |
|
|
|
|
|
|
|
|
|
|
|
|||
и |
|
|
|
|
|
|
|
|
|
−3 2 |
|
1 2 |
kT |
. |
|
|
|
|
|
|
(7) |
||||||||||
|
|
|
f (ε ) = |
Ndε |
= |
|
|
π |
(kT ) |
|
ε |
|
e |
|
|
|
|
|
|
|
|
|
|
|
|||||||
Находя среднее значение энергии аналогично (6), получают (1, вопрос
19): ε = 32 kT .
Контрольные вопросы
1.Чем характеризуется равновесное состояние газа?
2.Запишите функции распределения молекул по скоростям и энергиям Дж.Максвелла, поясните их смысл. Нарисуйте поясняющие графики.
3.Запишите формулы для средней, средней квадратичной и вероятной скорости молекул.
4.Как связаны между собой универсальная газовая постоянная, постоянная Больцмана и постоянная Авогадро.