Пособие_Физика_часть2

где Ii – момент инерции i–го элемента.

Суммируя (интегрируя) по всем элементам, получают:

С учетом формул (5) и (8) получают еще одну форму записи основного уравнения динамики вращательного движения:

где ε – угловое ускорение.

Переход (*) в формуле (9) справедлив, если конфигурация системы (форма и размеры ТТ, положение оси) остается постоянной, тогда момент инерции I≠ƒ(t)=const.

Пример. Вал массой m и радиусом R вращался с частотой n. К цилиндрической поверхности вала прижали тормозную колодку с силой F, под действием которой вал остановился спустя время t. Определить коэффициент трения f.

Решение. Вал (сплошной цилиндр, рис. 5), участвуя во вращательном движении,

Fтр

x

Рис. 5

При вращении ТТ (системы материальных точек) необходимо учитывать только внешние силы, так как внутренние силы взаимодействия двух любых элементов ТТ (системы) всегда равны по модулю (величине) и противонаправлены вдоль одной прямой (их векторная (геометрическая) сумма равна нулю). Согласно уравнению (6), для замкнутой системы имеем:

Решение. Трением пренебрегают, т.е. в системе не будет неконсервативных сил. Для нее выполняется закон сохранения механической энергии. Так как цилиндр движется без проскальзывания, то угловая скорость его вращения вокруг своей оси симметрии и линейная скорость точек на ободе, равная по модулю скорости поступательного движения его центра масс, связаны соотношением ω=ν/R и, следовательно,

Гироскоп (Г) – с греческого языка можно перевести словами: круг, кружусь, вращаюсь и смотрю, наблюдаю. В широком смысле под гироскопом понимают обладающее большим моментом инерции быстро вращающееся ТТ, ось вращения которого может изменять свое положение в пространстве. Простейший пример гироскопа – детский волчок или юла, у которых нижний конец оси не закреплен, поэтому она может изменять свое положение в пространстве. Если гироскоп обладает симметрией и ось вращения проходит через центр инерции (масс) С тела, то он называется астатическим (уравновешенным), в противном случае – тяжелым.

В технике, в основном, применяют уравновешенные Г, у которых

свободный поворот оси Г обеспечивают, закрепляя его, например, в рамках (кольцах) карданова подвеса (рис. 7, 8), позволяющего оси занять любое положение в пространстве.

Рис. 7

Гироскоп характеризуется двумя свойствами:

1)ось Г стремится сохранить в пространстве приданное ей направление;

2)если на ось начинает действовать сила (пара сил), то Г будет отклоняться в направлении, перпендикулярном плоскости действия силы

(сил).

Это происходит потому, что момент сил всегда направлен перпендикулярно плоскости, в которой лежат сила и ее плечо. В результате Г

вокруг оси ОО/.

Контрольные вопросы

1.Что называется моментом силы относительно точки и оси? Сделайте рисунок и поясните его.

2.Запишите все формулы для нахождения момента силы.

3.В чем измеряется момент силы?

4.Какие условия должны выполняться, чтобы тело находилось в состоянии равновесия?

5.Что называется главным моментом сил?

6.Что называется главными осями инерции тела?

7.Что называется моментом импульса тела относительно точки и оси? Сделайте рисунок и поясните его. Может ли тело, движущееся поступательно обладать моментом импульса?

8.Запишите все формулы для нахождения момента импульса. Как связаны между собой момент силы и момент импульса?

9.В чем измеряется момент импульса?

10.Сформулируйте и запишите математически закон сохранения момента импульса.

11.Запишите формулу для кинетической энергии вращения. Чему равна полная кинетическая энергия движущегося тела?

12.Что такое гироскоп? Что называется гироскопическим эффектом (см. свойства гироскопа)?

13.Что называется прецессией?

14.Сделайте рисунок с пояснениями и выведите формулу для скорости прецессии гироскопа.

13. НЕИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА. СИЛЫ ИНЕРЦИИ. ВЕС ТЕЛА И НЕВЕСОМОСТЬ

Как известноG , в ИСО выполняются законы Ньютона и форма записи

II закона – F = maG. Найдем теперь форму записи для неинерциальной системы отсчёта (неИСО), т.е. СО, движущейся относительно любой ИСО с ускорением. Ограничимся при этом нерелятивистским рассмотрением (m=const при v<<c, с – скорость света в вакууме).

Пусть относительно неподвижной СО S с началом отсчета в точке О тело (масса m) движется с ускорением a , а относительно движущейся поступательно с ускорением a СО S1 с началом отсчета в точке О1 тело

являются силами в привычном смысле этого слова, т.е. они фиктивны. С другой стороны, их можно представлять как действие на тела каких-то силовых полей и реально использовать это на практике. Часто при рассмотрении задач трудно разделить результирующую силу на силу инерции и «ньютоновскую» силу.

Пример. Рассмотрим силу инерции, действующую на тело, покоящееся в движущейся поступательно СО: поезд в метро разгоняется на горизонтальном участке с ускорением а=5 м/с2. Кота, оказавшегося в поезде, согнали с места, и он остался сидеть, прислонившись спиной к стенке, с обиженным выражением глядя по направлению движения (рис.2). Какова перегрузка кота, находящегося в поезде?

Решение. Перегрузкой называется отношение силы F, действующей на кота, к силе

тяжести Р=mg. Кот в неИСОG , связанной с поездом, покоится, а в ИСО относительно земли движется с ускорением Gа. Противоположно направлению движения (ускорению) на кота

действует сила инерции Fu = −maG, вжимающая кота в стенку, ее компенсирует сила реакции

опорыстенки NG1 = maG0 , действующаянакота. ТогдавпроекцияхII законНьютона:

OX: N1 = ma , OY: N = mg .

Силу инерции, действующую на тело, покоящееся во вращающейся СО (рис. 3), называют центробежной (направлена противоположно ускорению). Она направлена противоположно

центростремительной силе, создаваемой натяжением шнура.

Для шарика II закон Ньютона в проекциях на оси будет иметь вид:

ОХ: Fц=Тsinα=man=-Fu,

где r – расстояние от оси вращения.

Fц Fи mg

Рис. 3

Еще одной разновидностью сил инерции является сила Кориолиса

(1792–1843). Она возникает только тогда, когда СО S1 (рис. 1) вращается, а тело движется относительно этой СО. Если рассмотреть движение незакрепленного шарика массы m из центра вращающегося с угловой скоростью ω диска, то его траектория – кривая 12 (рис. 4).

1 2

ω

Рис. 4

Если же дать шарику возможность катиться (трением пренебрегаем) из центра прямолинейно по глубокому желобу, вырезанному вдоль одного из радиусов диска, то шарик, отклоняясь влево от направления движения вдоль

желоба, будет давить на его стенку с силой Fk (рис. 5), названной кориолисовой

(уравновешивается силой реакции опоры стенки желоба FG ). Эта сила определяется выражением

Сила Кориолиса отличается от других сил тем, что зависит от относительной скорости тела во вращающейся СО S1. При обращении в нуль этой скорости, обращается в нуль и сила Кориолиса. То есть, если тело покоится во вращающейся СО, то на него действует (см. рис. 3) центробежная сила инерции, а если движется – то еще и кориолисова сила.

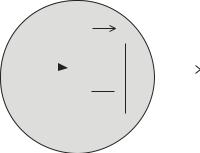
Fk

ω v F

Рис. 5

Действием силы Кориолиса объясняется подмывание (обрывистость) правых берегов рек, текущих в океан с юга на север в северном полушарии.

Размышления о свойствах движения в ИСО и неИСО привели А.Эйнштейна к мысли о независимости движения тел в поле сил инерции от их массы, что наблюдается и в гравитационном поле, и формулированию одного из важнейших принципов физики – принципа эквивалентности: свойства движения в неИСО такие же, как и в ИСО при наличии гравитационного поля (т.е. поля сил инерционных и гравитационных эквивалентны – равноускоренная СО эквивалентна однородному гравитационному полю).

Таким образом, если тело двигается равноускоренно под действием гравитационного поля в ИСО, то, переходя в неИСО, где тело покоится, получаем, что его уравновешивает сила инерции. При данном переходе изменяется геометрия пространства – времени, что изучается в общей теории относительности (ОТО) А.Эйнштейна.

Весом тела называется приложенная к телу сила РG, с которой это тело действует на опору или подвес. При этом предполагается, что опора или подвесG покоятся в системе отсчета, в которой взвешивают тело. В среднем P = mgG0 , в общем случае вес – есть геометрическая сумма силы

гравитационного притяжения Земли и центробежной силы инерции, вызванной ее вращением.

При ускоренном движении системы могут возникнуть особые состояния, называемыеперегрузками(см. рис. 2 ипример) иневесомостью.

Вспомним известную со школы задачу о лифте (рис. 6). При сонаправленности ускорения движения лифта а и ускорения свободного падения gG вес тела P=N=m(g-a), т.е., если лифт движется с ускорением a=g,

то Р=0. Это состояние называют невесомостью. Если же ускорения

противонаправлены, то P=N=m(g+a). Увеличение веса приводит к

перегрузкам.

Тяжелые перегрузки и невесомость в повседневной жизни – состояния редкие (быстрая езда в транспорте, полет на самолете, катание на качелях, подъемы и спуски в лифтах), с ними часто приходится сталкиваться лишь космонавтам, которых специально тренируют на центрифугах и в бассейнах для привыкания к состояниям деформации внутренних органов и изменениям внутреннего давления. В космических кораблях невесомость (движение с ускорением свободного падения) может быть компенсирована путем создания вращения корабля (действием сил инерции), при этом предметы вновь обретут вес, который будет зависеть от скорости вращения.

Контрольные вопросы

1.Что называется инерциальной и неинерциальной системой отсчета? В каких системах отсчета выполняются законы Ньютона?

2.Какие величины называют абсолютными, относительными и переносными?

3.Что такое сила инерции?

4.Какую силу называют кориолисовой? Запишите формулу.

5.Сформулируйте принцип эквивалентности.

6.Что называется весом тела, невесомостью? Как изменяется вес тела в лифте? Запишите второй закон Ньютона в проекциях на оси для человека в лифте и найдите его вес в различных случаях.

7.Что называется перегрузкой?

14.ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ