Методические указания к выполнению индивидуальных домашних заданий

1. Элементы линейной алгебры. Матрицы и действия с матрицами

Матрицей размера называется прямоугольная таблица чисел

,

имеющая строк истолбцов.

Элементы матрицы снабжаются двумя индексами, первый из которых обозначает номер строки, второй - номер столбца, на пересечении которых стоит элемент. Если матрица имеетстрок истолбцов, то матрицу называют квадратной.

Матрицы одинакового размера можно складывать. При этом суммой матриц иназывают матрицу, для которой.

Например,

.

Произведением матрицы 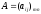на числоназывают матрицу, каждый элемент которой. Например,

.

Задача. Даны матрицы и:

; .

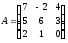Найти матрицы: a) , б) .

Решение. а) ; ;

;

б) ;;

.

Произведением 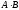матрицыразмеромна матрицуразмеромназывают матрицуразмером, каждый элемент которой, где;.

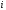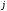То есть элемент –ой строки и–го столбца матрицы произведенияравен сумме произведений элементов–ой строки матрицына соответствующие элементы–го столбца матрицы.

Если определено произведение, то это не значит, что определено произведение. Это произведение может не иметь смысла. Если выполняется, то матрицы называются перестановочными, или коммутирующими. Отметим сразу же, что обычно.

Задача. Даны матрицы и:

; .Найти матрицу.

Решение.

⁼⁼

.

Обратные матрицы

Квадратная матрица называется обратимой, если существует матрицатакая, что. Эту матрицу называют обратной к матрицеи обозначают.

Условием существования матрицы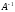, обратной к квадратной матрице_, является ее невырожденность (условие , где- определитель, составленный из элементов матрицы).

Алгебраическим дополнением элемента матрицыназывается произведение числана минор- определитель, получающийся при вычеркиванием-ой строки и-го столбца. Например, некоторые элементы матрицы

имеет следующие алгебраические дополнения:

;;;

Если квадратная матрица - не вырождена, то обратная матрица_.

Задача. Решить систему уравнений матричным способом:

Решение. Составим матрицы:

- матрица коэффициентов при неизвестных;- матрица неизвестных;

- матрица свободных членов.

Тогда матричная запись рассматриваемой системы уравнений будет иметь вид . Решение матричного уравнения,

где обратная матрица _.

Найдем определитель матрицы :

.

Алгебраические дополнения _:

;;;

;;;

;;

Обратная матрица .

Решение матричного уравнения:

.

_Ответ:

Задача. Решить систему уравнений методом Крамера:

Решение. Из предыдущей задачи главный определитель системы .

Найдём определитель , который получается из определителя заменой первого столбца столбцом свободных членов.

.

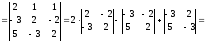
Найдём определитель , который получается из определителя заменой второго столбца столбцом свободных членов, тогда

_{Аналогично:}

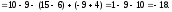
По формулам Крамера решение системы:

, ,

_Ответ:

Задача. Решить систему уравнений методом Гаусса:

Решение. Составим расширенную матрицу системы: слева от черты коэффициенты при неизвестных, справа свободные члены. Приведем расширенную матрицу системы с помощью элементарных преобразований со строками к виду:

_{Обозначим строки матрицы через}

Элементарные преобразования строк следующие:

1.Поменять местами строки .

2.Строку разделить или умножить на число

3.Линейная комбинация строк

Тогда,

Из третьей строки последней матрицы находим:

_{Из второй строки находим:} , откуда

_{Из первой строки находим:} , откуда

_Ответ:

Задача. Решить систему уравнений методом Гаусса:

Решение. Составим расширенную матрицу системы:

Из третьей строки последней матрицы:

_{Из второй строки имеем} Откуда,

_{Из первой строки находим:} Откуда,

Ответ: Система имеет бесконечное множество решений (совместная неопределенная система).

Задача. Решить систему уравнений методом Гаусса:

Решение. Составим расширенную матрицу из коэффициентов матрицы:

Из последней строки находим . Так как деление на ноль невозможно, то данная система не имеет решений.

Ответ: система не имеет решений (несовместная система).