Министерство образования и науки
Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего профессионального образования
Национальный исследовательский ядерный университет «МИФИ»
Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ
ЛИНЕЙНАЯ И ВЕКТОРНАЯ АЛГЕБРА.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Индивидуальные домашние задания и методические указания для их выполнения
по курсу «Математика»
для студентов 1-го курса направления «Машиностроение»
Волгодонск 2014
УДК 811.111-36 (076.5)
Ф 947
Рецензент д.т.н., проф. Сысоев Ю.С.
Составители: Алексеева М.А., Замыслова А.И.,
Лисичкина О.М., Батаков А.И.
Линейная и векторная алгебра. Аналитическая геометрия./ М.А. Алексеева, А.И. Замыслова, О.М. Лисичкина, А.И. Батаков. – ВИТИ НИЯУ МИФИ. – Волгодонск, 2014. – 61 с.
Предназначено для студентов 1-го курса направления «Машиностроение»
© ВИТИ НИЯУ МИФИ, 2014
© Коллектив авторов, 2014
Предисловие.
В целях лучшего усвоения курса математики и интенсификации самостоятельной работы студентов в соответствии с учебными планами на всех направлениях Волгодонского инженерно-технического института (филиала) НИЯУ МИФИ предусмотрено выполнение индивидуальных домашних заданий (ИДЗ).
В настоящей методической разработке представлены индивидуальные задания для студентов 1 курса по разделу «Линейная и векторная алгебра. Аналитическая геометрия».
Номер варианта индивидуален для каждого студента и определяется преподавателем, ведущим практические занятия. Работа выполняется студентом на отдельных листах.
Решение задач студенты представляют в письменной форме с подробным изложением и указанием, используемых при этом, основных теоретических положений. На преподавателя, ведущего практические занятия, возлагается обязанность по систематическому контролю самостоятельной работы студентов, по организации ритмичности в выполнении ими ИДЗ, что снимет дополнительные перегрузки их в конце семестра.
В определённые преподавателем сроки частично или полностью выполненные ИДЗ сдаются на проверку.
Студенты, сдавшие в срок отчёт по ИДЗ, допускаются к сдаче экзамена или зачёта.
1 Даны матрицы a, b, c, числа α и β.
Вычислить: а) C·B; б) α·Α+β·B; в) А-1
1)
α=3; β=5;
2)
α=-4; β=6;
3)
α=8;
β=-2;
4)
α=2; β=3;
5)
α=-2; β=-2;
6)
α=-3; β=-2;
7)
α=5; β=-2;
8)
α=-2;
β=-3;
9)
α=-3; β=3;
10)
α=5; β=2;
11)
α=-4;
β=2;
12)
α=-4; β=-6;
13)
α=-3; β=2;
14)
α=-3;
β=2;
15)
α=-4;
β=3;
16)
α=3;
β=-4;
17)
α=2;
β=5;
18)
α=-5;
β=-5;
19)
α=2;
β=-3;
20)
α=3; β=-2;
21)
α=-3;
β=4;
22)
α=5;
β=4;
23)
α=-2;
β=-3;
24)
α=2;
β=3;
25)
α=-3;
β=2;
26)
α=3;
β=4;
27)
α=-3; β=2;
28)
α=3; β=4;
29)
α=-5; β=-2;
30)
α=-4; β=2.
2 Решить систему линейных уравнений по формулам Крамера, матричным методом, методом Гаусса
|
1)
|
2) |
|
3) |
4) |
|
5) |
6) |
|
7) |
8) |
|
9) |
10) |
|
11) |
12) |
|
13) |
14) |
|
15) |
16) |
|
17) |
18) |
|
19) |
20) |
|
21) |
22) |
|
23) |
24) |
|
25) |
26) |
|
27) |
28) |
|
29) |
30) |
; 
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.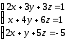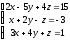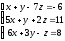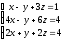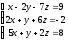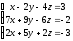