Vse_bomby_s_dokazatelstvami

13. Степенные ряды. Радиус сходимости.

Определение. Функциональный ряд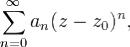

где an и z0 - комплексные числа, а z - комплексная переменная, называется степенным рядом.

Определение. Радиусом сходимости степенного ряда (1) называется число

или 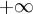: 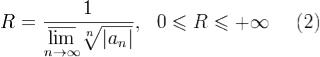кругом сходимости ряда (1) называется круг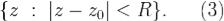

Круг сходимости является открытым множеством. При 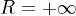он совпадает со всей комплексной плоскостью.

Формула (2) называется формулой Коши-Адамара.

Теорема. Признак Коши. Пусть в 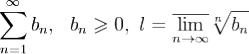. Тогда

1.при l < 1 ряд сходится

2.при l > 1 ряд расходится и даже общий член не стремиться к нулю.

Теорема. Пусть R - радиус сходимости ряда. Тогда

1.при | z | < R ряд сходится и даже абсолютно.

2.при | z | > R ряд расходится и даже общий член не стремится к нулю. Теорема. Пусть R - радиус сходимости степенного ряда, 0 < r < R. Тогда в круге 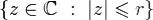ряд сходится равномерно.

Доказательство: 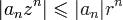- числовой сходящийся ряд.

Бесконечная дифференцируемость суммы степенного ряда.

Пусть R > 0 - радиус сходимости ряда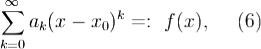

ak - вещественные числа.Тогда при | x − x0 | < R f имеет производные всех порядков, которые находятся почленным дифференцированием; Доказательство.Докажем утверждение, что степенные ряды, полученные почленным дифференцированием или почленным интегрированием, имеют тот же радиус сходимости R.

Радиусы сходимости рядов 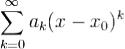и совпадают.

Доказательство. Пусть радиусы сходимости указанных рядов соответственно R и R'. Очевидно, что ряд сходится там же, где 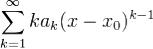, и, следовательно, имеет тот же радиус сходимости R'.

В силу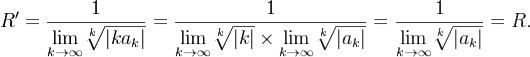 Утверждение следует из 3 и равномерной сходимости ряда.

Ряд Тейлора.

Если функция 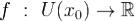определена в некоторой окрестности точки 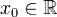и имеет в точке x0производные всех порядков (т.е. является бесконечно дифференцируемой в точке x0), то степенной ряд

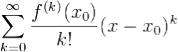называется рядом Тейлора функции f в точке x0.

14. Формула Грина.

Пусть функции P(x,y) и Q(x,y) непрерывно дифференцируемы в односвязной области 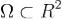, а простой кусочно гладкий контур 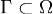ограничивает область . Тогда справедлива формула Грина

где 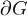есть положительно ориентированная граница области G.

Доказательство.

Докажем сначала формулу (1) в наиболее простом случае, когда

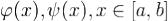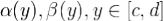область G еще и элементарна относительно обеих координатных осей, т.е. существуют такие кусочно непрерывно дифференцируемые и непрерывные функции , и , что

.

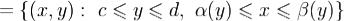Примерами таких областей явл внутренности круга, эллипса, треугольника. Применяя формулу сведения двойного интеграла к повторному, получаем

Добавленные интегралы по вертикальным отрезкам DE и NA равны нулю, так как на этих отрезках x = const. Аналогично доказывается формула

Складывая равенства (2) и (3) получаем формулу Грина (1).

Пусть теперь область G по-прежнему ограничена кусочно гладкой замкнутой кривой 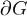. Предположим её можно кусочно гладкой простой кривой Γ разбить на две области простейшего вида рассмотренные выше. Тогда,

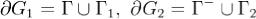Применяя формулу Грина в каждой из областей G1 и G2, получаем при складывание, что интегралы по Γ и Γ− взаимно уничтожается и мы опять приходим к формуле Грина. При помощи математической индукции легко обобщить на случай односвязной области.

Потенциальные векторные поля на плоскости.

Векторное поле , заданное на области , называется потенциальным в области G, если существует непрерывно

дифференцируемая функция 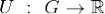такая, что 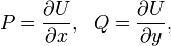на G. Функцию U называют при этом потенциальной функцией поля 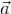или потенциалом поля .

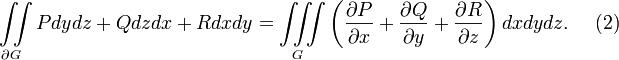
15.Формула Остроградского-Гаусса.

Пусть 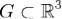- ограниченная область, граница которой 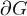есть кусочно гладкая поверхность, ориентированная внешними нормалями.

В 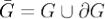задано непрерывно дифференцируемое векторное поле 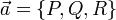. Тогда поток векторного поля 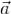через границу области 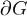равен тройному интегралу от 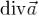по области G, т.е.

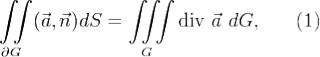, или

Доказательство.Докажем сначала формулу Остроградского-Гаусса в одном важном частном случае, когда область G еще и элементарна относительно всех трех координатных осей. Напомним, что область G называется элементарной относительно оси z, если найдутся две такие непрерывные в замыкании области 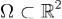функции 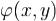и ψ(x,y), что .

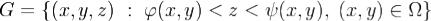Применяя формулу сведения тройного интеграла к повторному, получаем

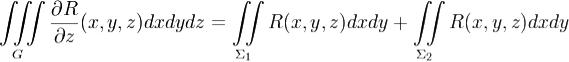.(3) Здесь Σ1 - поверхность, являющаяся графиком функции ψ(x,y), a Σ2 - поверхность, являющаяся графиком функции .

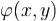Соленоидальные векторные поля.

Кусочно гладкую поверхность, являющуюся границей ограниченной односвязной области, в дальнейшем для краткости будем называть допустимой.Непрерывно дифференцируемое в области G поле 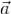будем называть соленоидальным, если поток вектора 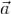через любую допустимую поверхность 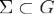равен нулю.

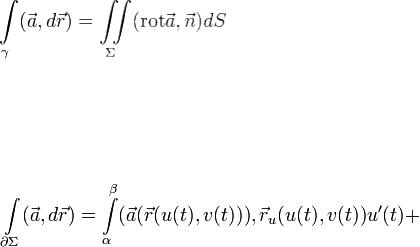
16.Формула Стокса для простой гладкой поверхности.

Пусть в ориентированном евклидовом пространстве задана простая поверхность Σ уравнением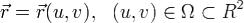.(1)

Здесь Ω - замкнутая область, граница которой есть положительно ориентированный гладкий (или кусочно гладкий) контур (при обходе границы 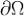область Ω остается слева). Пусть 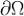задается уравнениями 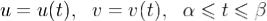.(2)

Образ кривой 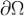при отображении (1) мы назвали положительно ориентированным краем поверхности Σ и обозначили 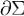. Напомним, что ориентация поверхности Σ, создаваемаяя полем нормалей 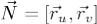, называется согласованной с положительной

ориентацией края. Было показано, что такое согласование совпадает с известным правилом правого винта.

Пусть в окрестности поверхности Σ задано непрерывно дифференцируемое векторное поле 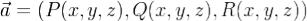. Если γ - замкнутый

контур, то криволинейный интеграл 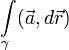в физике называют циркуляцией векторного поля 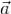по контуру γ. Если 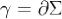, то говорят, что поверхность Σ натянута на контур γ.

Теорема Стокса.Циркуляция векторного поля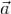по контуру 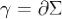равна потоку вихря этого поля через поверхность Σ, натянутую на контур γ, т.е.

Доказательство.Докажем теорему Стокса в тех предположениях, которые были сформулированы в начале. Из (1) и (2) получаем уравнение края поверхности.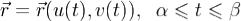

Сводя криволинейные интегралы к определенным, получаем

.

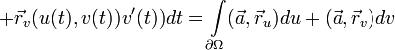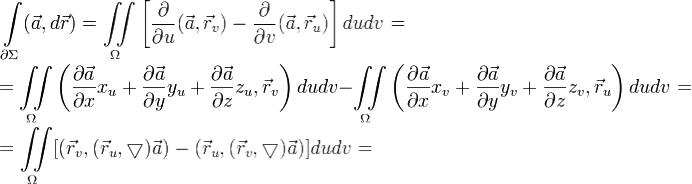
Сделаем дополнительное предположение о непрерывности (а следовательно и равенстве) смешанных производных и . Тогда в силу формулы Грина получаем равенство

.

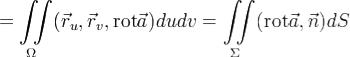Здесь была использована формула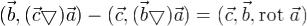 при 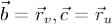, а также формула, выражающая поток через двойной

интеграл от смешанного произведения: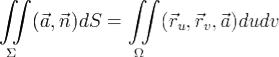. Итак, формула Стокса доказана для простой гладкой поверхности, натянутой на кусочно глакий контур.

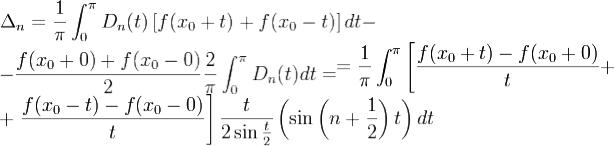
17. Теорема о сходимости ряда Фурье в точке.f - 2π периодическая, абсолютно интегрируемая на[ − π,π] функция.x0 – еёпочти регулярная

точка f.Тогдаряд Фурье в этой точкеx0 сходится к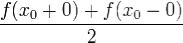. Если же при этом x0 - регулярная точка f, то ряд Фурье в точке x0 сходится

к f(x0).Рассмотрим предел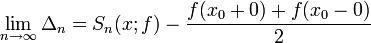

Дробь 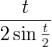, доопределенная единицей в нуле, является непрерывной на [

− π,π] функцией.Дробь 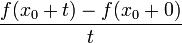абсолютно интегрируема на [ − π,π] функция, поскольку таковой является её числитель, и при 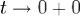она имеет конечный предел.По теореме Римана об осцилляции, последний интеграл стремиться к нулю при , т.е.

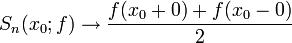при

Следствие.Пусть 2π - периодическая функция f абсолютно интегрируема на отрезке [ − π,π], и существуетf'(x0). Тогда ряд Фурье функции f сх. в x0 к f(x0).

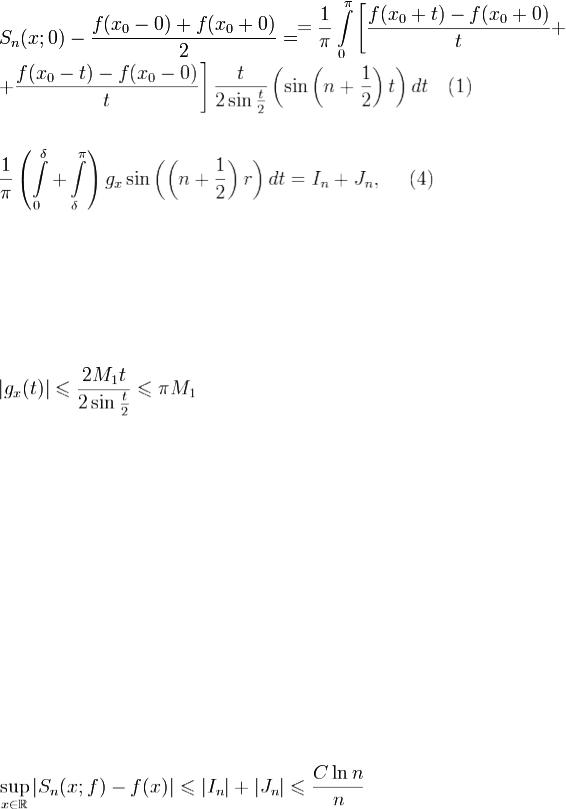
18. Дост. условия равномернойсх-сти тригонометрического ряда Фурье.

Пусть f - 2π периодическя и кусочно непрерывно дифференцируемая функция.Тогда ряд Фурье функции f сходится к f равномерно на 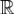и

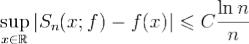при 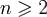,где C не зависит от n. Доказательство. Пусть 0 < δ = δn < π. Перепишем формулу

в виде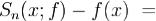

.

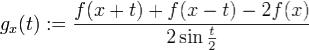Пусть M1 = max | f' | . C помощью теоремы Лагранжа о конечных приращениях получаем, что при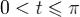

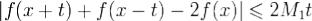.Следовательно, при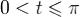

и (за исключением быть может, конечного числа

значений t)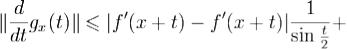

.

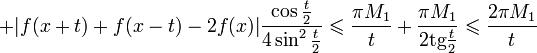Очевидно, что .С помощью интегрирования по частям имеем

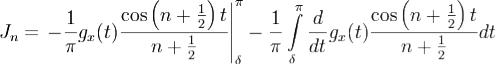. Отсюда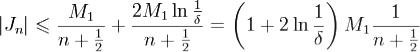. Пологая 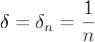, получаем, что при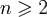

,где C не зависит от n. Доказана.

19. Преобразование Фурье абсолютно интегрируемой на функции есть ограниченная и непрерывная на функция.

Доказательство. Так как функция f(x) абсолютно интегрируема на , то

и, следовательно, 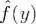есть ограниченная функция на .

Для доказательства непрерывности функции 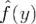запишем её в виде

и заметим, что, в силу леммы 4, $74 функция a(y) и b(y) непрерывны на 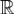. Лемма 4.Если f(x) - абсолютно интегрируемая на 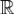функция, то

функции a(y) и b(y), определенные равенствами

Доказательство. Докажем, например, непрерывность a(y). Из уравнения для a(y) следует, что

Так как функция f(t) абсолютно интегрируема, то интервал 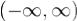можно разбить на три таких интервала 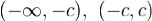и 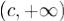, что по бесконечным интервалам интегралы от функции |f(x) | не будут

превышать 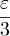. второй итнеграл меньше чем,

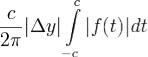и, следовательно, существует δ > 0 такое, что при | Δy | < δ второй интеграл

меньше 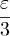. Следует, что при | Δy | < δ приращение .

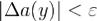Преобр Фурье производной и производная преобразования Фурье.

Если непрерывная и абсолютно интегрируемая на 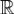функция f(x) является кусочно гладкой на любом отрезке 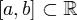, а функция 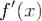абсолютно интегрируема на 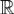, то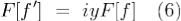.