
Vse_bomby_s_dokazatelstvami
.pdf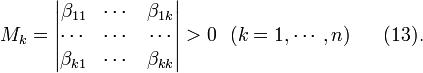
25. Положительно определенные квадратичные формы. Определение. Квадратичную форму k будем называть положительно определенной на подпространстве L'пространства L, если k(x) > 0 для любого ненулевого вектора x из L'.
Если говорят, что квадратичная форма положительно определена без уточнения подпространтсва, то она обладает таким свойством на всем L. Теорема. Для положительной определенности квадратичной формы необходимо и достаточно, чтобы миноры её матрицы удовлетворяли
неравенствам Миноры вида (13) называются главными минорами матрицы.
Доказательство. Для доказательства вспомним преобразования матрицы квадратичной формы, примененные при доказательстве теоремы 1.
1.Необходимость. Если квадратичная форма k положительно определена, то диагональные элементы её матрицы в любом базисе удовлетворяет условиюβii = k(ei) > 0,и, следовательно, при приведении матрицы к диагональному виду особый случай не встретиться. В основном случае к любой строке может быть прибавлена только лежащая выше, а к любому столбцу - только расположенный левее. При таких преобразованиях главные миноры матрицы не изменяться. Но у диагональной матрицы для положительно определенной квадратичной формы главные миноры положительны. Поэтому они положительны и у исходной матрицы.
2.Достаточность. Пусть все главные миноры матрицы B положительны. В частности, M1 = β11 > 0, и первый шаг преобразования приводит матрицу к виду (10) с 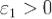 . Допустим, что после k шагов мы получили матрицу Bk с положительными
. Допустим, что после k шагов мы получили матрицу Bk с положительными 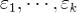 , причем не возникало особого случая. Тогда для
, причем не возникало особого случая. Тогда для
левого верхнего элемента матрицы Ck имеем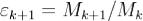 , так как главные миноры не менялись. Поэтому
, так как главные миноры не менялись. Поэтому 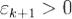 , на очередном шаге преобразования имеет место основной случай и полученная матрица имеет положительные элементы
, на очередном шаге преобразования имеет место основной случай и полученная матрица имеет положительные элементы 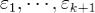 . Рассуждая так для всех k, мы придем к доказательству утверждения.
. Рассуждая так для всех k, мы придем к доказательству утверждения.
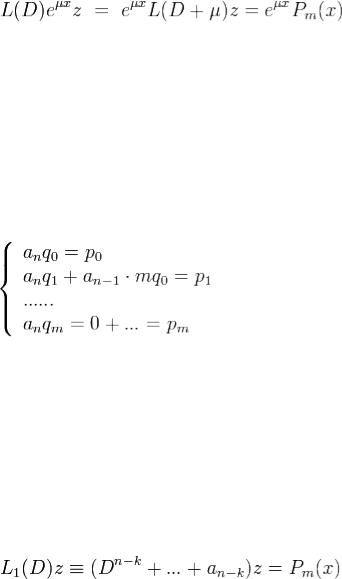
26.Когда правая часть являетсяквазимногочленом.Рассмотрим уравнение 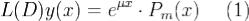 ,гдеμ - заданное комплексное число, Pm(x) - заданный многочлен степени m.
,гдеμ - заданное комплексное число, Pm(x) - заданный многочлен степени m.
Определение. Если число μ является корнем характеристического уравнения L(λ) = 0, то говорят, что в уравнении (1) имеет место резонансный случай.
Теорема. Для уравнения (1) существует и единственно решение вида 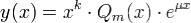 где Qm(x) - многочлен одинаковой с Pm(x) степени m, а число k равно кратности корня μ характеристического уравнения L(λ) = 0 в резонансном случае и k = 0 в нерезонансном.
где Qm(x) - многочлен одинаковой с Pm(x) степени m, а число k равно кратности корня μ характеристического уравнения L(λ) = 0 в резонансном случае и k = 0 в нерезонансном.
Доказательство. Если 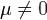 , то заменой
, то заменой 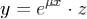 в уравнении (1) всегда можно избавиться от eμxв правой части.
в уравнении (1) всегда можно избавиться от eμxв правой части.
Отсюда 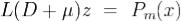 .Таким образом доказательство теоремы осталось провести для уравнения вида
.Таким образом доказательство теоремы осталось провести для уравнения вида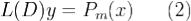
a) Нерезонансный случай: 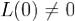 . Пусть
. Пусть 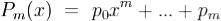 ,
,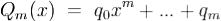 .
.
Подставляя Pm,Qm в уравнениие (2) и приравнивая коэффициенты при одинаковых степенях x, получаем линейную алгебраическую систему уравнений для определения неизвестных коэффициентов q0,...,qm
Матрица этой системы треугольная с числами 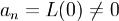 по диагонали,поэтомукоэффициентыQm(x) определяются однозначно.
по диагонали,поэтомукоэффициентыQm(x) определяются однозначно.
б) Резонансный случай: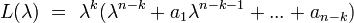
Следовательно 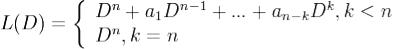
В случае k < n замена Dky = z в уравнении (1) приводит к уравнению
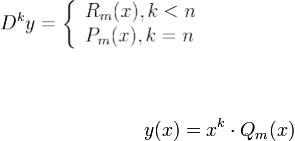
Поскольку 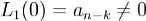 , то для этого уравнения имеет место нерезонансный случай. Следовательно существует, единственное решение этого уравнения z = Rm(x).
, то для этого уравнения имеет место нерезонансный случай. Следовательно существует, единственное решение этого уравнения z = Rm(x).
Рассмотрим уравнение |
|
Взяв нулевые начальные условия для этого уравнения |
|
y(0) = y'(0) = ... = y(k − 1)(0) = 0 |
|
получаем единственное решение вида |
. |
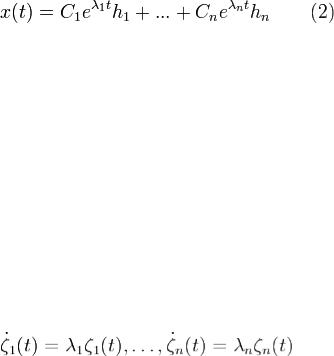
27. Системы линейных однородных уравнений с постоянными коэффициентами, методы их решения.
Рассмотрим нормальную линейную однородную систему 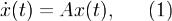 где
где 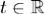 , A - квадратная комплексная матрица порядка n, x(t) - неизвестная вектор-функция с nкомпонентами. Лемма 1. Если x(1)(t),x(2)(t) решения системы (1), а C1,C2 - произвольные комплексные числа, то вектор-функция x(t) = C1x(1)(t) + C2x(2)(t) также решение системы (1).
, A - квадратная комплексная матрица порядка n, x(t) - неизвестная вектор-функция с nкомпонентами. Лемма 1. Если x(1)(t),x(2)(t) решения системы (1), а C1,C2 - произвольные комплексные числа, то вектор-функция x(t) = C1x(1)(t) + C2x(2)(t) также решение системы (1).
Лемма 2. Для того, чтобы вектор-функция x(t) = eλth была нетривиальным решением системы (1), необходимо и достаточно, чтобы λ было собcтвенным значением, а h - соответствующим ему собственным вектором преобразования A.
Доказательство. Будем искать решение (1) в виде x(t) = eλth, где 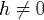 - числовой n - мерный вектор. Подставляя x(t) в систему (1),
- числовой n - мерный вектор. Подставляя x(t) в систему (1),
получим λeλth = Aeλth или Ah = λh.
Теорема. Пусть существует базис 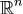 из собственных
из собственных
векторов h1,...,hn линейного преобразования A и пусть λ1,...,λn - соответствующие им собственные значения.Тогда:
а) Вектор-функция x(t) вида
где C1,...,Cm произвольные комплексные постоянные, является решением системы (1).
б)Если x(t) - какое-либо решение системы (1), то найдутся такие значения постоянных C1,...,C2, при которыхx(t) задается формулой (2). Доказательство.а)Утверждение теоремы следует из лемм 1 и 2.
б)Пусть x(t) - какое-либо решение (1). Так как h1,....,hn - базис в 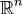 , то для
, то для 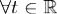 x(t) = ζ1(t)h1 + ... + ζn(t)hn.
x(t) = ζ1(t)h1 + ... + ζn(t)hn.
Подставим x(t) в систему (1). Имеем 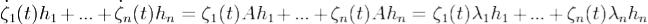 . Так как h1,...,hn - линейно независимые вектора, то отсюда
. Так как h1,...,hn - линейно независимые вектора, то отсюда
Из этих уравнений находим, что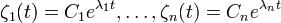 .
.
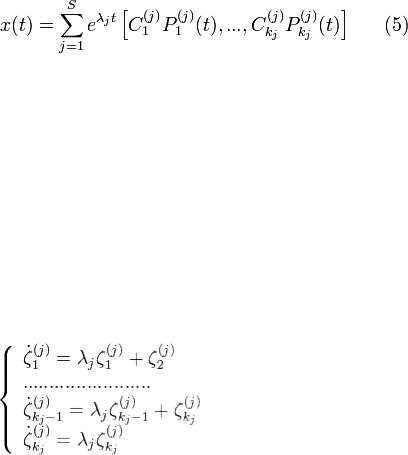
Лемма 3. Каждая из вектор-функций 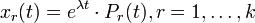 является
является
решением системы (1), где 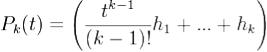 , где
, где  - некоторая жорданова цепочка дляλ.
- некоторая жорданова цепочка дляλ.
Доказательство. При k = 1 утверждение леммы 3 доказано в лемме 2. Пусть 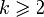 . Тогда
. Тогда 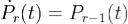 , а из определения жордановой цепочки (3) следует, что APr(t) = λPr(t) + Pr − 1(t). Подставляя xr(t) в систему (1), получаем что
, а из определения жордановой цепочки (3) следует, что APr(t) = λPr(t) + Pr − 1(t). Подставляя xr(t) в систему (1), получаем что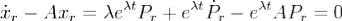 .
.
Теорема. Пусть жорданов базис в 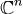 состоит из S жордановых
состоит из S жордановых
цепочек 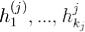 длин kj(k1 + ... + kS =n) для собственных значений λj преобразования A, j = 1,...,S.Тогда:
длин kj(k1 + ... + kS =n) для собственных значений λj преобразования A, j = 1,...,S.Тогда:
а) вектор - функция фида
б) если x(t) - какое-либо решение системы (1), то найдется такой
набор 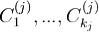 при котором x(t)задается в форме (5). Доказательство.a) следует из принципа суперпозиции и Леммы 3.
при котором x(t)задается в форме (5). Доказательство.a) следует из принципа суперпозиции и Леммы 3.
б) Пусть x(t) - какое-либо решение системы (1). Покажем, что оно имеет вид
(5). При каждом 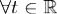 решение x(t) можно раздожить по жордановому
решение x(t) можно раздожить по жордановому
базису 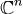 . Пусть
. Пусть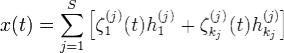
Подставим x(t) в (1) и воспользуемся определением жордановой цепочки. Имеем и из единственности разложениянаходим S систем вида:
решая эти системы приходи к утверждению теоремы.
28. Линейные обыкновенные дифференциальные уравнения с переменными коэффициентами.
Рассмотрим линейную неоднородную систему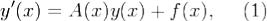 где
где  - заданная непрерывная на [α,β] квадратная матрица
- заданная непрерывная на [α,β] квадратная матрица
порядка n, f(x) - заданная непрерывная на [α,β] вектор-функция
с n компонентами.Непосредственно проверяется следующее предложение, называемое принципом суперпозиции для системы (1).
Лемма. Если 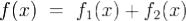 , y1(x) - решение системы (1) при условии
, y1(x) - решение системы (1) при условии  иy2(x) - решение системы (1) при усоловии
иy2(x) - решение системы (1) при усоловии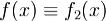 , то y(x) = y1(x) + y2(x) - решение системы (1).Если известно какое-либо частное решение (1), то интегрирование линейной неоднородной системы
, то y(x) = y1(x) + y2(x) - решение системы (1).Если известно какое-либо частное решение (1), то интегрирование линейной неоднородной системы
(1) сводится к интегрированию соответствующей (1) линейной однородной системы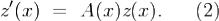
Теорема 1. Пусть y0(x) - некоторое частное решение (1), и Φ(x) - фундаментальная матрица (2). Тогда все решение системы (1) задаются формулой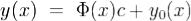 ,где c - произвольный n-мерный вектор. Доказательство. В системе (1) сделаем замену
,где c - произвольный n-мерный вектор. Доказательство. В системе (1) сделаем замену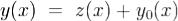 . Тогда получаем, что z(x) удовлетворяет системе (2). Общее решение системы (2), как установлено в 2, имеет вид
. Тогда получаем, что z(x) удовлетворяет системе (2). Общее решение системы (2), как установлено в 2, имеет вид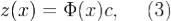
где c - произвольный числовой n-мерный вектор. Из замены следует утверждение теоремы.
Теорема 2. Если Φ(x) - фундоментальная матрица линейной однородной системы (2), то общее решение линейной неоднородной системы (1) при
всех 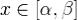 задается формулой
задается формулой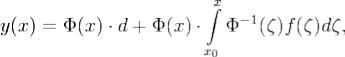 где
где 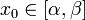 и d - произвольный числовой n - мерный вектор.
и d - произвольный числовой n - мерный вектор.
Доказательство. Согласно Лагранжу ищем решение (1) в таком же виде (3), что и решение однородной системы (2), но считаем c не постоянным, а непрерывно дифференцируемым вектором c(x), 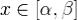 :
: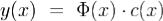
При таком переходе от y(x) к c(x) потери решений (1) не происходит, так как 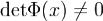 . Ниже будет видно, что такая замена неоднозначна. Функцию c(x) находим подстановкой y(x) в систему (1). Используя формулу производной произведения матрицы и вектор-функции, получаем, что
. Ниже будет видно, что такая замена неоднозначна. Функцию c(x) находим подстановкой y(x) в систему (1). Используя формулу производной произведения матрицы и вектор-функции, получаем, что
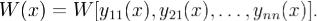
Φ'(x)c(x) + Φ(x)c'(x) = A(x)Φ(x)c(x) + f(x). Поскольку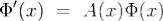 ,то
,то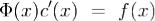 .
.
Так как матрица Φ(x) невырожденная на [α,β], то отсюда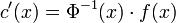 Это уравнение можно интегрировать, поскольку
Это уравнение можно интегрировать, поскольку 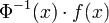 - непрерывная вектор-функция на [α,β]. Проинтегрировав последнее уравнение, получаем утверждение теоремы.
- непрерывная вектор-функция на [α,β]. Проинтегрировав последнее уравнение, получаем утверждение теоремы.
Фундаментальная система решений.
Определение. Матрица Φ(x) у которой столбцы образуют фундаметальную систему решений (1)  называется фундоментальной матрицей системы (1).
называется фундоментальной матрицей системы (1).
Таким образом,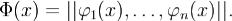
Очевидно, что Φ(x) - непрерывно дифференцируемая матрица на [α,β]. Из теоремы 2 следует, что для (1) существует бесконечно много фундометальных матриц. Из определения фундоментальной системы решений получаем, что Φ(x) - невырожденная матрица на [α,β]. Из теоремы 3 получаем самое важное свойство Φ(x). Именно, если Φ(x) - фундоментальная матрица (1), то общее решение системы (1) записывается в простом виде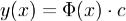 ,где c-произв числовой n-мерный вектор.
,где c-произв числовой n-мерный вектор.
Определитель Вронского. Формула Лиувилля-Остроградского.
Пусть  - система вектор-функций с n компонентами на [α,β]. Определение. Определителем Вронского системы
- система вектор-функций с n компонентами на [α,β]. Определение. Определителем Вронского системы наз.
наз.  .
.
Теорема. Пусть W(x) - вронскиан решений  системы (1) и пусть
системы (1) и пусть 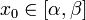 . Тогда для
. Тогда для 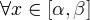 имеет место формула Лиувилля-
имеет место формула Лиувилля-
Остроградского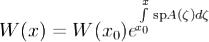 ,где
,где 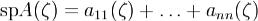 называется следом матрицы A(ζ).
называется следом матрицы A(ζ).
Доказательство. Покажем, что W(x) удовлетворяет дифференциальному уравнению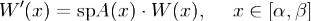 .
.
Пусть 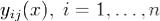 компоненты решения
компоненты решения 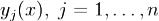 . Тогда W(x) является функцией всех этих компонент:
. Тогда W(x) является функцией всех этих компонент:
По формуле производной сложной функции получаем, что
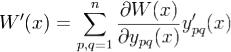 .Если Wpr(x) - алгебраическое дополнение ypr(x) в W(x), то разложение W(x) по p-й строке дает
.Если Wpr(x) - алгебраическое дополнение ypr(x) в W(x), то разложение W(x) по p-й строке дает
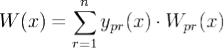 .Отсюда находим, что
.Отсюда находим, что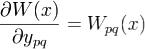 . Каждая вектор-функция yq(x) удовлетворяет системе (1), т.е.
. Каждая вектор-функция yq(x) удовлетворяет системе (1), т.е. 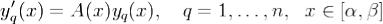 .Отсюда находим, что
.Отсюда находим, что
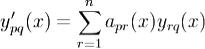 ,где apr(x) - элементы матрицы A(x). Подставляя найденные выражения
,где apr(x) - элементы матрицы A(x). Подставляя найденные выражения 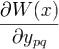 и y'pq(x) в формулу W'(x), получаем, что
и y'pq(x) в формулу W'(x), получаем, что
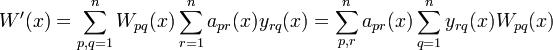 .
.
Но из курса алгебры известно, что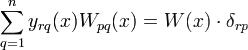 , где δrp - символ Кронекера. Тогда
, где δrp - символ Кронекера. Тогда
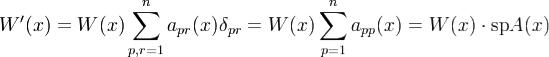 .
.
Интегрирование этого линейного однородного уравнения первого порядка и дает требуемую формулу (6).
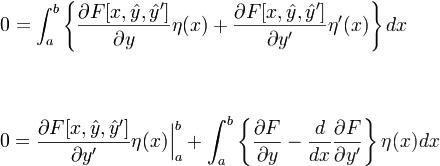
29.Простейшая задача вариационного исчисления. Уравнение Эйлера.
Обозначим через 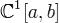 множество всех непрерывно дифференцируемых функций, заданных на [a,b]. Для
множество всех непрерывно дифференцируемых функций, заданных на [a,b]. Для 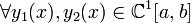 введем расстояние
введем расстояние
между ними 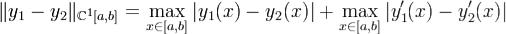 Множество функций C1[a,b] с введенной метрикой является линейным нормированным пространством.
Множество функций C1[a,b] с введенной метрикой является линейным нормированным пространством.
Пусть F(x,y,p) - заданная непрерывно дифференцируемая функция
для 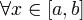 и
и 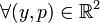 . Рассмотрим
. Рассмотрим 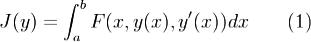 на множестве M тех функций
на множестве M тех функций 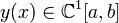 , которые удовлетворяют граничным условиям
, которые удовлетворяют граничным условиям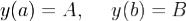 ,где A и B заданные числа. Функции
,где A и B заданные числа. Функции 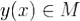 будем называть допустимыми.
будем называть допустимыми.
Определение. Говорят, что функция 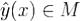 дает слабый локальный минимум функционала (1), если
дает слабый локальный минимум функционала (1), если 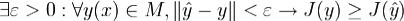 .
.
Определение. Задача нахождения слабого локального экстремума функционала (1) называетсяпростейшей вариационной задачей.
Теорема. Пусть функция F(x,y,p) - дважды непрерывно дифференцируема при 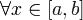 и
и 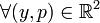 . Если дважды непрерывно дифференцируемая функция
. Если дважды непрерывно дифференцируемая функция 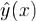 явл. решением простейшей вариационной задачи, то необх,
явл. решением простейшей вариационной задачи, то необх,
чтобы ф-ия 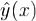 на [a,b] удовлетворяла ур-ию Эйлера
на [a,b] удовлетворяла ур-ию Эйлера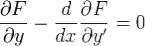 Доказательство. Условие экстремальности
Доказательство. Условие экстремальности
если второй интеграл взять по частям то приходим к следующему эквивалентному уравнению
ну и получаем утверждение теоремы.

33. Дифф-сть ф-ии комплексного переменного. Условия Коши-Римана. Определение. Говорят, что функция 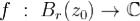 дифференцируема в точке
дифференцируема в точке 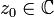 , если справедливо представление
, если справедливо представление
где A не зависит от Δz, а функция α(Δz) является o(Δz).
Лемма 1. Функция 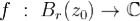 дифференцируема в точке z0 тогда и только тогда, когда существует производная
дифференцируема в точке z0 тогда и только тогда, когда существует производная 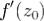 , причем в формуле число
, причем в формуле число 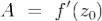 .
.
Доказательство. Распишем определение 1 через действительные и мнимые компоненты чисел и получим утверждение леммы 1. Теорема 1. Для того, чтобы функция 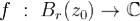 была дифференцируема в точке
была дифференцируема в точке 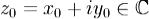 , н. и д., чтобы
, н. и д., чтобы
1)функция u(x,y) и v(x,y) были дифференцируемы в точке 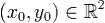 .
.
2)в точке (x0,y0) были выполнены условия Коши-Римана
При этом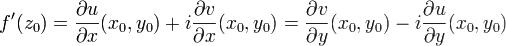 Доказательство. Пусть существует производная f'(z0), т.е. справедливы
Доказательство. Пусть существует производная f'(z0), т.е. справедливы
выражения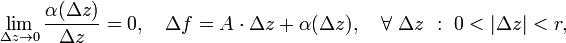 где
где 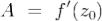 .Обозначим
.Обозначим 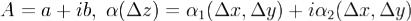 и распишем (5) через равенства действительных и мнимых частей, т.е.
и распишем (5) через равенства действительных и мнимых частей, т.е.
Δu = aΔx − bΔy + α1(Δx,Δy),Δv = bΔx + aΔy + α2(Δx,Δy), Из выражения (4) и того, что 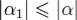 и
и 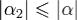 , т.е.
, т.е.
Откуда равенства (8) означают дифференцируемость по определению функции u(x,y) и v(x,y) в точке 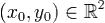 , причем
, причем
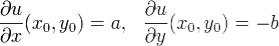 ,
, 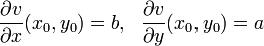
убеждаемся в выполнении условий Коши-Римана. Достаточность. Пусть функции u(x0,y0),v(x0,y0) дифференцируемы в точке (x0,y0) и выполнены условия Коши - Римана.
