Vse_bomby_s_dokazatelstvami

Доказательство. Для функции f(x) справедлива фломула НьютонаЛейбница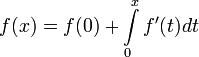.Так как производная 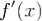абсолютно

интегрируемая функция, то существует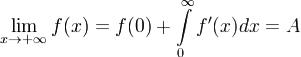. Покажем, что A = 0. Если, например,A > 0, то существует такое число ,

что при x > a выполнено неравенство 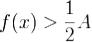, откуда по признаку

сравнения следует, что интеграл 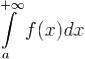является расходящимся, что противоречит условию теоремы. Итак, .

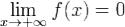Аналогично, доказывается, что .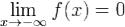

Применяя интегрирование по частям, получаем равенство

.

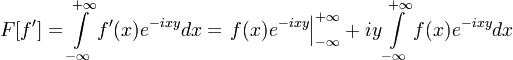Так как | e − ixy | = 1, то внеинтегральный член в правой части этого равенства обращается в нуль и, следовательно, справедливо равенство (6). Если функция f(x) непрерывна на 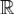, а функции f(x) и xf(x) абсолютно интегрируемы на 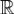, то функция 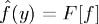имеет на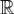

непрерывнуюпроизвудную, причем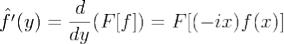. Доказательство. Дифференцируя интеграл (3) по параметру y, получаем

равенство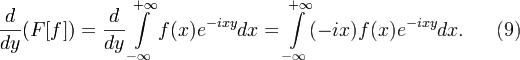 Обоснование законности дифференцирования под знаком интеграла сводится к проверке условий теоремы 6, 72.

Интеграл 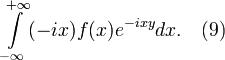сходится равномерно по пораметру y на 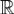по признаку Вейерштрасса, так

как 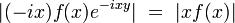, а интеграл 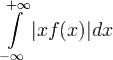сходится.

20. Углы между прямыми и плоскостями.Чтобы найти угол между двумя прямыми, следует найти их напрвляющие векторы и вычислить косинус угла между ними, используя скалярное произведение.

Для нахождения угла между прямой и плоскостью определяют угол θ между направляющим вектором прямой и нормальным вектором

плоскости. Если векторы выбрать так, чтобы 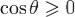, и взять 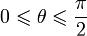, то искомый угол дополняет θ до π / 2.

Угол между плоскостями находят как угол между их нормальными векторами.Для двух прямых на плоскости{ y = k1x + b1, y = k2x + b2 }

Получаем для угла между прямыми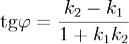,если знаменатель зануляется, то получаем, что прямые взаимно перпендикулярны.

Расстояния от точки до прямой и плоскости, между прямыми в пр-ве. Расстояние от точки до плоскости.

Пусть дана плоскость с уравнением 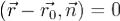и точка M с радиусвектором R. Рассмотрим вектор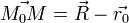, соединяющий начальную точку плоскости с M. Расстояние от точки до плоскости равно модулю его

скалярной проекции на вектор 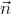, т.е.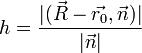.Если в декартовой прямоугольной системе кооррдинат точка M имеет координаты (X,Y,Z), то

равенство перепишеться в виде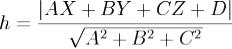

Расстояние от точки до прямой.

Если прямая задана уравнением 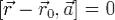, то мы можем найти расстояние h от точки M с радиус вектором 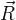, до этой прямой, разделив площадь параллелограмма, построенного на векторах 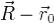и 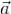, на длину

его основания. Результат можно записать в виде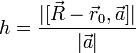

Рассмотрим прямую на плоскости, тогда получаем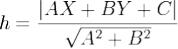

Расстояние между скрещивающимися прямыми.

Пусть прямые p и q не параллельны. Известно, что в этом случае существуют такие параллельные плоскости P и Q, что прямая p лежит в P, а

прямая q в Q. Расстояние h между P и Q называется расстоянием между прямыми p и q. Если p и q пересекаются, то P и Q совпадают и h = 0. Для того чтобы найти расстояние h, проще всего разделить объем

параллелепипеда, построенного на векторах 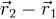, 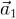и 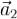, на площадь его основания. Мы получим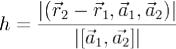

21. Общее решение системы линейных алгебраических уравнений. Теорема. Если 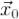- некоторое решение системы,

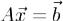а F - фундаментальная матрица её приведенной системы, то столбец 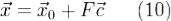при любом 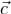является решением системы (1). Наоборот, для каждого её решения 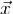найдется такой столбец 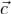, что оно будет представлено формулой (10).Выражение, стоящее в правой части формулы (10), называется общим решением системы линейных уравнений.

Если 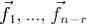- фундаментальная система решений, а c1,...,cn − r - произвольные постоянные, то формула (10) может быть написана так: .

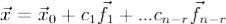Это теорема верна, в частности, и для однородных систем, если 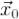- тривиальное решение.

Теорема Кронекера-Капелли.

Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Иначе утверждение теоремы можно сформулировать так: приписывание к матрице A размеров 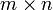стобца 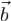высоты m не меняет её ранга тогда и только тогда, когда этот столбец - линейная комбинация столбцов A. Доказательство. Докажем это. Если RgA * = RgA, то базисный

минор A является базисным и для A * . Следовательно, 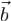раскладывается по базисным столбцам A. Мы можем считать его линейной комбинацией всех столбцов A, добавив недостающие столбцы с нулевыми коэффициентами. Обратно, если 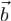раскладывается по столбцам A, то элементарными преобразованиями стобцов можно превратить A * в матрицу A0, получаемую из A приписыванием нулевого столбца.

Элементарно RgA0 = RgA * . C другой стороны, RgA0 = RgA, так как добавление нулевого столбца не может создать новых невырожденных подматриц. Отсюда RgA = RgA * , как и требовалось.

22. Линейное отображ конечномерных лин пространств, его матрица. Определение. Пусть 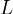и 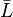- два линейных пространства, оба вещественные или оба комплексные. Под отображением A пространства 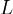в пространство 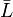понимается закон, по которому каждому вектору

из Lсопоставлен единственный вектор из 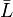. Мы будем писать 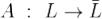. Образ вектора x обозначаетсяA(x)

Определение. Отображение 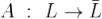называется линейным, если для любых векторов x и y из L и любого числа α выполнены равенства .

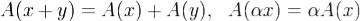Определение. Матрицей линейного отображения 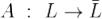в паре базисов e и f называется матрица, столбцы которой (в их естественнм порядке) - координатные столбцы векторов A(e1),...,A(en) в базисе f.

Теорема. При линейном отображение 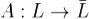линейное подпространство 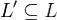переходит в линейное подпространство 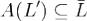, причем .

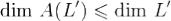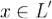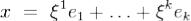Доказательство. Для нулевого подпространства доказательство очевидно. Рассмотрим подпространство L'размерности k > 0. Пусть - базис в L'. Для любого вектора имеем и .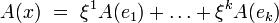

Определение. Ядро отображения - множество всех векторов переходящих в нулевой вектор при отображении.

Теорема. Ядро есть линейное подпространство.

Определение. Отображение при котором различные вектора имеют различные образы называется инъективным.

Теорема. Отображение инъективно тогда и только тогда, когда ядро есть нулевое подпространство.

Св-а собств векторов и собственных значений линейных преобразований. Линейное преобразование - это отображение, которое отображает линейное пространство в то же самое протстранство.

Определение. Если для числа λ подпространство Ker(A − λE) ненулевое, то λ называется собственным значением преобразования, а подпространство - собственным подпространством, соответствующим собственному значению λ.

Определение. Вектор x называется собственным вектором преобр-я A, соответствующим собственному значению λ, если: 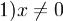; 2)A(x) = λx. Предположение 5. Собственные вектора и только они являются базисными векторами одномерных подпространств, инвариантных относительно A. Доказательство. Пусть вектор x собственный, а y принадлежит одномерному подпространству L' с базисомx. Тогда y = αx и A(y) = αA(x) = αλx. Значит, A(y) лежит в L'.

Пусть x - базис инвариантного подпространства L'. Тогда A(x) лежит в L' и раскладывается по базису: A(x) = λx. Так как 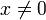, он собственный. Предположение 6. В i-м столбце матрицы линейного преобразования все элементы вне главной диагонали равны нулю тогда и только тогда, когда i- й базисный вектор собственный. В этом случае диагональный элемент столбца - собственное значение.

23. Самосопряженные преобразования евклидовых пространств, свойства их собственных значений и собственных векторов.

Линейное преобразование A евклидова пространства называется самосопряженным, если A = A * . Это равносильно тому, что (A(x),y) = (x,A(y)) для любых x и y.

Теорема 1. Все корни характеристического многочлена самосопряженного преобразования вещественны.

Доказательство. Допустим, что самосопряженное преобразование A имеет не вещественный корень характеристического многочлена. Тогда согласно предположению 8 4 гл. VI существует двумерное инвариантное подпространство Ε', не содержащее собственных векторов A. Обозначим через A'ограничение A на Ε'. Поскольку A' - самосопряженное преобразование, в ортонормированном базисе оно будет иметь

симметричную матрицу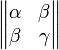 Характеристический многочлен этой матрицы λ2 − (α + γ)λ + (αγ − β2) имеет

дискриминант (α + γ)2 − 4(αγ − β2). Последнее легко преобразуется в (α − γ)2 + 4β2. Следовательно, дискриминант неотрицателен, характеристический многочлен имеет вещественный корень, а преобразование A' - собственный вектор, что противоречит выбору подпространства Ε'. Теорема доказана.

Теорема 2. Собственные подпространства самосопряженного преобразования попарно ортогональны.

Теорема равносильна следующему утверждению.

Если собственные векторы самосопряженного преобразования принадлежит различным собственным значениям, то они ортогональны. Доказательство. Пусть A(x) = λx и A(y) = μy, причем 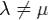. Тогда

(A(x),y) = λ(x,y).Но иначе можно получить

(A(x),y) = (x,A(y)) = μ(x,y).Из этих двух равенств следует (λ − μ)(x,y) = 0, откуда 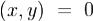, как и требовалось.

Теорема 3. Если подпространство 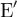инвариантно относительно самосопряженного преобразования A, то ортогональное дополнение 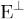этого подпространства - также инвариантно относительно A.

Доказательство. Нам дано, что для каждого x из 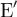образ A(x) также лежит в 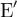. Поэтому (A(x),y) = 0 для любого 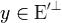. Но для

самосопряженного A это равносильно (x,A(y)) = 0, и, следовательно, 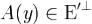, как и требовалось.

Теорема 4. Пусть A - самосопряженное преобразование евклидова пространства Ε. Тогда в Ε существует ортонормированный базис из собственных векторов A.

Доказательство. Обозначим через L сумму собственных подпространств преобразования A и докажем, что она совпадает с Ε. Сумма собственных подпространств - инвариантное подпространство. Действительно, если вектор x раскладывается в линейную комбинацию собственных векторов (принадлежащим каким бы то ни было собственным значениям), то его образ раскладывается по ним же.

Из теоремы 3 следует, что ортогональное дополнение L также инвариантно. Допустим, что подпространство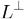ненулевое и рассмотрим ограничение A' преобразования A на 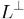. Это самосопряженное преобразование, и потому оно имеет вещественные характеристические числа и, следовательно, хоть один собственный вектор. Этот вектор собственный и для A и должен лежать в L. Так как он не нулевой, в 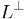он лежать не может. Полученное противоречие показывает, что 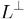- нулевое подпространство, и L совпадает с Ε.

24. Приведение квадратичных форм в линейном пространстве к каноническому виду.

Определение. Квадратичной формой или квадратичной функцией на линейном пространстве L называется функция k, значение которой на любом векторе x определяется равенством k(x) = b(x,x), где b - симметричная билинейная функция .

Определение. Матрицей квадратичной формы называется матрица соответствующей билинейной функции.

Мы имеем следующее выражение значения квадратичной формы через координатный столбец вектора: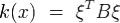

Теорема 1. Для каждой квадратичной формы k существует базис, в котром она имеет диагональный вид.

Доказательство. Пусть B - матрица квадратичной формы k в каком-либо базисе. Применим к матрице Bпоследовательность элементарных преобразований, которую для удобства описания разобьем на ряд шагов. На первом шаге возможны два случая.

1) Основной случай: β11. Если это так, вычистаем первую строку, умноженную на подходящие множители (β1i / β11 для i-й строки), из всех лежащих ниже строк и вычитаем первый столбец, умноженный на те же множители, из всех столбцов правее него. В результате матрица B перейдет

в матрицу B1 вида ,

где C1 - симметричная матрица порядка n − 1,

2) Особый случай: β1i = 0. Здесь имеются две возможности.

a) β1i = 0 для всех 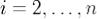. При этом матрица уже имеет нужный вид. б) Найдется i, для которого 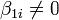. При этом делается вспомогательное преобразование: если 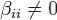, то i-я строка переставляется с первой, и i-й столбец переставляется с первым; если же βii = 0, то i-я строка прибавляется к первой и i-й столбец прибавляется к первому. В преобразованной матрице оказывается 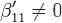. После вспомогательного преобразования матрица приводится к виду (10) так же, как и в основном случае.Пусть в результате k шагов мы получили матрицу

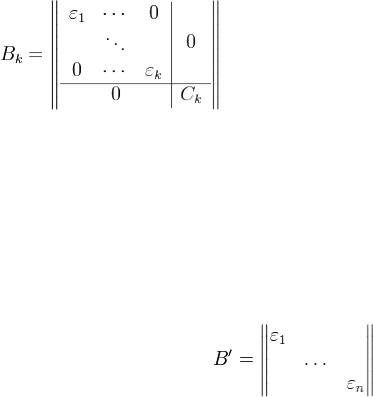
Здесь Ck - симметричная матрица порядка n − k. Следующий, (k + 1) - й шаг состоит в такой элементарной

последовательности преобразований последних n− k столбцов матрицы Bk, которая равносильна применению первого шага к матрице Ck. В результате мы получаем матрицу Bk + 1, имеющую тот же вид с большим

на 1 значением k. После (n − 1) - го шага матрицаCn − 1 имеет порядка 1 и не нуждается в преобразовании. В результате матрица B будет превращена в

диагональную матрицу