
- •Contents
- •Symbols and Abbreviations
- •Symbols
- •Greek Symbols
- •Subscripts
- •Abbreviations
- •Preface
- •Road Map of the Book
- •The Arrangement
- •Suggested Route for the Coursework
- •First Semester
- •Second Semester
- •Suggestions for the Class
- •Use of Semi-empirical Relations
- •1 Introduction
- •1.1 Overview
- •1.1.1 What Is to Be Learned?
- •1.1.2 Coursework Content
- •1.2 Brief Historical Background
- •1.3 Current Aircraft Design Status
- •1.3.1 Forces and Drivers
- •1.3.2 Current Civil Aircraft Design Trends
- •1.3.3 Current Military Aircraft Design Trends
- •1.4 Future Trends
- •1.4.1 Civil Aircraft Design: Future Trends
- •1.4.2 Military Aircraft Design: Future Trends
- •1.5 Learning Process
- •1.6 Units and Dimensions
- •1.7 Cost Implications
- •2 Methodology to Aircraft Design, Market Survey, and Airworthiness
- •2.1 Overview
- •2.1.1 What Is to Be Learned?
- •2.1.2 Coursework Content
- •2.2 Introduction
- •2.3 Typical Design Process
- •2.3.1 Four Phases of Aircraft Design
- •2.3.2 Typical Resources Deployment
- •2.3.3 Typical Cost Frame
- •2.3.4 Typical Time Frame
- •2.4 Typical Task Breakdown in Each Phase
- •Phase 1: Conceptual Study Phase (Feasibility Study)
- •Phase 3: Detailed Design Phase (Full-Scale Product Development)
- •2.4.1 Functional Tasks during the Conceptual Study (Phase 1: Civil Aircraft)
- •2.4.2 Project Activities for Small Aircraft Design
- •Phase 1: Conceptual Design (6 Months)
- •Phase 3: Detailed Design (Product Development) (12 Months)
- •2.5 Aircraft Familiarization
- •Fuselage Group
- •Wing Group
- •Empennage Group
- •Nacelle Group
- •Undercarriage Group
- •2.6 Market Survey
- •2.7 Civil Aircraft Market
- •2.8 Military Market
- •2.9 Comparison between Civil and Military Aircraft Design Requirements
- •2.10 Airworthiness Requirements
- •2.11 Coursework Procedures
- •3 Aerodynamic Considerations
- •3.1 Overview
- •3.1.1 What Is to Be Learned?
- •3.1.2 Coursework Content
- •3.2 Introduction
- •3.3 Atmosphere
- •3.4 Fundamental Equations
- •3.5.1 Flow Past Aerofoil
- •3.6 Aircraft Motion and Forces
- •3.6.1 Motion
- •3.6.2 Forces
- •3.7 Aerofoil
- •3.7.1 Groupings of Aerofoils and Their Properties
- •NACA Four-Digit Aerofoil
- •NACA Five-Digit Aerofoil
- •NACA Six-Digit Aerofoil
- •Other Types of Aerofoils
- •3.9 Generation of Lift
- •3.10 Types of Stall
- •3.10.1 Gradual Stall
- •3.10.2 Abrupt Stall
- •3.11 Comparison of Three NACA Aerofoils
- •3.12 High-Lift Devices
- •3.13 Transonic Effects – Area Rule
- •3.14 Wing Aerodynamics
- •3.14.1 Induced Drag and Total Aircraft Drag
- •3.15 Aspect Ratio Correction of 2D Aerofoil Characteristics for 3D Finite Wing
- •3.16.1 Planform Area, SW
- •3.16.2 Wing Aspect Ratio
- •3.16.4 Wing Root (Croot) and Tip (Ctip) Chord
- •3.16.6 Wing Twist
- •3.17 Mean Aerodynamic Chord
- •3.18 Compressibility Effect: Wing Sweep
- •3.19 Wing Stall Pattern and Wing Twist
- •3.20.1 The Square-Cube Law
- •3.20.2 Aircraft Wetted Area (AW) versus Wing Planform Area (Sw)
- •3.20.3 Additional Vortex Lift
- •3.20.4 Additional Surfaces on Wing
- •3.21 Finalizing Wing Design Parameters
- •3.22 Empennage
- •3.22.1 H-Tail
- •3.22.2 V-Tail
- •3.23 Fuselage
- •3.23.2 Fuselage Length, Lfus
- •3.23.3 Fineness Ratio, FR
- •3.23.4 Fuselage Upsweep Angle
- •3.23.5 Fuselage Closure Angle
- •3.23.6 Front Fuselage Closure Length, Lf
- •3.23.7 Aft Fuselage Closure Length, La
- •3.23.8 Midfuselage Constant Cross-Section Length, Lm
- •3.23.9 Fuselage Height, H
- •3.23.10 Fuselage Width, W
- •3.23.11 Average Diameter, Dave
- •3.23.12 Cabin Height, Hcab
- •3.23.13 Cabin Width, Wcab
- •3.24 Undercarriage
- •3.25 Nacelle and Intake
- •3.26 Speed Brakes and Dive Brakes
- •4.1 Overview
- •4.1.1 What Is to Be Learned?
- •4.1.2 Coursework Content
- •4.2 Introduction
- •4.3 Aircraft Evolution
- •4.4 Civil Aircraft Mission (Payload-Range)
- •4.5 Civil Subsonic Jet Aircraft Statistics (Sizing Parameters and Regression Analysis)
- •4.5.1 Maximum Takeoff Mass versus Number of Passengers
- •4.5.2 Maximum Takeoff Mass versus Operational Empty Mass
- •4.5.3 Maximum Takeoff Mass versus Fuel Load
- •4.5.4 Maximum Takeoff Mass versus Wing Area
- •4.5.5 Maximum Takeoff Mass versus Engine Power
- •4.5.6 Empennage Area versus Wing Area
- •4.5.7 Wing Loading versus Aircraft Span
- •4.6 Civil Aircraft Component Geometries
- •4.7 Fuselage Group
- •4.7.1 Fuselage Width
- •4.7.2 Fuselage Length
- •4.7.3 Front (Nose Cone) and Aft-End Closure
- •4.7.4 Flight Crew (Flight Deck) Compartment Layout
- •4.7.5 Cabin Crew and Passenger Facilities
- •4.7.6 Seat Arrangement, Pitch, and Posture (95th Percentile) Facilities
- •4.7.7 Passenger Facilities
- •4.7.8 Cargo Container Sizes
- •4.7.9 Doors – Emergency Exits
- •4.8 Wing Group
- •4.9 Empennage Group (Civil Aircraft)
- •4.10 Nacelle Group
- •4.11 Summary of Civil Aircraft Design Choices
- •4.13 Military Aircraft Mission
- •4.14.1 Military Aircraft Maximum Take-off Mass (MTOM) versus Payload
- •4.14.2 Military MTOM versus OEM
- •4.14.3 Military MTOM versus Fuel Load Mf
- •4.14.4 MTOM versus Wing Area (Military)
- •4.14.5 MTOM versus Engine Thrust (Military)
- •4.14.6 Empennage Area versus Wing Area (Military)
- •4.14.7 Aircraft Wetted Area versus Wing Area (Military)
- •4.15 Military Aircraft Component Geometries
- •4.16 Fuselage Group (Military)
- •4.17 Wing Group (Military)
- •4.17.1 Generic Wing Planform Shapes
- •4.18 Empennage Group (Military)
- •4.19 Intake/Nacelle Group (Military)
- •4.20 Undercarriage Group
- •4.21 Miscellaneous Comments
- •4.22 Summary of Military Aircraft Design Choices
- •5 Aircraft Load
- •5.1 Overview
- •5.1.1 What Is to Be Learned?
- •5.1.2 Coursework Content
- •5.2 Introduction
- •5.2.1 Buffet
- •5.2.2 Flutter
- •5.3 Flight Maneuvers
- •5.3.1 Pitch Plane (X-Z) Maneuver (Elevator/Canard-Induced)
- •5.3.2 Roll Plane (Y-Z) Maneuver (Aileron-Induced)
- •5.3.3 Yaw Plane (Z-X) Maneuver (Rudder-Induced)
- •5.4 Aircraft Loads
- •5.4.1 On the Ground
- •5.4.2 In Flight
- •5.5.1 Load Factor, n
- •5.6 Limits – Load and Speeds
- •5.6.1 Maximum Limit of Load Factor
- •5.6.2 Speed Limits
- •5.7 V-n Diagram
- •5.7.1 Low-Speed Limit
- •5.7.2 High-Speed Limit
- •5.7.3 Extreme Points of a V-n Diagram
- •Positive Loads
- •Negative Loads
- •5.8 Gust Envelope
- •6.1 Overview
- •6.1.1 What Is to Be Learned?
- •6.1.2 Coursework Content
- •6.2 Introduction
- •Closure of the Fuselage
- •6.4 Civil Aircraft Fuselage: Typical Shaping and Layout
- •6.4.1 Narrow-Body, Single-Aisle Aircraft
- •6.4.2 Wide-Body, Double-Aisle Aircraft
- •6.4.3 Worked-Out Example: Civil Aircraft Fuselage Layout
- •6.5.1 Aerofoil Selection
- •6.5.2 Wing Design
- •Planform Shape
- •Wing Reference Area
- •Wing Sweep
- •Wing Twist
- •Wing Dihedral/Anhedral
- •6.5.3 Wing-Mounted Control-Surface Layout
- •6.5.4 Positioning of the Wing Relative to the Fuselage
- •6.6.1 Horizontal Tail
- •6.6.2 Vertical Tail
- •6.8 Undercarriage Positioning
- •6.10 Miscellaneous Considerations in Civil Aircraft
- •6.12.1 Use of Statistics in the Class of Military Trainer Aircraft
- •6.12.3 Miscellaneous Considerations – Military Design
- •6.13 Variant CAS Design
- •6.13.1 Summary of the Worked-Out Military Aircraft Preliminary Details
- •7 Undercarriage
- •7.1 Overview
- •7.1.1 What Is to Be Learned?
- •7.1.2 Coursework Content
- •7.2 Introduction
- •7.3 Types of Undercarriage
- •7.5 Undercarriage Retraction and Stowage
- •7.5.1 Stowage Space Clearances
- •7.6 Undercarriage Design Drivers and Considerations
- •7.7 Turning of an Aircraft
- •7.8 Wheels
- •7.9 Loads on Wheels and Shock Absorbers
- •7.9.1 Load on Wheels
- •7.9.2 Energy Absorbed
- •7.11 Tires
- •7.13 Undercarriage Layout Methodology
- •7.14 Worked-Out Examples
- •7.14.1 Civil Aircraft: Bizjet
- •Baseline Aircraft with 10 Passengers at a 33-Inch Pitch
- •Shrunk Aircraft (Smallest in the Family Variant) with 6 Passengers at a 33-Inch Pitch
- •7.14.2 Military Aircraft: AJT
- •7.15 Miscellaneous Considerations
- •7.16 Undercarriage and Tire Data
- •8 Aircraft Weight and Center of Gravity Estimation
- •8.1 Overview
- •8.1.1 What Is to Be Learned?
- •8.1.2 Coursework Content
- •8.2 Introduction
- •8.3 The Weight Drivers
- •8.4 Aircraft Mass (Weight) Breakdown
- •8.5 Desirable CG Position
- •8.6 Aircraft Component Groups
- •8.6.1 Civil Aircraft
- •8.6.2 Military Aircraft (Combat Category)
- •8.7 Aircraft Component Mass Estimation
- •8.8 Rapid Mass Estimation Method: Civil Aircraft
- •8.9 Graphical Method for Predicting Aircraft Component Weight: Civil Aircraft
- •8.10 Semi-empirical Equation Method (Statistical)
- •8.10.1 Fuselage Group – Civil Aircraft
- •8.10.2 Wing Group – Civil Aircraft
- •8.10.3 Empennage Group – Civil Aircraft
- •8.10.4 Nacelle Group – Civil Aircraft
- •Jet Type (Includes Pylon Mass)
- •Turboprop Type
- •Piston-Engine Nacelle
- •8.10.5 Undercarriage Group – Civil Aircraft
- •Tricycle Type (Retractable) – Fuselage-Mounted (Nose and Main Gear Estimated Together)
- •8.10.6 Miscellaneous Group – Civil Aircraft
- •8.10.7 Power Plant Group – Civil Aircraft
- •Turbofans
- •Turboprops
- •Piston Engines
- •8.10.8 Systems Group – Civil Aircraft
- •8.10.9 Furnishing Group – Civil Aircraft
- •8.10.10 Contingency and Miscellaneous – Civil Aircraft
- •8.10.11 Crew – Civil Aircraft
- •8.10.12 Payload – Civil Aircraft
- •8.10.13 Fuel – Civil Aircraft
- •8.11 Worked-Out Example – Civil Aircraft
- •8.11.1 Fuselage Group Mass
- •8.11.2 Wing Group Mass
- •8.11.3 Empennage Group Mass
- •8.11.4 Nacelle Group Mass
- •8.11.5 Undercarriage Group Mass
- •8.11.6 Miscellaneous Group Mass
- •8.11.7 Power Plant Group Mass
- •8.11.8 Systems Group Mass
- •8.11.9 Furnishing Group Mass
- •8.11.10 Contingency Group Mass
- •8.11.11 Crew Mass
- •8.11.12 Payload Mass
- •8.11.13 Fuel Mass
- •8.11.14 Weight Summary
- •Variant Aircraft in the Family
- •8.12 Center of Gravity Determination
- •8.12.1 Bizjet Aircraft CG Location Example
- •8.12.2 First Iteration to Fine Tune CG Position Relative to Aircraft and Components
- •8.13 Rapid Mass Estimation Method – Military Aircraft
- •8.14 Graphical Method to Predict Aircraft Component Weight – Military Aircraft
- •8.15 Semi-empirical Equation Methods (Statistical) – Military Aircraft
- •8.15.1 Military Aircraft Fuselage Group (SI System)
- •8.15.2 Military Aircraft Wing Mass (SI System)
- •8.15.3 Military Aircraft Empennage
- •8.15.4 Nacelle Mass Example – Military Aircraft
- •8.15.5 Power Plant Group Mass Example – Military Aircraft
- •8.15.6 Undercarriage Mass Example – Military Aircraft
- •8.15.7 System Mass – Military Aircraft
- •8.15.8 Aircraft Furnishing – Military Aircraft
- •8.15.11 Crew Mass
- •8.16.1 AJT Fuselage Example (Based on CAS Variant)
- •8.16.2 AJT Wing Example (Based on CAS Variant)
- •8.16.3 AJT Empennage Example (Based on CAS Variant)
- •8.16.4 AJT Nacelle Mass Example (Based on CAS Variant)
- •8.16.5 AJT Power Plant Group Mass Example (Based on AJT Variant)
- •8.16.6 AJT Undercarriage Mass Example (Based on CAS Variant)
- •8.16.7 AJT Systems Group Mass Example (Based on AJT Variant)
- •8.16.8 AJT Furnishing Group Mass Example (Based on AJT Variant)
- •8.16.9 AJT Contingency Group Mass Example
- •8.16.10 AJT Crew Mass Example
- •8.16.13 Weights Summary – Military Aircraft
- •8.17 CG Position Determination – Military Aircraft
- •8.17.1 Classroom Worked-Out Military AJT CG Location Example
- •8.17.2 First Iteration to Fine Tune CG Position and Components Masses
- •9 Aircraft Drag
- •9.1 Overview
- •9.1.1 What Is to Be Learned?
- •9.1.2 Coursework Content
- •9.2 Introduction
- •9.4 Aircraft Drag Breakdown (Subsonic)
- •9.5 Aircraft Drag Formulation
- •9.6 Aircraft Drag Estimation Methodology (Subsonic)
- •9.7 Minimum Parasite Drag Estimation Methodology
- •9.7.2 Computation of Wetted Areas
- •Lifting Surfaces
- •Fuselage
- •Nacelle
- •9.7.3 Stepwise Approach to Compute Minimum Parasite Drag
- •9.8 Semi-empirical Relations to Estimate Aircraft Component Parasite Drag
- •9.8.1 Fuselage
- •9.8.2 Wing, Empennage, Pylons, and Winglets
- •9.8.3 Nacelle Drag
- •Intake Drag
- •Base Drag
- •Boat-Tail Drag
- •9.8.4 Excrescence Drag
- •9.8.5 Miscellaneous Parasite Drags
- •Air-Conditioning Drag
- •Trim Drag
- •Aerials
- •9.9 Notes on Excrescence Drag Resulting from Surface Imperfections
- •9.10 Minimum Parasite Drag
- •9.12 Subsonic Wave Drag
- •9.13 Total Aircraft Drag
- •9.14 Low-Speed Aircraft Drag at Takeoff and Landing
- •9.14.1 High-Lift Device Drag
- •9.14.2 Dive Brakes and Spoilers Drag
- •9.14.3 Undercarriage Drag
- •9.14.4 One-Engine Inoperative Drag
- •9.15 Propeller-Driven Aircraft Drag
- •9.16 Military Aircraft Drag
- •9.17 Supersonic Drag
- •9.18 Coursework Example: Civil Bizjet Aircraft
- •9.18.1 Geometric and Performance Data
- •Fuselage (see Figure 9.13)
- •Wing (see Figure 9.13)
- •Empennage (see Figure 9.13)
- •Nacelle (see Figure 9.13)
- •9.18.2 Computation of Wetted Areas, Re, and Basic CF
- •Fuselage
- •Wing
- •Empennage (same procedure as for the wing)
- •Nacelle
- •Pylon
- •9.18.3 Computation of 3D and Other Effects to Estimate Component
- •Fuselage
- •Wing
- •Empennage
- •Nacelle
- •Pylon
- •9.18.4 Summary of Parasite Drag
- •9.18.5 CDp Estimation
- •9.18.6 Induced Drag
- •9.18.7 Total Aircraft Drag at LRC
- •9.19 Coursework Example: Subsonic Military Aircraft
- •9.19.1 Geometric and Performance Data of a Vigilante RA-C5 Aircraft
- •Fuselage
- •Wing
- •Empennage
- •9.19.2 Computation of Wetted Areas, Re, and Basic CF
- •Fuselage
- •Wing
- •Empennage (same procedure as for the wing)
- •9.19.3 Computation of 3D and Other Effects to Estimate Component CDpmin
- •Fuselage
- •Wing
- •Empennage
- •9.19.4 Summary of Parasite Drag
- •9.19.5 CDp Estimation
- •9.19.6 Induced Drag
- •9.19.7 Supersonic Drag Estimation
- •9.19.8 Total Aircraft Drag
- •9.20 Concluding Remarks
- •10 Aircraft Power Plant and Integration
- •10.1 Overview
- •10.1.1 What Is to Be Learned?
- •10.1.2 Coursework Content
- •10.2 Background
- •10.4 Introduction: Air-Breathing Aircraft Engine Types
- •10.4.1 Simple Straight-Through Turbojet
- •10.4.2 Turbofan: Bypass Engine
- •10.4.3 Afterburner Engine
- •10.4.4 Turboprop Engine
- •10.4.5 Piston Engine
- •10.6 Formulation and Theory: Isentropic Case
- •10.6.1 Simple Straight-Through Turbojet Engine: Formulation
- •10.6.2 Bypass Turbofan Engine: Formulation
- •10.6.3 Afterburner Engine: Formulation
- •10.6.4 Turboprop Engine: Formulation
- •Summary
- •10.7 Engine Integration with an Aircraft: Installation Effects
- •10.7.1 Subsonic Civil Aircraft Nacelle and Engine Installation
- •10.7.2 Turboprop Integration to Aircraft
- •10.7.3 Combat Aircraft Engine Installation
- •10.8 Intake and Nozzle Design
- •10.8.1 Civil Aircraft Intake Design: Inlet Sizing
- •10.8.2 Military Aircraft Intake Design
- •10.9 Exhaust Nozzle and Thrust Reverser
- •10.9.1 Civil Aircraft Thrust Reverser Application
- •10.9.2 Civil Aircraft Exhaust Nozzles
- •10.9.3 Coursework Example of Civil Aircraft Nacelle Design
- •Intake Geometry (see Section 10.8.1)
- •Lip Section (Crown Cut)
- •Lip Section (Keel Cut)
- •Nozzle Geometry
- •10.9.4 Military Aircraft Thrust Reverser Application and Exhaust Nozzles
- •10.10 Propeller
- •10.10.2 Propeller Theory
- •Momentum Theory: Actuator Disc
- •Blade-Element Theory
- •10.10.3 Propeller Performance: Practical Engineering Applications
- •Static Performance (see Figures 10.34 and 10.36)
- •In-Flight Performance (see Figures 10.35 and 10.37)
- •10.10.5 Propeller Performance at STD Day: Worked-Out Example
- •10.11 Engine-Performance Data
- •Takeoff Rating
- •Maximum Continuous Rating
- •Maximum Climb Rating
- •Maximum Cruise Rating
- •Idle Rating
- •10.11.1 Piston Engine
- •10.11.2 Turboprop Engine (Up to 100 Passengers Class)
- •Takeoff Rating
- •Maximum Climb Rating
- •Maximum Cruise Rating
- •10.11.3 Turbofan Engine: Civil Aircraft
- •Turbofans with a BPR Around 4 (Smaller Engines; e.g., Bizjets)
- •Turbofans with a BPR around 5 or 7 (Larger Engines; e.g., RJs and Larger)
- •10.11.4 Turbofan Engine – Military Aircraft
- •11 Aircraft Sizing, Engine Matching, and Variant Derivative
- •11.1 Overview
- •11.1.1 What Is to Be Learned?
- •11.1.2 Coursework Content
- •11.2 Introduction
- •11.3 Theory
- •11.3.1 Sizing for Takeoff Field Length
- •Civil Aircraft Design: Takeoff
- •Military Aircraft Design: Takeoff
- •11.3.2 Sizing for the Initial Rate of Climb
- •11.3.3 Sizing to Meet Initial Cruise
- •11.3.4 Sizing for Landing Distance
- •11.4 Coursework Exercises: Civil Aircraft Design (Bizjet)
- •11.4.1 Takeoff
- •11.4.2 Initial Climb
- •11.4.3 Cruise
- •11.4.4 Landing
- •11.5 Coursework Exercises: Military Aircraft Design (AJT)
- •11.5.1 Takeoff – Military Aircraft
- •11.5.2 Initial Climb – Military Aircraft
- •11.5.3 Cruise – Military Aircraft
- •11.5.4 Landing – Military Aircraft
- •11.6 Sizing Analysis: Civil Aircraft (Bizjet)
- •11.6.1 Variants in the Family of Aircraft Design
- •11.6.2 Example: Civil Aircraft
- •11.7 Sizing Analysis: Military Aircraft
- •11.7.1 Single-Seat Variant in the Family of Aircraft Design
- •11.8 Sensitivity Study
- •11.9 Future Growth Potential
- •12.1 Overview
- •12.1.1 What Is to Be Learned?
- •12.1.2 Coursework Content
- •12.2 Introduction
- •12.3 Static and Dynamic Stability
- •12.3.1 Longitudinal Stability: Pitch Plane (Pitch Moment, M)
- •12.3.2 Directional Stability: Yaw Plane (Yaw Moment, N)
- •12.3.3 Lateral Stability: Roll Plane (Roll Moment, L)
- •12.3.4 Summary of Forces, Moments, and Their Sign Conventions
- •12.4 Theory
- •12.4.1 Pitch Plane
- •12.4.2 Yaw Plane
- •12.4.3 Roll Plane
- •12.6 Inherent Aircraft Motions as Characteristics of Design
- •12.6.1 Short-Period Oscillation and Phugoid Motion
- •12.6.2 Directional and Lateral Modes of Motion
- •12.7 Spinning
- •12.8 Design Considerations for Stability: Civil Aircraft
- •12.9 Military Aircraft: Nonlinear Effects
- •12.10 Active Control Technology: Fly-by-Wire
- •13 Aircraft Performance
- •13.1 Overview
- •13.1.1 What Is to Be Learned?
- •13.1.2 Coursework Content
- •13.2 Introduction
- •13.2.1 Aircraft Speed
- •13.3 Establish Engine Performance Data
- •13.3.1 Turbofan Engine (BPR < 4)
- •Takeoff Rating (Bizjet): Standard Day
- •Maximum Climb Rating (Bizjet): Standard Day
- •Maximum Cruise Rating (Bizjet): Standard Day
- •13.3.2 Turbofan Engine (BPR > 4)
- •13.3.3 Military Turbofan (Advanced Jet Trainer/CAS Role – Very Low BPR) – STD Day
- •13.3.4 Turboprop Engine Performance
- •Takeoff Rating (Turboprop): Standard Day
- •Maximum Climb Rating (Turboprop): Standard Day
- •Maximum Cruise Rating (Turboprop): Standard Day
- •13.4 Derivation of Pertinent Aircraft Performance Equations
- •13.4.1 Takeoff
- •Balanced Field Length: Civil Aircraft
- •Takeoff Equations
- •13.4.2 Landing Performance
- •13.4.3 Climb and Descent Performance
- •Summary
- •Descent
- •13.4.4 Initial Maximum Cruise Speed
- •13.4.5 Payload Range Capability
- •13.5 Aircraft Performance Substantiation: Worked-Out Examples (Bizjet)
- •13.5.1 Takeoff Field Length (Bizjet)
- •Segment A: All Engines Operating up to the Decision Speed V1
- •Segment B: One-Engine Inoperative Acceleration from V1 to Liftoff Speed, VLO
- •Segment C: Flaring Distance with One Engine Inoperative from VLO to V2
- •Segment E: Braking Distance from VB to Zero Velocity (Flap Settings Are of Minor Consequence)
- •Discussion of the Takeoff Analysis
- •13.5.2 Landing Field Length (Bizjet)
- •13.5.3 Climb Performance Requirements (Bizjet)
- •13.5.4 Integrated Climb Performance (Bizjet)
- •13.5.5 Initial High-Speed Cruise (Bizjet)
- •13.5.7 Descent Performance (Bizjet)
- •13.5.8 Payload Range Capability
- •13.6 Aircraft Performance Substantiation: Military Aircraft (AJT)
- •13.6.2 Takeoff Field Length (AJT)
- •Distance Covered from Zero to the Decision Speed V1
- •Distance Covered from Zero to Liftoff Speed VLO
- •Distance Covered from VLO to V2
- •Total Takeoff Distance
- •Stopping Distance and the CFL
- •Distance Covered from V1 to Braking Speed VB
- •Verifying the Climb Gradient at an 8-Deg Flap
- •13.6.3 Landing Field Length (AJT)
- •13.6.4 Climb Performance Requirements (AJT)
- •13.6.5 Maximum Speed Requirements (AJT)
- •13.6.6 Fuel Requirements (AJT)
- •13.7 Summary
- •13.7.1 The Bizjet
- •14 Computational Fluid Dynamics
- •14.1 Overview
- •14.1.1 What Is to Be Learned?
- •14.1.2 Coursework Content
- •14.2 Introduction
- •14.3 Current Status
- •14.4 Approach to CFD Analyses
- •14.4.1 In the Preprocessor (Menu-Driven)
- •14.4.2 In the Flow Solver (Menu-Driven)
- •14.4.3 In the Postprocessor (Menu-Driven)
- •14.5 Case Studies
- •14.6 Hierarchy of CFD Simulation Methods
- •14.6.1 DNS Simulation Technique
- •14.6.2 Large Eddy Simulation (LES) Technique
- •14.6.3 Detached Eddy Simulation (DES) Technique
- •14.6.4 RANS Equation Technique
- •14.6.5 Euler Method Technique
- •14.6.6 Full-Potential Flow Equations
- •14.6.7 Panel Method
- •14.7 Summary
- •15 Miscellaneous Design Considerations
- •15.1 Overview
- •15.1.1 What Is to Be Learned?
- •15.1.2 Coursework Content
- •15.2 Introduction
- •15.2.1 Environmental Issues
- •15.2.2 Materials and Structures
- •15.2.3 Safety Issues
- •15.2.4 Human Interface
- •15.2.5 Systems Architecture
- •15.2.6 Military Aircraft Survivability Issues
- •15.2.7 Emerging Scenarios
- •15.3 Noise Emissions
- •Approach
- •Sideline
- •15.3.1 Summary
- •15.4 Engine Exhaust Emissions
- •15.5 Aircraft Materials
- •15.5.1 Material Properties
- •15.5.2 Material Selection
- •15.5.3 Coursework Overview
- •Civil Aircraft Design
- •Military Aircraft Design
- •15.6 Aircraft Structural Considerations
- •15.7 Doors: Emergency Egress
- •Coursework Exercise
- •15.8 Aircraft Flight Deck (Cockpit) Layout
- •15.8.1 Multifunctional Display and Electronic Flight Information System
- •15.8.2 Combat Aircraft Flight Deck
- •15.8.3 Civil Aircraft Flight Deck
- •15.8.4 Head-Up Display
- •15.8.5 Helmet-Mounted Display
- •15.8.6 Hands-On Throttle and Stick
- •15.8.7 Voice-Operated Control
- •15.9 Aircraft Systems
- •15.9.1 Aircraft Control Subsystem
- •15.9.2 Engine and Fuel Control Subsystems
- •Piston Engine Fuel Control System (The total system weight is approximately 1 to 1.5% of the MTOW)
- •Turbofan Engine Fuel Control System (The total system weight is approximately 1.5 to 2% of the MTOW)
- •Fuel Storage and Flow Management
- •15.9.3 Emergency Power Supply
- •15.9.4 Avionics Subsystems
- •Military Aircraft Application
- •Civil Aircraft Application
- •15.9.5 Electrical Subsystem
- •15.9.6 Hydraulic Subsystem
- •15.9.7 Pneumatic System
- •ECS: Cabin Pressurization and Air-Conditioning
- •Oxygen Supply
- •Anti-icing, De-icing, Defogging, and Rain-Removal Systems
- •Defogging and Rain-Removal Systems
- •15.9.8 Utility Subsystem
- •15.9.9 End-of-Life Disposal
- •15.10 Military Aircraft Survivability
- •15.10.1 Military Emergency Escape
- •15.10.2 Military Aircraft Stealth Consideration
- •15.11 Emerging Scenarios
- •Counterterrorism Design Implementation
- •Health Issues
- •Damage from Runway Debris
- •16 Aircraft Cost Considerations
- •16.1 Overview
- •16.1.1 What Is to Be Learned?
- •16.1.2 Coursework Content
- •16.2 Introduction
- •16.3 Aircraft Cost and Operational Cost
- •Operating Cost
- •16.4 Aircraft Costing Methodology: Rapid-Cost Model
- •16.4.1 Nacelle Cost Drivers
- •Group 1
- •Group 2
- •16.4.2 Nose Cowl Parts and Subassemblies
- •16.4.3 Methodology (Nose Cowl Only)
- •Cost of Parts Fabrication
- •Subassemblies
- •Cost of Amortization of the NRCs
- •16.4.4 Cost Formulas and Results
- •16.5 Aircraft Direct Operating Cost
- •16.5.1 Formulation to Estimate DOC
- •Aircraft Price
- •Fixed-Cost Elements
- •Trip-Cost Elements
- •16.5.2 Worked-Out Example of DOC: Bizjet
- •Aircraft Price
- •Fixed-Cost Elements
- •Trip-Cost Elements
- •OC of the Variants in the Family
- •17 Aircraft Manufacturing Considerations
- •17.1 Overview
- •17.1.1 What Is to Be Learned?
- •17.1.2 Coursework Content
- •17.2 Introduction
- •17.3 Design for Manufacture and Assembly
- •17.4 Manufacturing Practices
- •17.5 Six Sigma Concept
- •17.6 Tolerance Relaxation at the Wetted Surface
- •17.6.1 Sources of Aircraft Surface Degeneration
- •17.6.2 Cost-versus-Tolerance Relationship
- •17.7 Reliability and Maintainability
- •17.8 Design Considerations
- •17.8.1 Category I: Technology-Driven Design Considerations
- •17.8.2 Category II: Manufacture-Driven Design Considerations
- •17.8.3 Category III: Management-Driven Design Considerations
- •17.8.4 Category IV: Operator-Driven Design Considerations
- •17.9 “Design for Customer”
- •17.9.1 Index for “Design for Customer”
- •17.9.2 Worked-Out Example
- •Standard Parameters of the Baseline Aircraft
- •Parameters of the Extended Variant Aircraft
- •Parameters of the Shortened Variant Aircraft
- •17.10 Digital Manufacturing Process Management
- •Process Detailing and Validation
- •Resource Modeling and Simulation
- •Process Planning and Simulation
- •17.10.1 Product, Process, and Resource Hub
- •17.10.3 Shop-Floor Interface
- •17.10.4 Design for Maintainability and 3D-Based Technical Publication Generation
- •Midrange Aircraft (Airbus 320 class)
- •References
- •ROAD MAP OF THE BOOK
- •CHAPTER 1. INTRODUCTION
- •CHAPTER 3. AERODYNAMIC CONSIDERATIONS
- •CHAPTER 5. AIRCRAFT LOAD
- •CHAPTER 6. CONFIGURING AIRCRAFT
- •CHAPTER 7. UNDERCARRIAGE
- •CHAPTER 8. AIRCRAFT WEIGHT AND CENTER OF GRAVITY ESTIMATION
- •CHAPTER 9. AIRCRAFT DRAG
- •CHAPTER 10. AIRCRAFT POWER PLANT AND INTEGRATION
- •CHAPTER 11. AIRCRAFT SIZING, ENGINE MATCHING, AND VARIANT DERIVATIVE
- •CHAPTER 12. STABILITY CONSIDERATIONS AFFECTING AIRCRAFT CONFIGURATION
- •CHAPTER 13. AIRCRAFT PERFORMANCE
- •CHAPTER 14. COMPUTATIONAL FLUID DYNAMICS
- •CHAPTER 15. MISCELLANEOUS DESIGN CONSIDERATIONS
- •CHAPTER 16. AIRCRAFT COST CONSIDERATIONS
- •CHAPTER 17. AIRCRAFT MANUFACTURING CONSIDERATIONS
- •Index
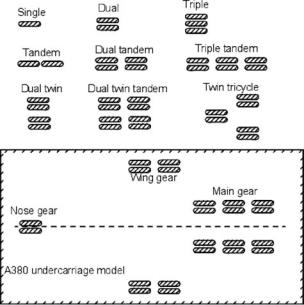
202 |
Undercarriage |
Figure 7.11. Wheel arrangements
7.8 Wheels
As an aircraft weight increases, the runway must bear the reaction and retain integrity to keep the vehicle’s field performance safe. Heavy commercial transport aircraft are intended to operate from a prepared runway (i.e., Types 2 and 3; see Section 7.10) to stay within the pavement strength; the load per wheel is restricted by distributing the total over several wheels. Various arrangements for more than one wheel per strut style are shown in Figure 7.11. Aircraft and undercarriage designers must plan for the number of struts, number of wheels per strut, and tire spacing and pressure (which determine the size) to distribute the load. As the aircraft MTOM increases, so does the number of wheels required, as well as considerations for stowing and articulation for retraction.
The fundamental wheel arrangements are single, twin, triple, and quadruple on a bogey. Wheel arrangements higher than a quadruple are not seen. The next level is their placement in a dual row as a single tandem, twin tandem (i.e., four wheels), triple tandem (i.e., six wheels), and so forth. The A380 wheel-arrangement model is shown in Figure 7.11. Figure 7.1 shows the wheel bogey of the world’s largest aircraft (i.e., the Antanov 225) with twin wheels per strut, for a total of seven struts.
7.9 Loads on Wheels and Shock Absorbers
In its elementary representation, the undercarriage system acts as a spring-mass system, shown in Figure 7.12. Shock absorption is accomplished by its main spring and, to a smaller extent, by the tire pneumatics. Both spring and tire deflect under load. The oleo system acts as a damper; that is, it dissipates kinetic energy of vertical velocity. The strut can act as a spring for the lateral load of the ground friction.
The length of the strut is influenced by the extent that its shock absorber is compressed to the maximum. The minimum strut length is when both tire and shock
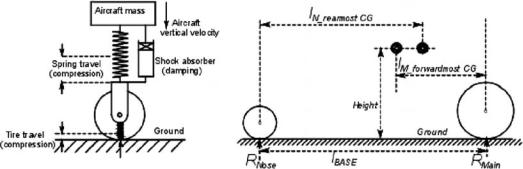
7.9 Loads on Wheels and Shock Absorbers |
203 |
Figure 7.12. Undercarriage as a spring-mass system
absorber collapse simultaneously, yet provide sufficient ground clearance for flaps fully extended (see Figure 7.8). The most critical situation for flap clearance is when the main wheel has collapsed and the nose wheel is at the fully extended position. (In a practical situation, the nose wheel tire would also remain deflected under load, but the margin of the fully extended position is safer.) The flap trailing edge is at its lowest at aircraft rotation for liftoff. A simultaneous failure of the tire and shock absorber after decision speed V1 (see Chapter 13) would force the pilot to continue with the aircraft rotation and liftoff.
During landing, as lift is depleting with speed reduction, more aircraft weight is reacting at the ground contact, which increases the spring load of the strut. The energy is stored in the spring. On brake application, the kinetic energy of the aircraft is absorbed by the brake pads, increasing temperature. If the limits are crossed with rapid deceleration, a fire hazard exists.
7.9.1 Load on Wheels
The load on the wheels determine the tire size. Wheel load is the aircraft weight distributed over the number of wheels. The aircraft CG position could vary depending on the extent of payload and fuel-load distribution; therefore, both the forwardmost and aftmost CG positions must be considered. (Table 7.4 provides an idea of the A380 load.)
As soon as the preliminary undercarriage information is known from the methodology described in this chapter, aircraft weights and the CG can be estimated through the formal procedure described Chapter 8.
Estimating the aftmost CG with the angle β ≈ 15 coinciding with 40% of the MAC gives a preliminary idea of the main-wheel position relative to the wing. The wing position relative to the fuselage could change when the formal weight and CG estimations are determined after the wing is sized. In that case, the wheel-load calculation must be revised. For transport aircraft design, at this stage, the forwardmost CG is 20 to 25% of the MAC ahead of the aftmost CG. For the nontransport category, including combat aircraft design, at this stage the forwardmost CG is 15% of the MAC ahead of the aftmost CG. The MTOW rather than the MTOM is used in the computation because the load is a force. (A simplified approach is to divide the mainand nose-wheel loads as 90 and 10% distribution, which has a

204 |
Undercarriage |
reasonable result, but the author recommends making the formal estimation at the beginning.)
Linear distance is represented by l with associated subscripts; R represents reaction forces. For more than one wheel, the load would then be divided accordingly. The force balance gives:
MTOW = 2 × RMAIN + RNOSE |
(7.1) |
To compute the maximum main-wheel load at the aftmost CG position, take the moment about the nose wheel. The moment equilibrium equation becomes:
lBASE × RMAIN = lN REAR CG × MTOW |
|
or RMAIN = (lN REAR CG × MTOW)/ lBASE |
(7.2) |
The load per strut on the main wheel is: |
|
LM = RMAIN /number of struts |
(7.3) |
To compute the maximum nose-wheel load at the forwardmost CG position, take the moment about the main wheel. The moment equilibrium equation becomes:
lBASE × RNOSE = lM FORWARD CG × MTOW |
|
or RNOSE = (lM FORWARD CG × MTOW)/ lBASE |
(7.4) |
The nose wheel typically has one strut.
Ensure that the load at the nose gear is not too high (i.e., no more than 20% of the MTOW) to avoid a high elevator load to rotate the aircraft for liftoff at takeoff. Also, it must not be too low – that is, not less than 8% of the MTOW; otherwise, there could be steering problems.
For more than one wheel per strut, the load per tire is calculated based on what each tire would produce on the same runway pavement stress at the same tire pressure as a single wheel. This is the equivalent single wheel load (ESWL) because loads are not shared equally when arranged side by side, unlike tandem arrangements. Wheel arrangements determine the ESWL as given here based on statistical means. Readers may consult the references for more details on other types of wheel arrangements.
The tandem twin wheel is:
ESWL = load per strut/2 |
(7.5) |
The side-by-side twin wheel is:
ESWL = load per strut/(1.5 to 1.33) (this book uses 1.5) |
(7.6) |
The tandem triple wheel is:
ESWL = load per strut/3 |
(7.7) |
The side-by-side triple wheel is:
ESWL = load per strut/(1.5 to 1.33) (this book uses 1.5) |
(7.8) |

7.9 Loads on Wheels and Shock Absorbers |
205 |
Table 7.1. Vertical speed |
|
|
|
|
|
VVert, = < 12 fps – FAR 23 (semi-empirical formula for exact rate, nl = 3) |
|
VVert, = < 12 fps – FAR 25 (nl = 2) |
|
VVert, = < 10 fps – Military transport (nl = 2) |
|
VVert, = < 13 fps – Military trainer (nl = maximum 5) |
|
VVert, = < 17 fps – Military land-based combat aircraft (nl = maximum 6) |
|
VVert, = < 22 fps – Military naval (aircraft-carrier)–based combat aircraft (nl = 8) |
|
The twin tandem is |
|
ESWL = load per strut/(3 to 2.67) |
(7.9) |
The main-wheel loads are calculated based on the aftmost CG position and the nosewheel loads are based on the forwardmost CG position. The dynamic load on the wheel is 50% higher than the static load.
7.9.2 Energy Absorbed
Both the tire and the shock absorber absorb the energy to cushion the impact of an aircraft’s vertical descent rate at landing in order to maintain structural integrity and avoid the tire bottoming out. FAA safety requirements limit the vertical descent velocity, VVert, for civil aircraft applications; military specifications limit military applications. Table 7.1 lists limits for various types of aircraft. In turn, VVert produces g-load at the sudden termination of VVert at landing – it can be expressed as load factor n (see Section 5.5). Equation 5.4 gives n = (1 + a/g); it is loosely termed as the number of the g-load; for an undercarriage design, it is designated n1 (see Table 7.1). During landing, nl takes a positive value; that is, it would experience heavier weight. For example,
nl = x (a number) means that the weight has changed by x times. |
(7.10) |
These are extreme values for safety; in practice, 4 fps is a hard landing in a civil aircraft operation. The maximum landing aircraft mass ML is taken as 0.95 MTOM for aircraft with a high wing-loading.
The vertical velocity kinetic energy to be absorbed is
Eab = 1/2ML × VVert |
2 |
(7.11) |
|
This is the energy to be absorbed by all the main wheels (m wheels) and struts (n struts) at touchdown during landing. The nose wheel touches the ground much later, after the main wheels have already absorbed the impact of landing.
Eab = Eab strut + Eab tire |
(7.12) |
ENERGY ABSORPTION BY STRUT (Let n be the number of struts.)
Assume that a landing is even and all struts have equal deflection of δstrut. Then, energy absorbed by all the struts is
Eab strut = n × nl × gML × kstrut × δstrut, |
(7.13) |
where kstrut is an efficiency factor representing the stiffness of the spring and has values between 0.5 and 0.8, depending on the type of shock absorber used.

206 |
Undercarriage |
In this book, 0.7 is used for modern aircraft and 0.5 is used for small club and homebuilt categories.
ENERGY ABSORPTION BY TIRE (Let m be the number of tires.)
Assume that a landing is even and all tires have equal deflection of δtire. Then, energy absorbed by all the tires is
Eab tire = m × nl × gML × ktire × δtire |
(7.14) |
where ktire = 0.47 is an efficiency factor representing the stiffness of all types of tires.
The following can be written by equating Equation 7.11 with Equation 7.12 and then substituting Equations 7.13 and 7.14 in Equation 7.12 and replacing nl by Equation 7.10. Here, the load factor nl is replaced by x:
Eab = 1/2ML × VVert2 = n × x × gML × kstrut × δstrut + m × x × gML × ktire × δtire
Simplifying as follows:
1/2 × VVert2 /g = x×(n × kstrut × δstrut + m × ktire × δtire) |
(7.15) |
7.9.3 Deflection under Load
The total vertical deflection of the strut and tire during landing can be computed by using Equation 7.15. Other types of lateral strut deflection during turning and other maneuvers are not addressed in this book.
Total deflection is
δ = δstrut + δtire |
(7.16) |
It is recommended that a cushion be kept in the strut deflection (compression) so that ends do not hit each other. In general, 1 inch (2.54 cm) is the margin.
7.10 Runway Pavement Classification
The undercarriage design depends on how the wheels interact with the airfield surface. An airport runway surface must be designed to withstand an aircraft’s weight not only at the static condition but also at dynamic loading (e.g., for a heavy landing). Runway pavement loading is known as flotation. Among airports, the runway pavement strength varies. There are three main types of surfaces, as follows:
1.Type 1: Unprepared Surface. A grass field or a gravel field, for example, is designated as a Type 1 surface. These are soft runways that are prone to depressions under a heavy load. Low-pressure tires with a maximum 45 to 60 lb per square inch (psi) and a total ESWL load less than 10,000 lb are the limits of operation on a soft runway. The ground friction is the highest and these airfields are not necessarily long. This type of runway is the least expensive to prepare and they serve remote areas, as an additional airfield close to a business center, or as a private airfield. Small utility aircraft can operate from Type 1 airfields.
7.10 Runway Pavement Classification |
|
|
207 |
|||
Table 7.2. Load classification group |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
LCN range |
LCG |
LCN range |
LCG |
LCN range |
LGG |
|
|
|
|
|
|
|
|
101 to 120 |
I |
31 to 50 |
IV |
11 to 15 |
VI |
|
76 to 100 |
II |
16 to 30 |
V |
10 and below |
VII |
|
51 to 75 |
III |
|
|
|
|
|
|
|
|
|
|
|
|
2.Type 2: Prepared Macadam Surface. These are asphaltor tar-topped runways with strength built in by the thick macadam filler; these are designated as a Type 2 surface. These surfaces are less expensive to prepare by using a heavily rolled macadam filler. However, local depressions can cause the surface to undulate, and it requires frequent maintenance with longer downtime. This type of runway can accommodate heavy aircraft such as the B747.
3.Type 3: Prepared Concrete Surface. This is a rigid concrete runway designated as a Type 3 surface. These runways are built with pavement-quality concrete (i.e., about a half-meter thick) and are covered by asphalt (e.g., 150 mm thick). All major international airports have Type 3 runways, which can take a load similar to a Type 2 surface and do not have to be as thick. This type is expensive to prepare and maintenance downtime is minimal. Cracks are the typical type of failure that occurs. A Type 3 surface can accommodate heavy aircraft such as the B747 and the A380.
Aircraft designers must design aircraft to be compatible with existing airfields in order to operate. If the market demand necessitates larger and heavier aircraft, then designers must make the aircraft comply with the pavement strength of existing airfields or the airfield must be reinforced to accept the heavy aircraft. Runway reinforcement depends on new designs; therefore, airport authorities communicate with aircraft manufacturers to remain current with market demand. When the B747 began operating, almost all international airfields needed reinforcement to accept them – some were not operational for several years.
7.10.1 Load Classification Number Method
The ICAO, as an international agency, established ground rules to match aircraft and runway performance requirements. The ICAO developed the strength classifications of Type 2 and Type 3 runways by designating a load classification number (LCN) that represents the extent of load that a runway can accommodate based on construction characteristics. All Type 2 and Type 3 runways must have a LCN and the aircraft undercarriage design must comply with it. The LCN range of the airfield’s type is grouped under the load classification group (LCG). For example, an aircraft with the LCN 62 can operate on any airfield with an LCG of I to III. Table 7.2 provides the LCN range for the types of runways.
The relationship among the LCN, tire pressure, and ESWL is presented in Figure 7.13. The procedure is to first obtain the LCN of the airfield in question. Then, compute the ESWL of the undercarriage (see Section 7.9). Finally, find the tire pressure required using Table 7.6 (see Section 7.11); this provides a guideline to choose tire size. Section 7.13 outlines the methodology followed by worked-out
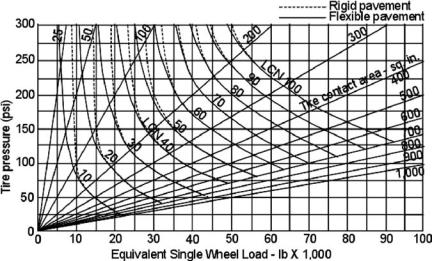
208 |
|
|
|
Undercarriage |
|
|
Table 7.3. Aircraft weight to comply with LCN and corresponding tire pressure |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Aircraft |
MTOM (lb) |
Tire pressure (psi) |
LCN |
|
|
|
|
|
|
|
|
Fokker F27 |
45,000 |
80 |
19 |
|
|
McDonnell DC-9 |
65,000 |
129 |
39 |
|
|
B737–200 |
110,000 |
162 |
49 |
|
|
B757 |
210,000 |
157 |
50 |
|
|
B707 |
300,000 |
180 |
80 |
|
|
|
|
|
|
|
examples (see the references for more details on other types). Typical examples of aircraft complying with the LCN and the corresponding MTOM and tire pressures are given in Table 7.3.
The B757, which is twice as heavy as the B737, maintains nearly the same LCN by having more wheels to distribute load per tire.
7.10.2 Aircraft Classification Number and Pavement
Classification Number Method
The LCN is airfield-specific and aircraft must comply with it. Subsequently, ICAO introduced a new classification system, known as the aircraft classification number (ACN), which represents the tire-loading limit, and another system that represents the airfield pavement-strength limit, known as the pavement classification number (PCN). Both numbers must be the same to operate at an airport without any restrictions. However, the LCN method is still in use and conversion is needed to use the ACN/PCN method. This book uses Figure 7.13 to obtain the LCN.
The ACN/PCN method is described in [9]. According to the design manual, the ACN/PCN method is intended only for publication of pavement-strength data in the Aeronautical Information Publication (AIP). It is not intended for design or
Figure 7.13. Equivalent single-wheel load versus LCN
